GBDT模型 0基础小白也能懂(附代码)
GBDT模型 0基础小白也能懂(附代码)
啥是GBDT
GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,是一种迭代的决策树算法,又叫 MART(Multiple Additive Regression Tree),它通过构造一组弱的学习器(树),并把多颗决策树的结果累加起来作为最终的预测输出。该算法将决策树与集成思想进行了有效的结合。
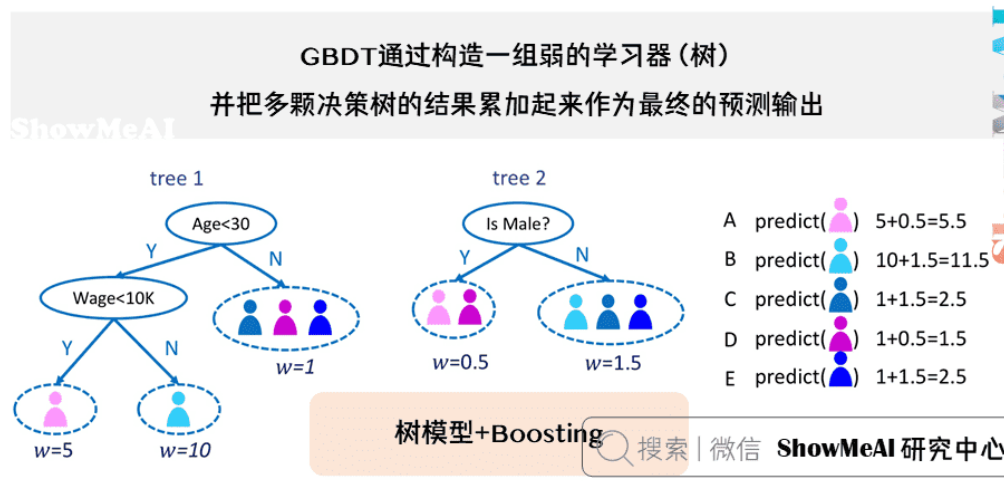
Gradient Boosting里的boosting是啥?
Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重(并根据前一个基分类器的表现计算误差。对于分类正确的样本,它们的权重保持不变或减少;对于分类错误的样本,算法会增加它们的权重)。测试时,根据各层分类器的结果的加权得到最终结果。
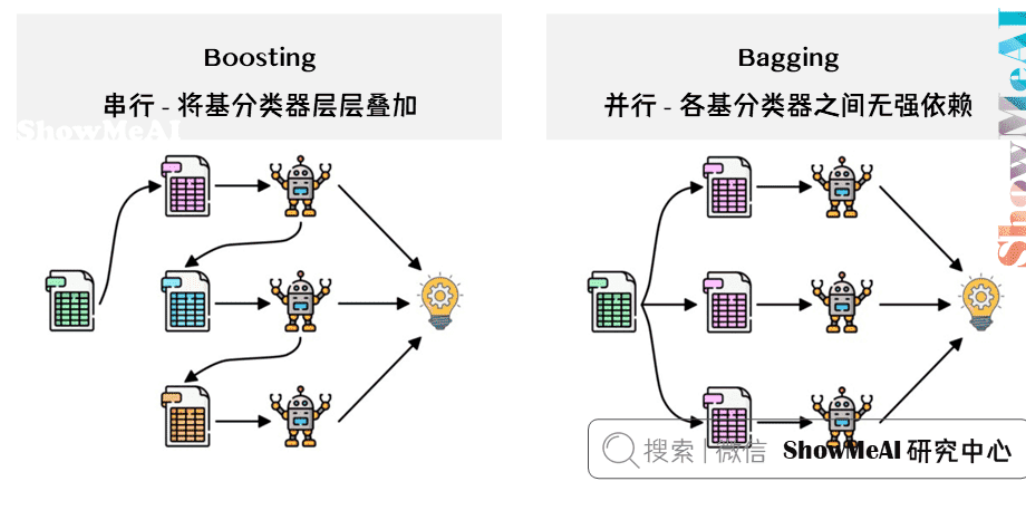
Bagging 与 Boosting 的串行训练方式不同,Bagging 方法在训练过程中,各基分类器之间无强依赖,可以进行并行训练。
GBDT详解
所有弱分类器的结果相加等于预测值。
每次都以当前预测为基准,下一个弱分类器去拟合误差函数对预测值的残差(预测值与真实值之间的误差)。
GBDT的弱分类器使用的是树模型。
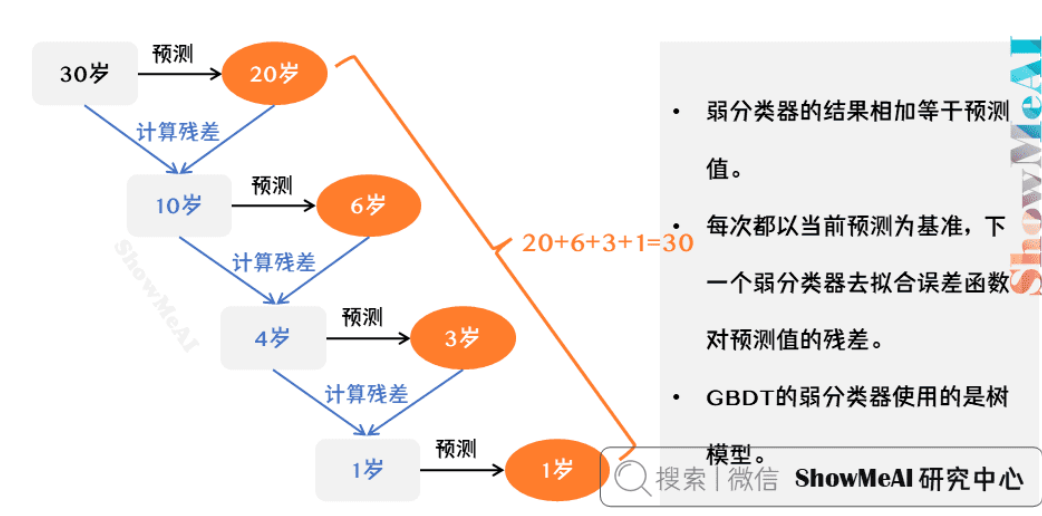
实际工程实现里,GBDT 是计算负梯度,用负梯度近似残差,而不是像这样简单相减
1)GBDT与负梯度近似残差
回归任务下,GBDT在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数:

可以看出,当损失函数选用「均方误差损失」时,每一次拟合的值就是(真实值-预测值),即残差。
2)GBDT训练过程
我们来借助1个简单的例子理解一下 GBDT 的训练过程。假定训练集只有4个人\(A,B,C,D\),他们的年龄分别是\((14,16,24,26)\)。身份分别是高一学生,高三学生,应届毕业生,已工作两年。为了按照特征预测年龄
先用回归树训练后看结果,里面分的节点只是例子,没啥具体含义,先按购物金额分一下,再按上网时间或者上网时段分一下
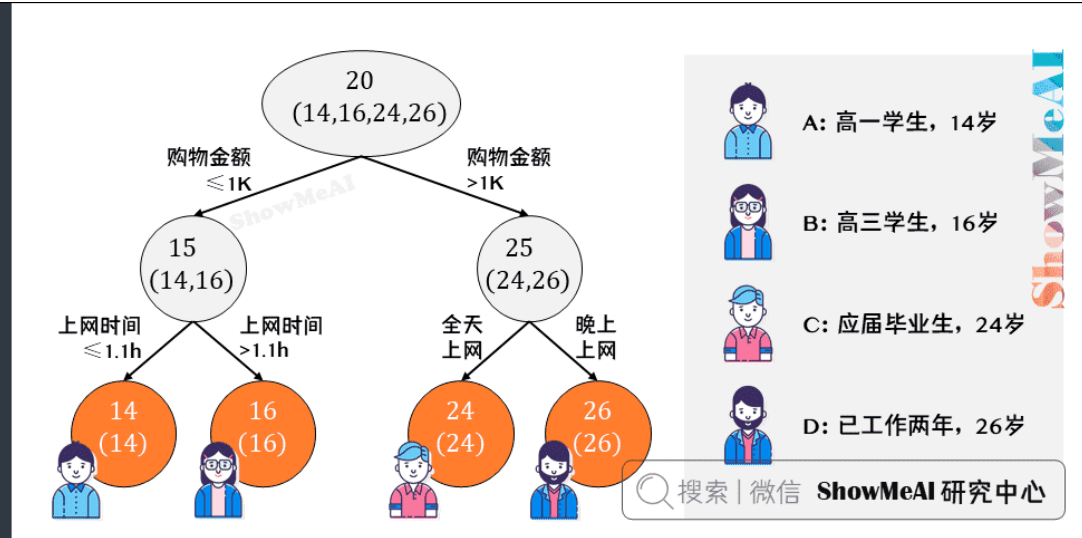
接下来改用 GBDT 来训练。由于样本数据少,我们限定叶子节点最多为2即每棵树都只有一个分枝),并且限定树的棵树为2。先按照购物金额来分出一棵树:
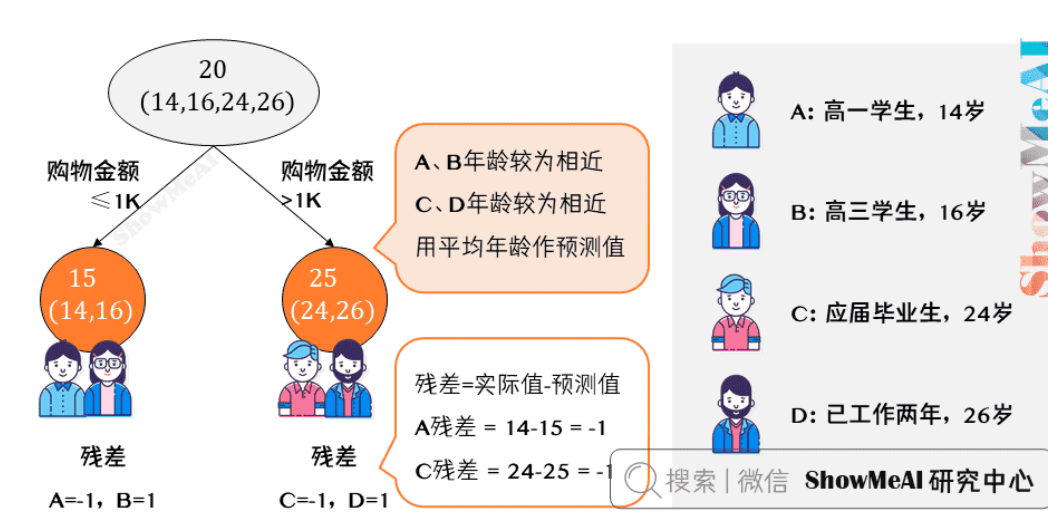
上图中的树很好理解:\(A,B\) 年龄较为相近,\(C,D\) 年龄较为相近,被分为左右两支,每支用平均年龄作为预测值。
- 我们计算残差(即「实际值」-「预测值」),所以\(A\)的残差 \(15-1=14\)。
- 这里 \(A\) 的「预测值」是指前面所有树预测结果累加的和,在当前情形下前序只有一棵树,所以直接是 \(15\),其他多树的复杂场景下需要累加计算作为 \(A\) 的预测值。
那么到这里预测完成,接下来就是要用一个弱分类器(树)去拟合误差函数对预测值的残差(预测值与真实值之间的误差)
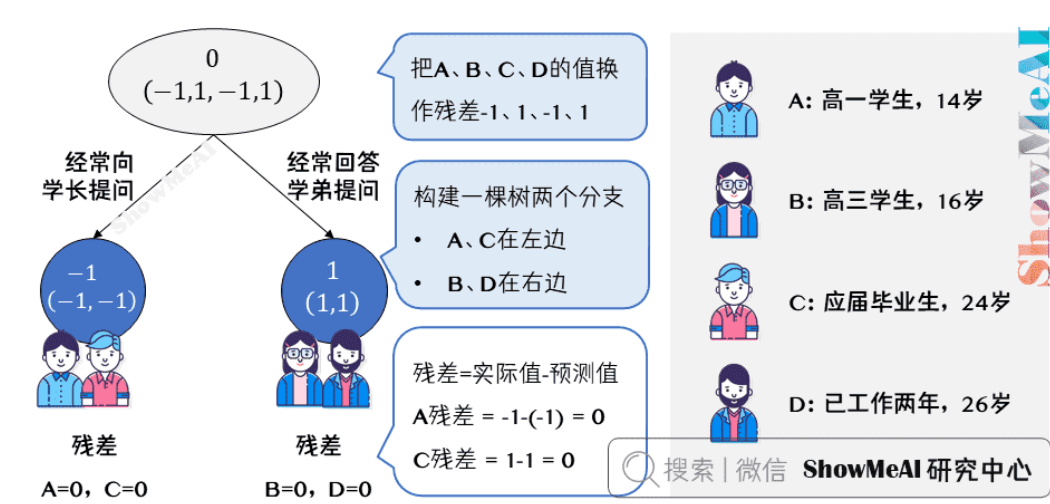
上图中的树就是残差学习的过程了,里面提问和回答同样也只是例子:
- 把 \(A,B,C,D\) 的值换作残差 \(-1,1,-1,1\),再构建一棵树学习,这棵树只有两个值 \(1\) 和 \(-1\),直接分成两个节点:\(A,C\) 在左边,\(B,D\) 在右边。
- 这棵树学习残差,在我们当前这个简单的场景下,已经能保证预测值和实际值(上一轮残差)相等了。
- 我们把这棵树的预测值累加到第一棵树上的预测结果上,就能得到真实年龄,这个简单例子中每个人都完美匹配,得到了真实的预测值。
最终的预测过程是这样的:
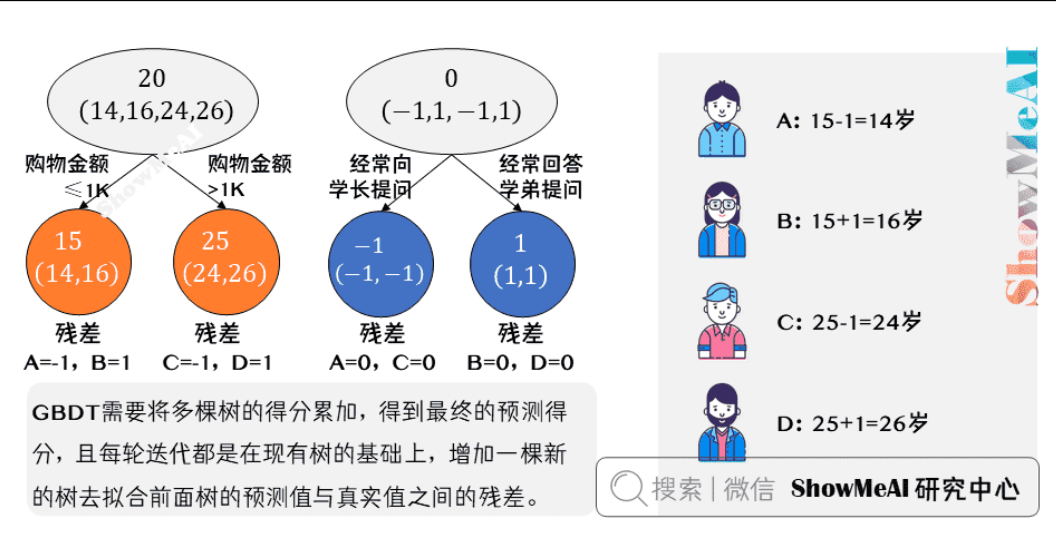
- \(A\):高一学生,购物较少,经常问学长问题,真实年龄 14 岁,预测年龄 15-1
- \(B\):高三学生,购物较少,经常被学弟提问,真实年龄 16 岁,预测年龄 15+1
- \(C\):应届毕业生,购物较多,经常问学长问题,真实年龄 24 岁,预测年龄 25-1
- \(D\):工作两年员工,购物较多,经常被学弟提问,真实年龄 26 岁,预测年龄 25+1
综上,GBDT 需要将多棵树的得分累加得到最终的预测得分,且每轮迭代,都是在现有树的基础上,增加一棵新的树去拟合前面树的预测值与真实值之间的残差。
梯度提升 vs 梯度下降
下面我们来对比一下「梯度提升」与「梯度下降」。这两种迭代优化算法,都是在每1轮迭代中,利用损失函数负梯度方向的信息,更新当前模型,只不过:
梯度提升(比如前面的GBDT):通过构建多个弱学习器,在函数空间中逼近最优解,不需要模型参数化,利用损失函数的负梯度逐步优化模型。
梯度下降(比如线性回归,逻辑回归):通过参数化的模型,利用损失函数的梯度更新参数,最终找到使损失最小的参数。
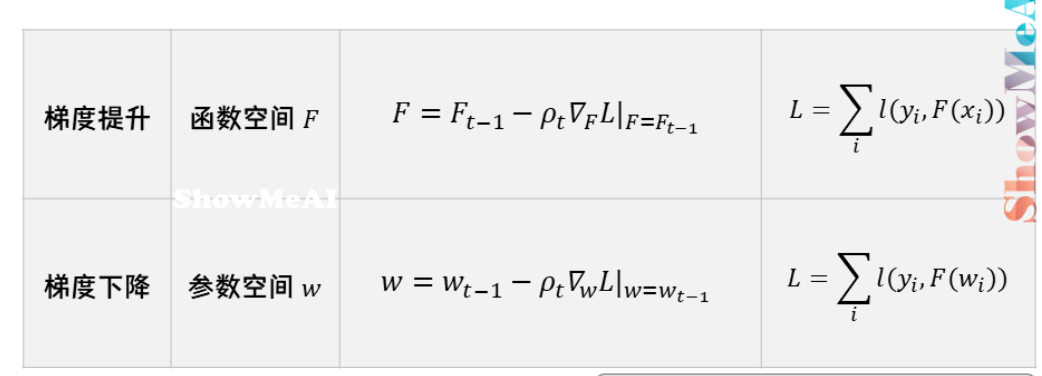
优缺点

随机森林 vs GBDT

何时使用哪个模型?
使用随机森林:如果你需要快速构建一个可用的模型,并且数据量较大,可以考虑使用随机森林。它对参数的敏感性较低,容易调参,适用于初步探索。
使用GBDT:如果你在追求更高的模型精度,尤其是在较复杂的数据集上,GBDT 通常表现更好,但需要更多的时间来调整超参数。
代码实现
还是用加州房价数据集
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error, r2_score
# 1. 加载加州房价数据集
data = fetch_california_housing()
X = data.data # 特征矩阵
y = data.target # 目标变量(房价)
# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 3. 创建GBDT回归模型
# n_estimators: 基分类器的数量
# learning_rate: 每个基分类器的学习率
# max_depth: 决策树的最大深度
gbdt_regressor = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)
# 4. 训练模型
gbdt_regressor.fit(X_train, y_train)
# 5. 进行预测
y_pred_train = gbdt_regressor.predict(X_train)
y_pred_test = gbdt_regressor.predict(X_test)
# 6. 评估模型
# 计算测试集的均方误差
mse_test = mean_squared_error(y_test, y_pred_test)
print(f"Mean Squared Error (Test): {mse_test:.2f}")
# 计算训练集的均方误差
mse_train = mean_squared_error(y_train, y_pred_train)
print(f"Mean Squared Error (Train): {mse_train:.2f}")
# 计算R²得分
r2_test = r2_score(y_test, y_pred_test)
r2_train = r2_score(y_train, y_pred_train)
print(f"R² Score (Test): {r2_test:.2f}")
print(f"R² Score (Train): {r2_train:.2f}")
# 7. 可视化GBDT的预测结果(实际值 vs. 预测值)
plt.scatter(y_test, y_pred_test, alpha=0.5)
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.title('Actual vs Predicted Prices (GBDT)')
plt.show()
结果如下
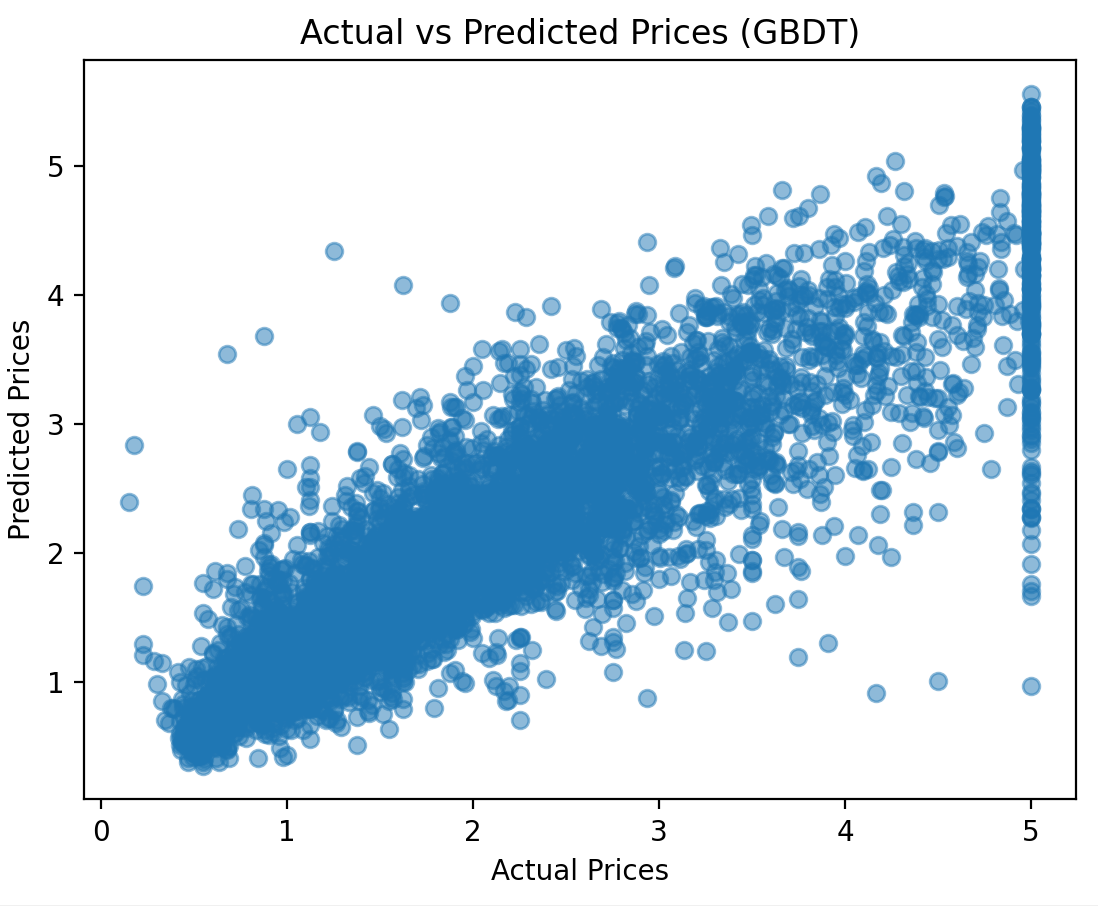
Mean Squared Error (Test): 0.29
Mean Squared Error (Train): 0.26
R² Score (Test): 0.78
R² Score (Train): 0.81
和我们之前的决策树相比明显好了很多,毕竟这里数据规模不大。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号