[noip2016] 蚯蚓 (队列)
Description

Input

Output

Sample Input
样例1:
3 7 1 1 3 1
3 3 2
样例2:
3 7 1 1 3 2
3 3 2
样例3:
3 7 1 1 3 9
3 3 2
Sample Output
样例1:
3 4 4 4 5 5 6
6 6 6 5 5 4 4 3 2 2
样例2:
4 4 5
6 5 4 3 2
样例3:
//空行
2
HINT

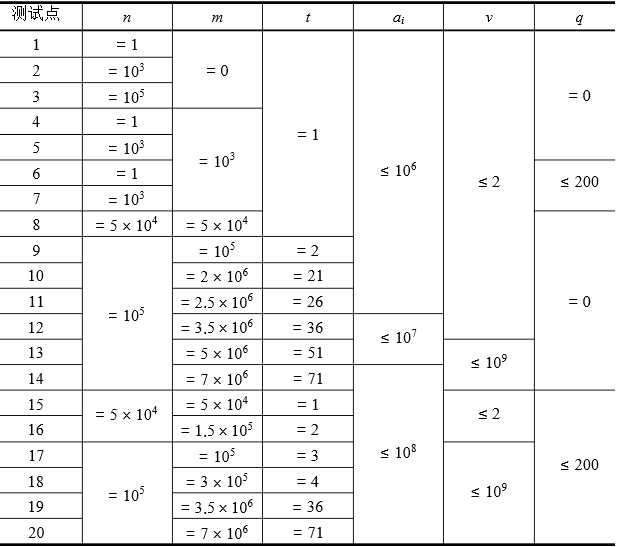
Solution
很显然是一道优先队列的题0_0
我们每次拿出最大的一只蚯蚓切割再扔到堆里(第一问)
然后将堆中的东西依次取出(第二问)
那怎么将堆中蚯蚓每次加上q呢?
可以设一个变量表示当前蚯蚓已经被加了多少,出队时加上就行(入队时记得减去)
那切割后的蚯蚓不增加q怎么办?那就入队时先-q就行了
然后这样\(O((n+m)log(n+m))\)就应该可以水过很多分了~
然后说正解:其实正解也是跟上面一样的步骤只不过证明了一个单调性,省去log(n+m)的时间
证明:后分解出的⌊px⌋一定小于先分解出的⌊px⌋ (x-⌊px⌋同理)
考虑反证法若\(xi*p+(j-i)*q<=(xj+(j-i)*q)*p\)
则有:\(xi*p+(j-1)*q<=xj*p+(j-i)*q*p\)
因为\(xi>xj\)且\(0<p<1\)该式显然不成立
说明⌊px⌋单调递减成立
有了单调性我们就可以用三个队列模仿优先队列一样操作
时间复杂度:\(O(nlogn+m)\)
Code
//By Menteur_Hxy
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define F(i,a,b) for(register int i=(a);i<=(b);i++)
using namespace std;
int read() {
int x=0,f=1; char c=getchar();
while(!isdigit(c)) {if(c=='-')f=-f;c=getchar();}
while(isdigit(c)) x=(x<<1)+(x<<3)+c-48,c=getchar();
return x*f;
}
const int INF=0x7fffffff;
const int N=1e5+10,M=7e6+10;
int n,m,q,u,v,t,reg;
int Q[3][M],qt[3],qf[3];
bool cmp(int x,int y) {return x>y;}
int Max() {
int res=-INF,cnt;
F(i,0,2) if(qf[i]<qt[i]&&res<Q[i][qf[i]+1])
res=Q[i][qf[i]+1],cnt=i;
qf[cnt]++; return res;
}
int main() {
n=read(),m=read(),q=read(),u=read(),v=read(),t=read();
F(i,1,n) Q[0][++qt[0]]=read();
sort(Q[0]+1,Q[0]+qt[0]+1,cmp);
F(i,1,m) {
int x=Max()+reg;
if(i%t==0) printf("%d ",x);
int l=(long long)x*u/v,r=x-l;
Q[1][++qt[1]]=l-reg-q;
Q[2][++qt[2]]=r-reg-q;
reg+=q;
}
putchar('\n');
F(i,1,n+m) {
int x=Max()+reg;
if(i%t==0) printf("%d ",x);
}
return 0;
}
版权声明:本文为博主原创文章,未经博主允许不得转载。
博主:https://www.cnblogs.com/Menteur-Hxy/

