[luogu1600 noip2016] 天天爱跑步 (树上差分)
题目描述
小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一一棵包含 n个结点和 n−1 条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从 1 到 n 的连续正整数。
现在有 m 个玩家,第 i 个玩家的起点为 Si ,终点为 Ti 。每天打卡任务开始时,所有玩家在第 0 秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)
小c想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点 j 的观察员会选择在第 Wj 秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第 Wj 秒也理到达了结点j 。 小C想知道每个观察员会观察到多少人?
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点 jjj 作为终点的玩家: 若他在第 WjW_jWj 秒前到达终点,则在结点 j的观察员不能观察到该玩家;若他正好在第 Wj 秒到达终点,则在结点 j 的观察员可以观察到这个玩家。
输入输出格式
输入格式:
第一行有两个整数 n 和 m 。其中 n 代表树的结点数量, 同时也是观察员的数量, m 代表玩家的数量。
接下来 n−1 行每行两个整数 u 和 v ,表示结点 u 到结点 v 有一条边。
接下来一行 n 个整数,其中第 j 个整数为 Wj , 表示结点 j 出现观察员的时间。
接下来 m 行,每行两个整数 Si,和 Ti ,表示一个玩家的起点和终点。

输出格式:
输出1行 n 个整数,第 j个整数表示结点 j 的观察员可以观察到多少人。
输入输出样例
输入样例#1:
6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6
输出样例#1:
2 0 0 1 1 1
输入样例#2:
5 3
1 2
2 3
2 4
1 5
0 1 0 3 0
3 1
1 4
5 5
输出样例#2:
1 2 1 0 1
说明

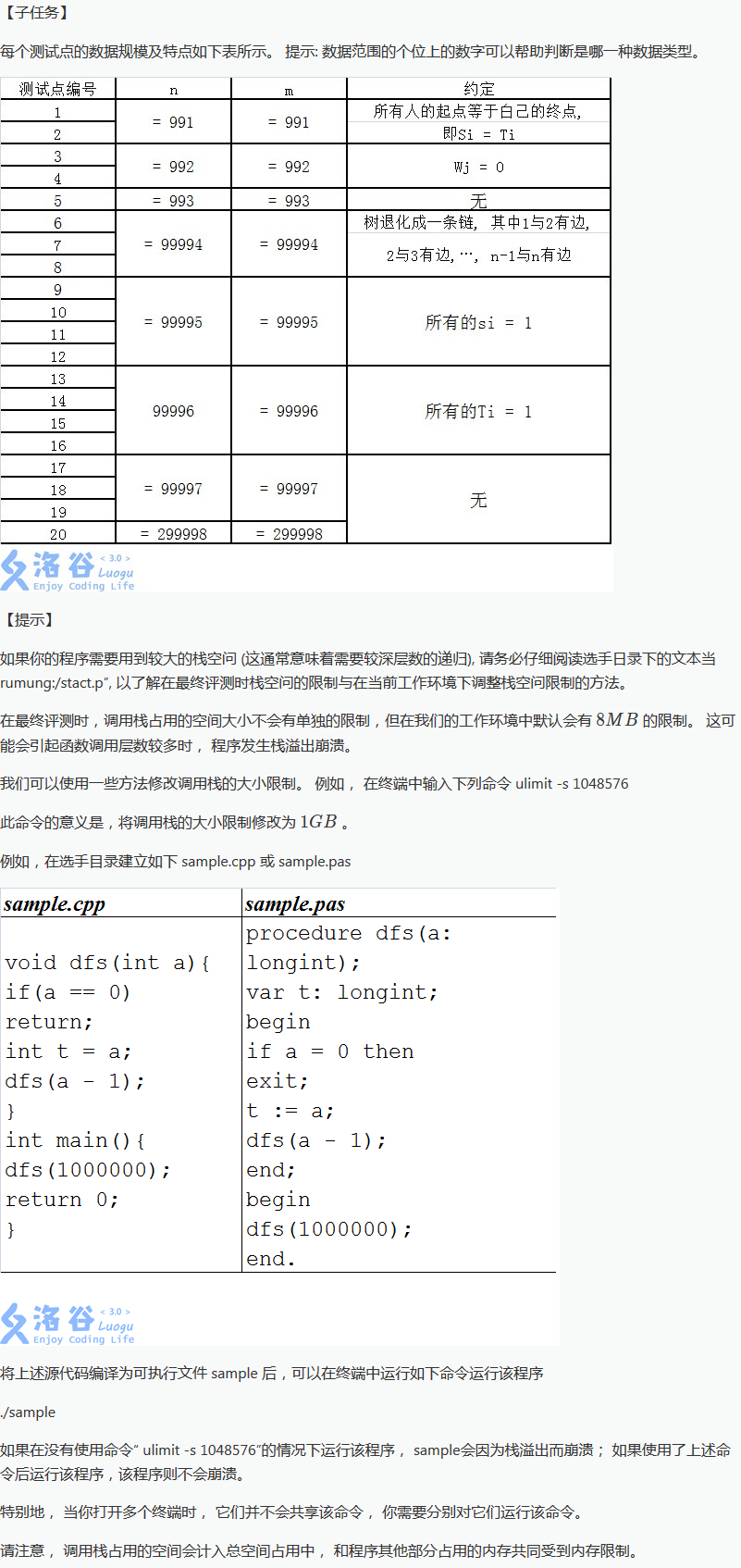
题解:
树上差分,暂且留坑
code:
//By Menteur_Hxy
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#define M(a,b) memset(a,(b),sizeof(a))
#define F(i,a,b) for(register int i=(a);i<=(b);i++)
#define E(i,u) for(register int i=head[u];i;i=nxt[i])
#define _E(i,u) for(register int i=_head[u];i;i=_nxt[i])
#define V(it,a) for(vector<int>::iterator it=a.begin();it!=a.end();it++)
using namespace std;
int rd() {
int x=0,f=1; char c=getchar();
while(!isdigit(c)) {if(c=='-')f=-f; c=getchar();}
while(isdigit(c)) x=(x<<3)+(x<<1)+c-48,c=getchar();
return x*f;
}
const int N=600010;
int n,m,cnt,md;
int nxt[N],head[N],to[N],w[N],fa[N],dep[N],num[N],vis[N];
int _cnt,_nxt[N],_head[N],_to[N];
struct players{int s,t,lca,dis;}pl[N];
int getf(int x) {return fa[x]==x?x:fa[x]=getf(fa[x]);}
void tarjan(int u,int pre) {
vis[u]=1; dep[u]=dep[pre]+1;
_E(i,u) { int v=_to[i];
if(pl[v].s==u&&vis[pl[v].t]) pl[v].lca=getf(pl[v].t);
if(pl[v].t==u&&vis[pl[v].s]) pl[v].lca=getf(pl[v].s);
// cout<<pl[v].s<<" "<<pl[v].t<<" "<<pl[v].lca<<" "<<u<<endl;
}
E(i,u) { int v=to[i];
if(v==pre) continue;
tarjan(v,u);
fa[v]=u;
if(dep[v]>md) md=dep[v];
}
}
vector <int> t1[N],t2[N],t3[N];
int tu[N],td[N<<1],ans[N];
void dfs(int u,int pre) {
int a=td[dep[u]+w[u]],b=tu[dep[u]-w[u]+N];
td[dep[u]]+=num[u];
V(i,t1[u]) tu[*i+N]++;
E(i,u) if(to[i]!=pre) dfs(to[i],u);
ans[u]=td[dep[u]+w[u]]-a+tu[dep[u]-w[u]+N]-b;
V(i,t2[u]) {td[*i]--; if(*i==dep[u]+w[u]) ans[u]--;}
V(i,t3[u]) tu[*i+N]--;
}
#define _add(a,b) _nxt[++_cnt]=_head[a],_to[_cnt]=b,_head[a]=_cnt;
#define add(a,b) nxt[++cnt]=head[a],to[cnt]=b,head[a]=cnt
int main() {
n=rd(),m=rd();
F(i,1,n-1) {int a=rd(),b=rd(); add(a,b);add(b,a);}
F(i,1,n) w[i]=rd(),fa[i]=i;
F(i,1,m) {pl[i].s=rd(),pl[i].t=rd(),num[pl[i].s]++;
// cout<<pl[i].s<<" "<<pl[i].t<<" "<<i<<endl;
_add(pl[i].s,i);_add(pl[i].t,i);}
tarjan(1,0);
// for(int i=1;i<=n;i++) cout<<pl[i].lca<<" ";cout<<endl;
F(i,1,m) {
pl[i].dis=dep[pl[i].s]+dep[pl[i].t]-(dep[pl[i].lca]<<1);
t2[pl[i].lca].push_back(dep[pl[i].s]);
t3[pl[i].lca].push_back(dep[pl[i].t]-pl[i].dis);
t1[pl[i].t].push_back(dep[pl[i].t]-pl[i].dis);
// cout<<dep[pl[i].s]<<" "<<dep[pl[i].t]<<" "<<dep[pl[i].lca]<<" "<<pl[i].dis<<" "<<endl;
}
dfs(1,0);
for(int i=1;i<=n;i++) printf("%d ",ans[i]);
return 0;
}

