Codeforces962F Simple Cycles Edges 【双连通分量】【dfs树】

题目大意：

　　给出一个无向图，问有哪些边只属于一个简单环。

题目分析：

　　如果这道题我们掌握了点双连通分量，那么结论会很显然，找到每个点双，如果一个n个点的点双正好由n条边构成，那么这些边都是可以的。

　　这样想显得很没有技术含量，使用一类通用的做法做一些有特点的题目总是不那么锻炼人的思维，但在算法竞赛中我仍然推荐点双的做法。

　　这题很有特点，我们尝试不用点双解决它。

　　首先，考虑一个简单环，它不由几个简单环组合并删去某些边组合而成。它的dfs树的形状将会是这样的：

　　

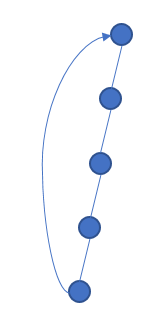
　　其中箭头标注的是返祖边。

　　一个简单环中的所有边被选，当且仅当它唯一的一条返祖边所包括的点不被其它返祖边所覆盖任何一段，但是这一段并不包含仅包含一个点的情况。

　　所以我们可以考虑类似运输计划那样的差分。然后前缀和维护经过的返祖边大于2的边数，这样对每条返祖边判断是O(1)的。所以时间复杂度O(n+m+sort(m))。

代码：

　　

#include<bits/stdc++.h>
using namespace std;

const int maxn = 102000;

#define mp make_pair

int n,m;

struct edge{int from,to;}e[maxn];
vector<pair<int,int> > g[maxn];
int dfn[maxn],f[maxn],dd[maxn],cl,pt[maxn];
int chs[maxn],lnk[maxn];

void read(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
    scanf("%d%d",&e[i].from,&e[i].to);
    g[e[i].from].push_back(mp(e[i].to,i));
    g[e[i].to].push_back(mp(e[i].from,i));
    }
}

vector<int> ans;
vector<int> t[maxn];

void dfs(int now,int fa){
    dfn[now] = ++cl;pt[now] = fa;
    for(int i=0;i<g[now].size();i++){
    pair<int,int> pr = g[now][i];
    if(pr.first == fa) continue;
    if(!dfn[pr.first]){
        t[now].push_back(pr.first);
        chs[pr.second] = 1;lnk[pr.first] = pr.second;
        dfs(pr.first,now);
    }
    else{
        if(dfn[pr.first] > dfn[now]) continue;
        f[now]++; f[pr.first]--;
    }
    }
}

int im[maxn];
void dfs2(int now){
    for(int i=0;i<t[now].size();i++){dfs2(t[now][i]); dd[now]+=dd[t[now][i]];}
    dd[now] += f[now];
}
void dfs3(int now){
    im[now] = im[pt[now]] + (dd[now] > 1);
    for(int i=0;i<t[now].size();i++){dfs3(t[now][i]);}
}

void solve(int now){
    if(dfn[e[now].from] < dfn[e[now].to]) swap(e[now].from,e[now].to);
    int kk = im[e[now].from] - im[e[now].to];
    if(kk == 0){
    int pla = e[now].from;
    while(pla!=e[now].to){ans.push_back(lnk[pla]);pla = pt[pla];}
    ans.push_back(now);
    }
}

void work(){
    for(int i=1;i<=n;i++) { if(!dfn[i]) dfs(i,0),dfs2(i),dfs3(i); }
    for(int i=1;i<=m;i++){ if(!chs[i]) solve(i); }
    sort(ans.begin(),ans.end());
    printf("%d\n",ans.size());
    for(int i=0;i<ans.size();i++){
    printf("%d ",ans[i]);
    }
}

int main(){
    //freopen("1.in","r",stdin);
    //freopen("1.out","w",stdout);
    read();
    work();
    return 0;
}