USACO2023 一月月赛 Platinum 3
Platinum 3
分析
树上的最优化问题先不动脑子DP一波。
用\(f[i]\)表示将以\(i\)为根的子树中，所有子树都满足题设开灭条件所需要的最少次数。
现在把这个子树画成下图这样，假设它有三个儿子\(x_1,x_2,x_3\)
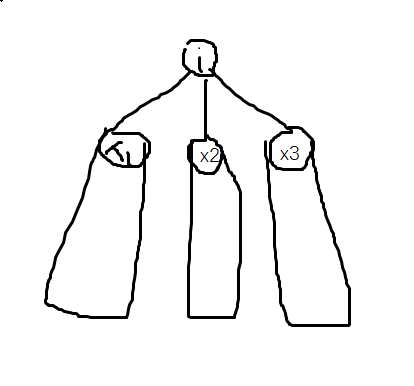
我为了让这一整棵树亮起来，我肯定要在某个时刻是整个树的所有节点都被我打开的，而且最后整个树肯定是会重新变成熄灭的。
对于\(i\)的三个儿子构成的子树\(x_1,x_2,x_3\)，他们有的是在这个树被点亮的过程中被点亮的，有的是在这个树被熄灭的过程中被单独点亮的。
比如，一种可能性是：
...x(x1被点亮).....x(x3被点亮)....x(i被点亮)....x(x2被点亮)
我们注意到，\(x_3\)被点亮的时候，\(x_1\)被完全熄灭了，而且毫无疑问，\(x_3\)被开始点亮前，整个操作序列应该都是\(x_1\)的点亮和熄灭操作。
\(i\)被点亮的时候，我们不应该熄灭\(x_3\)已经被点亮的灯，而是重新点亮\(x_1\)和\(x_2\)。
接着，为了使得\(x_2\)被点亮，我们需要选择熄灭\(x_1\)和\(x_3\)。
接着我们还可以轻易地想到，\(x_1\)的子树中，每个被点亮的点，应当随同\(x_1\)被点亮而点亮，不然的话，来日再点亮就会额外耗费功夫。
在熄灭过程被点亮的儿子子树，数量是不能超过\(1\)个的，如果超过了，那多的可以放前面来。
现在，对于一个有很多儿子\(x_1,...x_k\)的结点\(i\)，令\(f[i]\)表示其满足题目的最小步数，\(g[i]\)表示只点亮\(i\)的所有子树集合的最小步数，不熄灭。
那么，为了点亮\(x_2\)，我需要点亮并熄灭\(x_1\)，花费\(f[x_1]\)次操作，为了点亮\(x_3\)，我需要点亮并熄灭\(x_2\)，以此类推。对于\(x_{k}\)我有两种路子，一种是我点亮\(x_{k}\)，然后点亮\(i\)，熄灭的时候最后留着\(x_{k}\)不熄灭，再按\(f\)顺序熄灭\(x_k\)，这样就是\(f[x_k]\)次操作。另一种路子是我点亮\(x_{k-1}\)，然后点亮\(i\)，熄灭的时候留着\(x_{k}\)不熄灭，按\(g\)顺序的倒序熄灭\(x_k\)，这样就是\(g[x_{k-1}]+g[x_k]\)次操作。
综上，也就是
对于\(g\)的求解，我们枚举一个儿子作为也不熄灭的，可以得到\(g[i]=g[x_k]+\sum f[x_i]+sz[i]-sz[x_k]\)
对于\(f\)，由于我们的枚举，时间复杂度来到了\(O(n^2)\)
对于\(f\)式子左边的这种情况，正常枚举就是\(O(n)\)，我们不需要优化，对于右边的这种情况，相当于我们把两个\(f[x_j]\)换成了\(g[x_j]+sz[i]-sz[x_j]\)，把这个差最大的两个儿子取出来换掉，就是最优的了，所以我们不妨对每个结点，求这两个差的最大值和次大值。
#include<bits/stdc++.h>
using namespace std;
const int maxn=200050;
int fa[maxn];
vector<int> T[maxn];
int sz[maxn];
long long f[maxn],g[maxn];
void dfs(int now){
if(T[now].size() == 0){
f[now] = 2;
g[now] = 1;
sz[now] = 1;
return;
}
long long ans = 0;
f[now] = g[now] = 1e18;
sz[now] = 1;
for(int i=0;i<T[now].size();i++){
dfs(T[now][i]);
ans += f[T[now][i]];
sz[now] += sz[T[now][i]];
}
for(auto x:T[now]){
g[now] = min(g[now],ans-f[x]+g[x]+sz[now]-sz[x]);
f[now] = min(f[now],ans+2*(sz[now]-sz[x]));
}
int big1=0,big2=0,dt1=0,dt2=0;
if(T[now].size() >= 2){
for(auto x:T[now]){
long long dt = f[x]-(g[x]+sz[now]-sz[x]);
if(big1 == 0 || dt >= dt1){
big2 = big1;
dt2 = dt1;
big1 = x;
dt1 = dt;
}else{
if(big2 == 0 || dt >= dt2){
big2 = x;
dt2 = dt;
}
}
}
f[now] = min(f[now],ans-dt1-dt2);
}
}
int main(){
int n; cin >> n;
for(int i=2;i<=n;i++){
cin >> fa[i];
T[fa[i]].push_back(i);
}
dfs(1);
cout<<f[1]<<endl;
}
