代码随想录算法训练营第27天 | 122.买卖股票的最佳时机 II 55. 跳跃游戏 1005.K次取反后最大化的数组和

122.买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。
在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。
返回 你能获得的 最大 利润 。

解题：

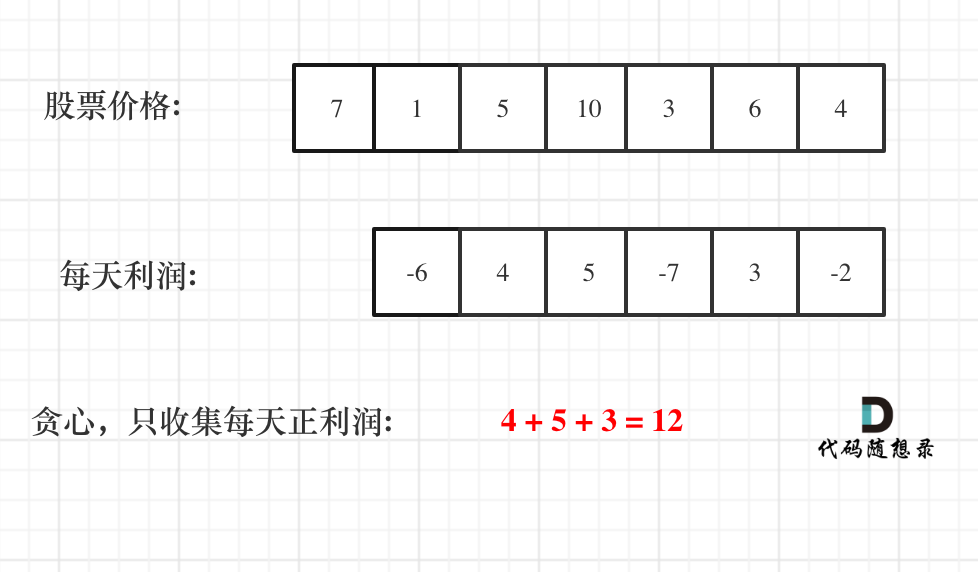
思路:最终利润是可以分解的!
把利润分解为每天为单位的维度，例如：假如第 0 天买入，第 3 天卖出，
那么利润为：prices[3] - prices[0]。相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

点击查看代码

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        result=0
        for i in range(1,len(prices)):
            sub=prices[i]-prices[i-1]
            if sub>0:
                result+=sub 
        return result

55. 跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。

解题：

思路：不一定非要明确一次究竟跳几步，每次取最大的跳跃步数，这个就是可以跳跃的覆盖范围。
这个范围内，别管是怎么跳的，反正一定可以跳过来。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！

写的第一个版本，就看i对应的最大范围，然后下一次i直接跳到cover。不能这样，会漏掉中间有可能扩大范围的值。还是得遍历。

点击查看代码

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        cover=0
        if len(nums)==1:
            return True
        i=0
        while i<=cover:
            cover=max(i+nums[i],cover)
            if cover>=len(nums)-1:
                return True
            i+=1
        return False  

1005.K次取反后最大化的数组和

给定一个整数数组 A，我们只能用以下方法修改该数组：我们选择某个索引 i 并将 A[i] 替换为 -A[i]，然后总共重复这个过程 K 次。（我们可以多次选择同一个索引 i。）
以这种方式修改数组后，返回数组可能的最大和。

解题：

思路：
（1）贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。
那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。
（2）又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值和可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。
步骤：
1.按照绝对值降序排序数组A
2.对负数/非正数执行取反操作
3.如果K的剩余次数为奇数，将绝对值最小的元素取反
4.计算数组A的元素和

点击查看代码

class Solution:
    def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:
        nums.sort(key=lambda x: abs(x),reverse=True)
        for i in range(len(nums)):
            if nums[i]<=0 and k>0:
                nums[i]*=-1
                k-=1
        if k%2==1:
            nums[-1]*=-1
        return sum(nums)   

python语法：
按绝对值（key）降序排序数组A：A.sort(key=lambda x:abs(x),reverse=True)
一种简洁的匿名函数定义方式,通常用于需要小型、一次性函数的场合：lambda 参数: 表达式