HDU - 6333 Problem B. Harvest of Apples

Problem B. Harvest of Apples

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 3752    Accepted Submission(s): 1442

Problem Description

There are n apples on a tree, numbered from 1 to n.
Count the number of ways to pick at most m apples.

 

 

Input

The first line of the input contains an integer T (1≤T≤105) denoting the number of test cases.
Each test case consists of one line with two integers n,m (1≤m≤n≤105).

 

 

Output

For each test case, print an integer representing the number of ways modulo 109+7.

 

 

Sample Input

2 5 2 1000 500

 

 

Sample Output

16 924129523

 

 

Source

2018 Multi-University Training Contest 4

 

 

Recommend

chendu   |   We have carefully selected several similar problems for you:  6447 6446 6445 6444 6443 

题意:给出n,m n个苹果最多取m个 求方案数

 

题解：

贴个官方题解，需要用到哦Lucas计算组合数

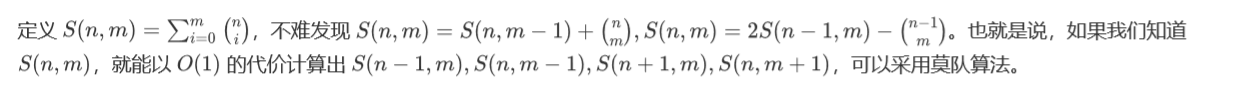
#include<bits/stdc++.h>
#define ll long long
#define mod 1000000007
using namespace std;
const int maxn = 100000+5;
int unit;
ll ans,res[maxn],inv[maxn],fac[maxn],inv_fac[maxn];
struct node
{
    ll l,r,id;
    bool friend operator < (const node u,const node v)
    {
        if(u.l/unit==v.l/unit)
            return u.r<v.r;
        else return u.l<v.l;
    }
} p[maxn];
void init()
{
    inv[0]=inv[1]=inv_fac[0]=fac[0]=1;
    for(int i=2; i<maxn; i++) inv[i]=inv[mod%i]*(mod-mod/i)%mod;
    for(int i=1; i<maxn; i++) fac[i]=fac[i-1]*i%mod;
    for(int i=1; i<maxn; i++) inv_fac[i]=inv_fac[i-1]*inv[i]%mod;
}
ll C(ll n,ll m)
{
    return fac[n]*inv_fac[m]%mod*inv_fac[n-m]%mod;
}
int main()
{
    int n,t;
    init();
    scanf("%d",&t);
    unit = sqrt(t)+0.5;
    for(int i=1; i<=t; i++)
    {
        scanf("%lld %lld",&p[i].r,&p[i].l);
        p[i].id=i*1ll;
    }
    sort(p+1,p+1+t);
    ll l=0,r=1;
    ans=1;
    for(int i=1; i<=t; i++)
    {
        while(r<p[i].r)
        {
            ans=(ans*2-C(r,l)+mod)%mod;
            r++;
        }
        while(r>p[i].r)
        {
            ans=1;
            l=0;
            r=p[i].r;
        }
        while(l<p[i].l)
        {
            ans=(ans+C(r,l+1)+mod)%mod;
            l++;
        }
        while(l>p[i].l)
        {
            ans=(ans-C(r,l)+mod)%mod;
            l--;
        }
        res[p[i].id]=ans;

    }
    for(int i=1; i<=t; i++)
        printf("%lld\n",res[i]);
}

 

 

PS:摸鱼怪的博客分享，欢迎感谢各路大牛的指点~