[SOJ #686]抢救(2019-11-7考试)/[洛谷P3625][APIO2009]采油区域
题目大意
有一个\(n\times m\)的网格,\((x,y)\)权值为\(a_{x,y}\),要求从中选取三个不相交的\(k\times k\)的正方形使得它们权值最大。\(n,m,k\leqslant1500\)
题解
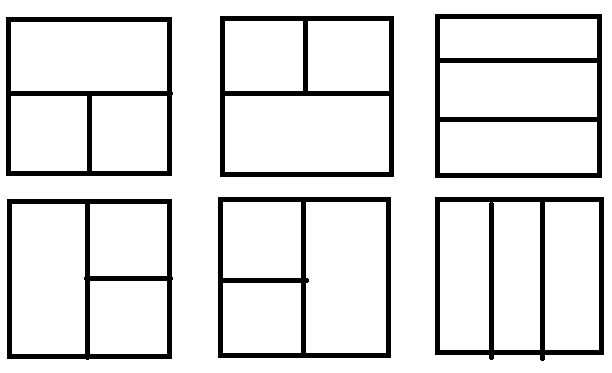
其实,只有如下六种方法分割网格:
对于每一种情况,我们在每个小方格中找最大的\(k\times k\)的正方形相加即可。可以令\(a[i][j],b[i][j],c[i][j],d[i][j]\)分别表示\((i,j)\)的左上、右上、左下、右下的区域中最大的\(k\times k\)的正方形的权值,然后就可以计算了
卡点
无
C++ Code:
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cctype>
const int maxn = 1510;
namespace io {
struct istream {
#define M (1 << 24)
char buf[M], *ch = buf - 1;
inline istream() { fread(buf, 1, M, stdin); }
inline istream& operator >> (int &x) {
while (isspace(*++ch));
for (x = *ch & 15; isdigit(*++ch); ) x = x * 10 + (*ch & 15);
return *this;
}
#undef M
} cin;
}
int n, m, k, ans, s[maxn][maxn];
int a[maxn][maxn], b[maxn][maxn], c[maxn][maxn], d[maxn][maxn];
/*
* a | b
* - - -
* c | d
*/
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
io::cin >> n >> m >> k;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
io::cin >> s[i][j];
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
s[i][j] += s[i][j - 1];
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
s[i][j] += s[i - 1][j];
for (int i = n; i >= k; --i)
for (int j = m; j >= k; --j)
s[i][j] += s[i - k][j - k] - s[i - k][j] - s[i][j - k];
for (int i = k; i <= n; ++i)
for (int j = k; j <= m; ++j)
a[i][j] = std::max({ s[i][j], a[i - 1][j], a[i][j - 1] });
for (int i = k; i <= n; ++i)
for (int j = m - k + 1; j; --j)
b[i][j] = std::max({ s[i][j + k - 1], b[i - 1][j], b[i][j + 1] });
for (int i = n - k + 1; i; --i)
for (int j = k; j <= m; ++j)
c[i][j] = std::max({ s[i + k - 1][j], c[i + 1][j], c[i][j - 1] });
for (int i = n - k + 1; i; --i)
for (int j = m - k + 1; j; --j)
d[i][j] = std::max({ s[i + k - 1][j + k - 1], d[i + 1][j], d[i][j + 1] });
for (int i = k; i <= n - k; ++i)
for (int j = k; j <= m - k; ++j)
ans = std::max(ans, a[i][j] + b[i][j + 1] + c[i + 1][m]);
for (int i = k; i <= n - k; ++i)
for (int j = k; j <= m - k; ++j)
ans = std::max(ans, a[i][m] + c[i + 1][j] + d[i + 1][j + 1]);
for (int i = k; i <= n - k; ++i)
for (int j = k; j <= m - k; ++j)
ans = std::max(ans, a[i][j] + c[i + 1][j] + b[n][j + 1]);
for (int i = k; i <= n - k; ++i)
for (int j = k; j <= m - k; ++j)
ans = std::max(ans, a[n][j] + b[i][j + 1] + d[i + 1][j + 1]);
for (int i = k; i <= n; ++i)
for (int j = 2 * k; j <= m - k; ++j)
ans = std::max(ans, s[i][j] + a[n][j - k] + b[n][j + 1]);
for (int i = 2 * k; i <= n - k; ++i)
for (int j = k; j <= m; ++j)
ans = std::max(ans, s[i][j] + a[i - k][m] + c[i + 1][m]);
std::cout << ans << '\n';
return 0;
}