[Atcoder AGC032C]Three Circuits

题目大意：有一张$n$个点$m$条边的无向连通图，判断是否可以从中分出$3$个环，满足三个环覆盖整张图并且没有重复的边。$n,m\leqslant10^5$

题解：分类讨论。有度数为奇肯定不行，因为连通，所以若环数目大于$3$一定可以合并，所以只需要排除环数目小于$3$的情况。

当所有点度数小于$4$时肯定不行，当最大的度数大于$4$时一定可以。接下来就讨论最大点度数为$4$的情况。当只有一个点度数为$4$时，相当于两个自环，不可以。当有大于两个点度数为$4$时可以。有两个点度数为$4$时，除了下面这种情况其余均可。

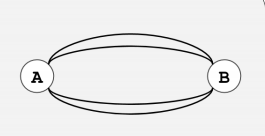
而这种情况的判断只需要看点$A$是否可以不通过点$B$回到自身，是就可以，否则就是上面这种情况。

卡点：无

 

C++ Code：

#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
const int maxn = 1e5 + 10;

int n, m, deg[maxn], Max, Cnt, A, B;

int head[maxn], cnt;
struct Edge { int to, nxt; } e[maxn << 1];
void addedge(int a, int b) {
	e[++cnt] = (Edge) { b, head[a] }; head[a] = cnt;
	e[++cnt] = (Edge) { a, head[b] }; head[b] = cnt;
	++deg[a], ++deg[b];
}

void dfs(int u, int fa = 0) {
	if (u == A && fa) std::cout << "Yes\n", exit(0);
	if (u == B) return ;
	for (int i = head[u], v; i; i = e[i].nxt)
		if ((v = e[i].to) != fa) dfs(v, u);
}
int main() {
	std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
	std::cin >> n >> m;
	for (int i = 0, a, b; i < m; ++i) std::cin >> a >> b, addedge(a, b);
	for (int i = 1; i <= n; ++i) if (deg[i] & 1) {
		std::cout << "No\n";
		return 0;
	} else {
		Max = std::max(Max, deg[i]);
		if (deg[i] == 4) { ++Cnt; if (A) B = i; else A = i; }
	}
	if (Max < 4 || (Max == 4 && Cnt == 1)) { std::cout << "No\n"; return 0; }
	if (Max > 4 || Cnt > 2) { std::cout << "Yes\n"; return 0; }
	dfs(A), std::cout << "No\n";
	return 0;
}