T1：Attack
答案为 \(\lceil\frac{A}{B}\rceil\)
代码实现
a, b = map(int, input().split())
print((a+b-1)//b)
T2：Find snuke
爆搜
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
int di[] = {-1, -1, -1, 0, 0, 1, 1, 1};
int dj[] = {-1, 0, 1, -1, 1, -1, 0, 1};
int main() {
int h, w;
cin >> h >> w;
vector<string> s(h);
rep(i, h) cin >> s[i];
string T = "snuke";
rep(si, h)rep(sj, w) {
rep(v, 8) {
int i = si, j = sj;
rep(k, 5) {
if (i < 0 or j < 0 or i >= h or j >= w) break;
if (s[i][j] != T[k]) break;
if (k == 4) {
i = si; j = sj;
rep(nk, 5) {
cout << i+1 << ' ' << j+1 << '\n';
i += di[v]; j += dj[v];
}
return 0;
}
i += di[v]; j += dj[v];
}
}
}
return 0;
}
T3：Almost Equal
爆搜
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<string> s(n);
rep(i, n) cin >> s[i];
sort(s.begin(), s.end());
do {
bool ok = true;
rep(i, n-1) {
int d = 0;
rep(j, m) if (s[i][j] != s[i+1][j]) d++;
if (d != 1) ok = false;
}
if (ok) {
puts("Yes");
return 0;
}
} while (next_permutation(s.begin(), s.end()));
puts("No");
return 0;
}
T4：Impartial Gift
双指针或者二分
枚举给青木的礼物 \(x\)，给snuke的礼物就选价值范围为 \([x-d, x+d]\) 中价值最大的礼物
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
using ll = long long;
int main() {
int n, m; ll d;
cin >> n >> m >> d;
vector<ll> a(n), b(m);
rep(i, n) cin >> a[i];
rep(i, m) cin >> b[i];
sort(a.begin(), a.end());
sort(b.begin(), b.end());
ll ans = -1;
rep(i, n) {
ll l = a[i]-d, r = a[i]+d;
int j = upper_bound(b.begin(), b.end(), r)-b.begin();
if (j > 0) {
ll x = b[j-1];
if (l <= x) {
ans = max(ans, a[i]+x);
}
}
}
cout << ans << '\n';
return 0;
}
T5：Isolation
可以用 std::unordered_set 来维护邻接表
一开始的答案为 \(n\)，然后考虑每次的操作对答案的影响即可
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
using ll = long long;
int main() {
int n, q;
cin >> n >> q;
vector<unordered_set<int>> to(n);
int ans = n;
rep(qi, q) {
int type;
cin >> type;
if (type == 1) {
int a, b;
cin >> a >> b;
--a; --b;
if (to[a].size() == 0) ans--;
if (to[b].size() == 0) ans--;
to[a].insert(b);
to[b].insert(a);
}
else {
int v;
cin >> v;
--v;
if (to[v].size()) {
for (int u : to[v]) {
to[u].erase(v);
if (to[u].size() == 0) ans++;
}
to[v].clear();
ans++;
}
}
cout << ans << '\n';
}
return 0;
}
T6：Merge Set
对任意两个有公共元素的集合进行连边，进行一次操作就相当于经过一条边，那么在这个图上从 \(1\) 走到 \(M\) 的最短路就是答案。
但这样显然会超时
优化方法：可以将每个集合 \(S_i\) 视为中转点，将 \(S_i\) 里每个数都和这个中转点进行连边，这样一来对每个集合作图的时间就是 \(O(A_i)\)
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> to(n+m);
rep(i, n) {
int a;
cin >> a;
rep(j, a) {
int x;
cin >> x;
--x;
to[x].push_back(m+i);
to[m+i].push_back(x);
}
}
const int INF = 1001001001;
vector<int> dist(n+m, INF);
queue<int> q;
dist[0] = 0; q.push(0);
while (q.size()) {
int v = q.front(); q.pop();
for (int u : to[v]) {
if (dist[u] != INF) continue;
dist[u] = dist[v]+1;
q.push(u);
}
}
int ans = dist[m-1];
if (ans == INF) ans = -1;
else ans = (ans-2)/2;
cout << ans << '\n';
return 0;
}
T7：Sort from 1 to 4
假设将 \(A\) 做升序排序后的序列是 \(B\)，考虑从 \(A_i\) 到 \(B_i\) 连一条边，那么我们可以得到一个 \(4\) 个点 \(N\) 条边的有向图。
结论：答案为 \(N -\) 图上的环数
为了使得答案最大，我们应该尽可能地使环数变多。首先，自环和 \(2\) 元环是固定不变的，\(3\) 元环和 \(4\) 元环可以放在一起考虑
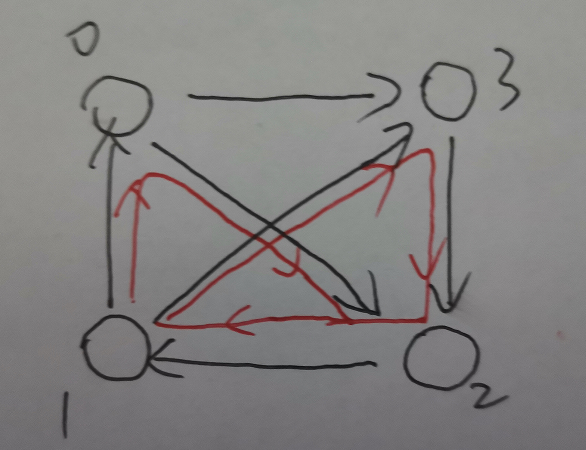
在上图中，\(4\) 元环中可能包含 \(2\) 种 \(3\) 元环，通过改变这 \(4\) 个点的位置可以使其中包含的 \(3\) 元环的个数尽可能的多
假设 \(x_3\) 为 \(3\) 元环的个数，\(x_4\) 为 \(4\) 元环的个数，\(es\) 为 \(3\) 元环和 \(4\) 元环的总边数，那么 \(es=3x_3+4x_4\)
我们一旦求出了 \(x_3\)，就能通过 \(x_4 = \frac{es-3x_3}{4}\) 求出 \(x_4\)
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a(n);
rep(i, n) cin >> a[i];
rep(i, n) a[i]--;
auto b = a;
sort(b.begin(), b.end());
int m = 4;
vector g(m, vector<int>(m));
rep(i, n) g[a[i]][b[i]]++;
int ans = 0;
rep(i, m) {
ans += g[i][i];
g[i][i] = 0;
}
rep(i, m)rep(j, i) {
int c = min(g[i][j], g[j][i]);
ans += c;
g[i][j] -= c;
g[j][i] -= c;
}
{
int es = 0;
rep(i, m)rep(j, m) es += g[i][j];
vector<int> p(m);
iota(p.begin(), p.end(), 0);
int x3 = 0;
do {
int now = 0;
int a = g[p[2]][p[1]];
int b = min(g[p[1]][p[0]], g[p[0]][p[2]]);
int c = min(g[p[1]][p[3]], g[p[3]][p[2]]);
now = min(a, b+c);
x3 = max(x3, now);
} while (next_permutation(p.begin(), p.end()));
int x4 = (es-x3*3)/4;
ans += x3+x4;
}
cout << n-ans << '\n';
return 0;
}
