YACS2022年9月甲组

T1：游戏体验

固定区间左端点，一边枚举区间右端点，一边计算把右端点加入当前区间后得到的区间总分数，时间复杂度为 $O(m^2)$。一个区间新加入一个数 $x$ 要分 $3$ 种情况：$x$ 出现一次，区间总分数加上 $x$ 对应的分数；$x$ 出现两次，区间总分数减去 $x$ 对应的分数；$x$ 出现三次及三次以上就不需要再考虑了。

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
 
using namespace std;
using ll = long long;
 
inline void chmax(ll& x, ll y) { if (x < y) x = y; }
 
int main() {
    int n;
    cin >> n;
    vector<int> a(n);
    rep(i, n) cin >> a[i];
    
    int m;
    cin >> m;
    vector<int> x(m);
    rep(i, m) cin >> x[i], x[i]--;
    
    ll ans = 0;
    rep(l, m) {
        ll now = 0;
        vector<int> cnt(n);
        for (int r = l; r < m; ++r) {
            int i = x[r];
            cnt[i]++;
            if (cnt[i] == 1) now += a[i];
            else if (cnt[i] == 2) now -= a[i];
            chmax(ans, now);
        }
    }
    
    cout << ans << '\n';
    
    return 0;
}

记 f[i] 表示以 $i$ 为左端点在当前时刻的区间的得分
记 pre[i] 表示和位置 $i$ 相同的数，上一个位置是什么？

当加入新的数 $x$ 时，从上一个和 $x$ 相同的之后一个位置到当前位置的所有 f[i] 都增加 $a_x$ 分；从当前位置往左数第 $2$ 个和 $x$ 相同的位置的之后一个位置到上一个和 $x$ 相同的位置之间的所有 f[i] 都减少 $a_x$ 分；从上一个和 $x$ 相同的位置开始的左边的所有 f[i] 都加上 $a_x$ 分

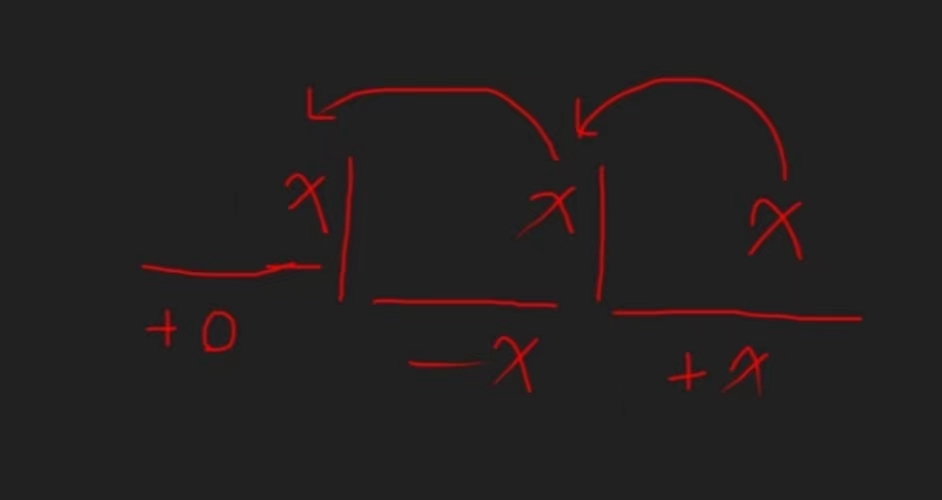
有区间查询和区间更新，所以可以用线段树来维护。但这里 $m$ 是 $1e6$，会比较卡线段树，所以需要用zkw线段树。

T2：区间交集（三）

70 分做法：

见 link