T1:Cow College
总学费 设置的单人学费 接受的奶牛数
一旦固定单人学费,就能确定接受的奶牛数
单人学费可以是哪些值?
其中之一作为学费门槛
暴力做法是先枚举单人学费是多少,再查看每个人的可接受学费是否大于等于单人学费,复杂度为
可以通过对序列 做降序排序来优化掉第二重循环
代码实现
n = int(input()) c = list(map(int, input().split())) c.sort(reverse=True) tot, ans = 0, 0 for i in range(n): if (i+1)*c[i] >= tot: tot = (i+1)*c[i] ans = c[i] print(tot, ans)
T2:Feeding the Cows B
对每头 G,尽可能往右放 G 草地
对每头 H,允许(若越界)回过头往左找空地
可能带来的问题:
- 找不到
- 时间复杂度
- 整体最优解
-
找不到---无解
,原地待命
,种草稀疏
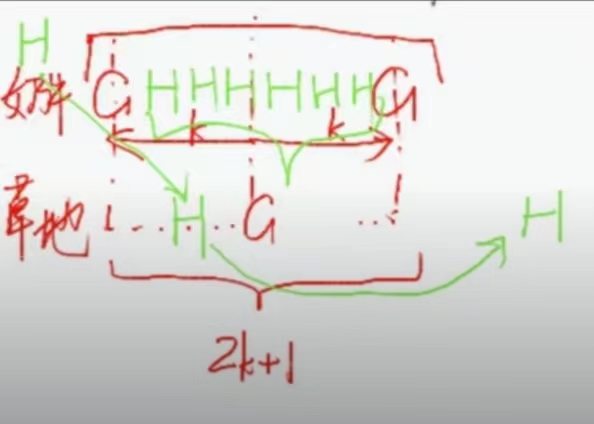
-
时间复杂度
从左回头找最多只会出现一次 -
最优解
关键:G/H 草地不会互相抢占位置
代码实现
#include <bits/stdc++.h> #define rep(i, n) for (int i = 0; i < (n); ++i) using namespace std; void solve() { int n, k; cin >> n >> k; string s; cin >> s; int cnt = 0; string ans = string(n, '.'); // G rep(i, n) { if (s[i] == 'H') continue; int pos = min(i+k, n-1); ans[pos] = 'G'; ++cnt; i = pos+k; } // H rep(i, n) { if (s[i] == 'G') continue; int pos = min(i+k, n-1); while (ans[pos] != '.') --pos; ans[pos] = 'H'; ++cnt; i = pos+k; } cout << cnt << '\n' << ans << '\n'; } int main() { int t; cin >> t; while (t--) solve(); return 0; }
T3:Reverse Engineering
程序分为有条件返回和无条件返回
有条件返回形如
if (b[i] == x) return y;
标准化(normalize),对于可能性很多的复杂性事物,我们可以人为地制定一些规则使其有统一格式
- 每一变量只判断一次
- 程序一定可以写成 行
算法:
- 寻找一列 ,枚举 ,判断能否有
if (b[i] == x) return y; - 如果找到,则筛去 的行,并筛去列
如果找不到,判断:若所有输入都返回,则输出OK,否则矛盾,输出LTE - 回到步骤 ,总共 次
- 最后判断能否无条件返回
总时间复杂度为:
代码实现
#include <bits/stdc++.h> #define rep(i, n) for (int i = 0; i < (n); ++i) using namespace std; bool vr[105], vc[105]; void solve() { memset(vr, false, sizeof vr); memset(vc, false, sizeof vc); int n, m; cin >> n >> m; vector<string> s(m); vector<int> val(m); rep(i, m) cin >> s[i] >> val[i]; auto Return = [&](int id, int x, int y) { rep(i, m) { if (vr[i]) continue; if (s[i][id]-'0' == x) { if (val[i] != y) return false; } } return true; }; auto Return2 = [&](int y) { rep(i, m) { if (vr[i]) continue; if (val[i] != y) return false; } return true; }; auto ok = [&]{ rep(i, n) { bool found = false; // 判断是否有 if (b[j] == x) return y; 这一程序语句是否成立 -> Return(j, x, y) rep(j, n) if (!found) { rep(x, 2) if (!found) { rep(y, 2) if (!found) { if (!vc[j] and Return(j, x, y)) { found = vc[j] = true; rep(k, m) { // 这一输入不能因为之前的程序语句就结束了,因此这一行要未被筛选过 if (!vr[k] and s[k][j]-'0' == x) { vr[k] = true; } } } } } } if (!found) break; } return Return2(0) or Return2(1); }(); if (ok) puts("OK"); else puts("LIE"); } int main() { int t; cin >> t; while (t--) solve(); return 0; }




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现