T1:矩形覆盖
用 std::set 或线段树来维护扫描线即可
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)
using std::cin;
using std::cout;
using std::multiset;
using ll = long long;
struct Node {
ll x, h;
int type;
bool operator<(const Node &o) const {
return x < o.x;
}
} a[600005];
int main() {
int n;
cin >> n;
rep(i, n) {
int s, t, h;
cin >> s >> t >> h;
a[i*2-1] = {s, h, 0}; // 0 表示左边界
a[i*2] = {t, h, 1}; // 1 表示右边界
}
int n2 = n*2;
std::sort(a+1, a+n2+1);
ll ans = 0;
ll last = 0; // 扫描线上一次扫过的矩形高度的位置
multiset<ll> st; // 维护当前存活着的的矩形高度
st.insert(0);
for (int i = 1; i <= n2;) {
ll x = a[i].x;
ans += *st.rbegin()*(a[i].x-last);
last = a[i].x;
while (i <= n2 and a[i].x == last) {
if (a[i].type) st.erase(st.find(a[i].h));
else st.insert(a[i].h);
++i;
}
}
cout << ans << '\n';
return 0;
}
T2: 评测队列(二)
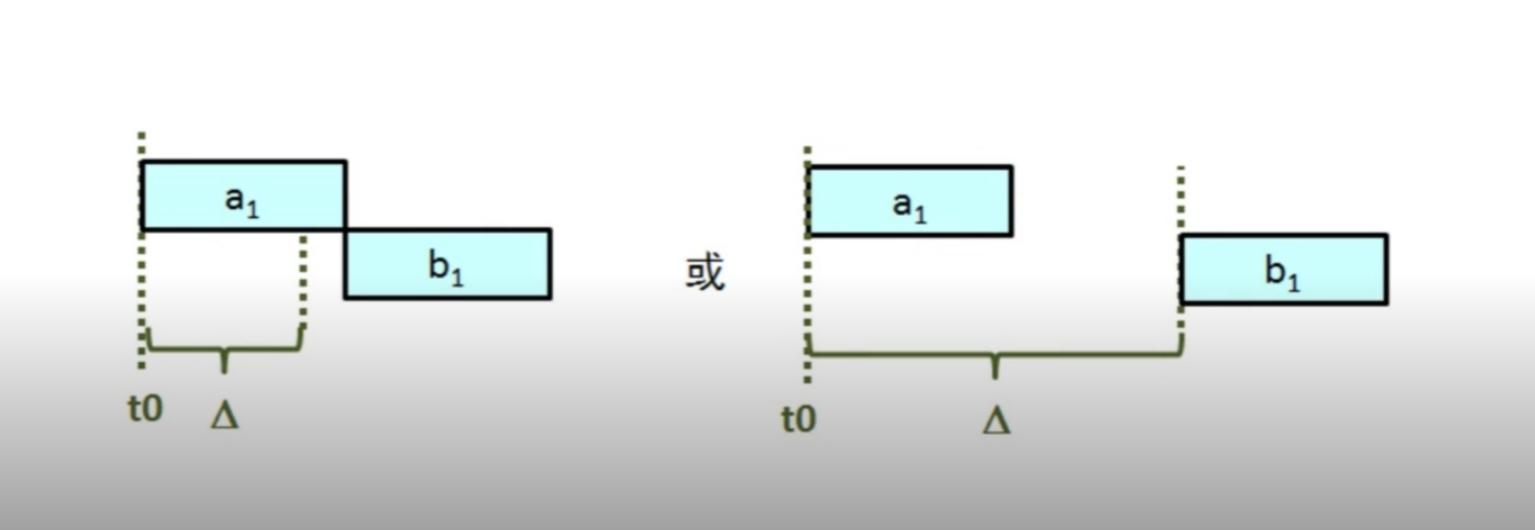
假设 \(t_0 + △\) 后 \(M_2\) 才空闲,运行开始的时间是 \(\max(△, a_1)\)
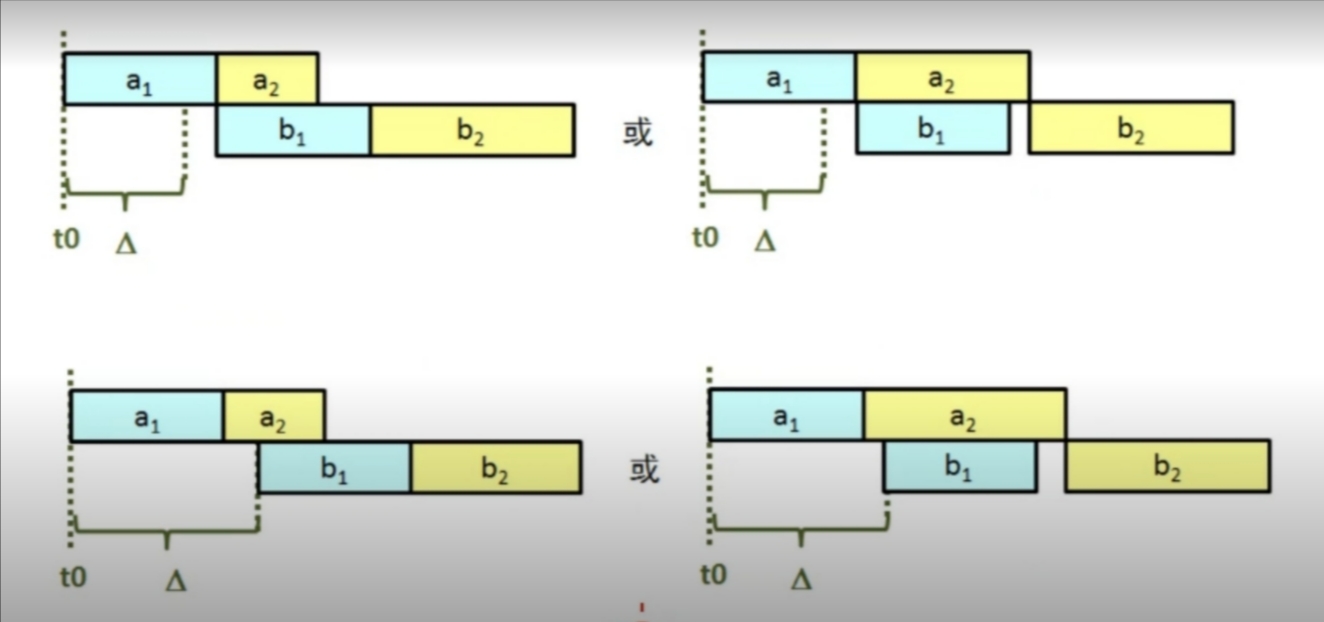
交换前:\(t_0 + \max\{a_1+b_1, a_1+a_2, △+b_1\} + b_2\)
交换后:\(t_0 + \max\{a_2+b_2, a_2+a_1, △+b_2\} + b_1\)
情况1:\(a_2 = \min\{a_1, a_2, b_1, b_2\}\)
交换前: \(t_0 + \max\{a_1+b_1, a_1+a_2, △+b_1\} + b_2 = t_0 + \max\{a_1+b_1, △+b_1\} + b_2 = t_0 + \max\{a_1, △\} + b_1+b_2 = t_0 + \max\{a_1+b_2, △+b_2\} + b_1\)
交换后:\(t_0 + \max\{a_2+b_2, a_2+a_1, △+b_2\} + b_1\)
可推出上式 \(\geqslant\) 下式,这样交换一定是不亏的
情况2:\(b_1 = \min\{a_1, a_2, b_1, b_2\}\)
交换前:\(t_0 + \max\{a_1+b_1, a_1+a_2, △+b_1\} + b_2 = t_0 + \max\{a_1+a_2, △+b_1\} + b_2 = t_0 + \max\{a_1+a_2+b_2, △+b_1+b_2\}\)
交换后:\(t_0 + \max\{a_2+b_2, a_2+a_1, △+b_2\} + b_1 = t_0 + \max\{a_2+b_2+b_1, a_2+a_1+b_1, △+b_2+b_1\}\)
可推出上式 \(\geqslant\) 下式,这样交换一定是不亏的
结论:
如果满足
\(\hspace{3cm} b_1 = \min\{a_1, a_2, b_1, b_2\} \) 或 \(a_2 = \min\{a_1, a_2, b_1, b_2\}\)
则交换
也就是说我们应当使结果满足
也叫 \(\operatorname{Johnson}\) 不等式
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::min;
using std::max;
struct Node {
int a, b;
bool operator<(const Node &o) const {
return min(o.b, a) < min(b, o.a);
}
} p[200005];
int main() {
int n;
cin >> n;
rep(i, n) cin >> p[i].a >> p[i].b;
std::sort(p, p+n);
int s1 = 0, s2 = 0;
rep(i, n) {
s1 += p[i].a;
s2 = max(s1, s2) + p[i].b;
}
cout << s2 << '\n';
return 0;
}
T3: 殊途同归
注意虽然不允许两条路径有重边,但允许有重复的点
其实本题是一道费用流的模板题
本题的建图比较简单:只需开源点 \(S\) 和汇点 \(T\),从点 \(S\) 到 \(1\) 连一条有向边,这条边的容量是 \(2\)、费用是 \(0\),类似地,从点 \(N\) 到 \(T\) 连一条有向边,这条边的容量是 \(2\)、费用是 \(0\)
(可行流是 \(2\),是因为题目让我们找到两条路径;费用是 \(0\),是因为这两个点是虚拟的点,不产生费用)
对于其他边,容量都是 \(1\),费用是相应边权
代码实现
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)
using std::cin;
using std::cout;
using std::vector;
using ll = long long;
namespace internal {
template <class E> struct csr {
std::vector<int> start;
std::vector<E> elist;
explicit csr(int n, const std::vector<std::pair<int, E>>& edges)
: start(n + 1), elist(edges.size()) {
for (auto e : edges) {
start[e.first + 1]++;
}
for (int i = 1; i <= n; i++) {
start[i] += start[i - 1];
}
auto counter = start;
for (auto e : edges) {
elist[counter[e.first]++] = e.second;
}
}
};
} // namespace internal
template<class Cap, class Cost>
struct mcf_graph {
public:
mcf_graph() {}
explicit mcf_graph(int n) : _n(n) {}
int add_edge(int from, int to, Cap cap, Cost cost) {
assert(0 <= from && from < _n);
assert(0 <= to && to < _n);
assert(0 <= cap);
assert(0 <= cost);
int m = int(_edges.size());
_edges.push_back({from, to, cap, 0, cost});
return m;
}
struct edge {
int from, to;
Cap cap, flow;
Cost cost;
};
edge get_edge(int i) {
int m = int(_edges.size());
assert(0 <= i && i < m);
return _edges[i];
}
std::vector<edge> edges() { return _edges; }
std::pair<Cap, Cost> flow(int s, int t) {
return flow(s, t, std::numeric_limits<Cap>::max());
}
std::pair<Cap, Cost> flow(int s, int t, Cap flow_limit) {
return slope(s, t, flow_limit).back();
}
std::vector<std::pair<Cap, Cost>> slope(int s, int t) {
return slope(s, t, std::numeric_limits<Cap>::max());
}
std::vector<std::pair<Cap, Cost>> slope(int s, int t, Cap flow_limit) {
assert(0 <= s && s < _n);
assert(0 <= t && t < _n);
assert(s != t);
int m = int(_edges.size());
std::vector<int> edge_idx(m);
auto g = [&]() {
std::vector<int> degree(_n), redge_idx(m);
std::vector<std::pair<int, _edge>> elist;
elist.reserve(2 * m);
for (int i = 0; i < m; i++) {
auto e = _edges[i];
edge_idx[i] = degree[e.from]++;
redge_idx[i] = degree[e.to]++;
elist.push_back({e.from, {e.to, -1, e.cap - e.flow, e.cost}});
elist.push_back({e.to, {e.from, -1, e.flow, -e.cost}});
}
auto _g = internal::csr<_edge>(_n, elist);
for (int i = 0; i < m; i++) {
auto e = _edges[i];
edge_idx[i] += _g.start[e.from];
redge_idx[i] += _g.start[e.to];
_g.elist[edge_idx[i]].rev = redge_idx[i];
_g.elist[redge_idx[i]].rev = edge_idx[i];
}
return _g;
}();
auto result = slope(g, s, t, flow_limit);
for (int i = 0; i < m; i++) {
auto e = g.elist[edge_idx[i]];
_edges[i].flow = _edges[i].cap - e.cap;
}
return result;
}
private:
int _n;
std::vector<edge> _edges;
// inside edge
struct _edge {
int to, rev;
Cap cap;
Cost cost;
};
std::vector<std::pair<Cap, Cost>> slope(internal::csr<_edge>& g,
int s,
int t,
Cap flow_limit) {
// variants (C = maxcost):
// -(n-1)C <= dual[s] <= dual[i] <= dual[t] = 0
// reduced cost (= e.cost + dual[e.from] - dual[e.to]) >= 0 for all edge
// dual_dist[i] = (dual[i], dist[i])
std::vector<std::pair<Cost, Cost>> dual_dist(_n);
std::vector<int> prev_e(_n);
std::vector<bool> vis(_n);
struct Q {
Cost key;
int to;
bool operator<(Q r) const { return key > r.key; }
};
std::vector<int> que_min;
std::vector<Q> que;
auto dual_ref = [&]() {
for (int i = 0; i < _n; i++) {
dual_dist[i].second = std::numeric_limits<Cost>::max();
}
std::fill(vis.begin(), vis.end(), false);
que_min.clear();
que.clear();
// que[0..heap_r) was heapified
size_t heap_r = 0;
dual_dist[s].second = 0;
que_min.push_back(s);
while (!que_min.empty() || !que.empty()) {
int v;
if (!que_min.empty()) {
v = que_min.back();
que_min.pop_back();
} else {
while (heap_r < que.size()) {
heap_r++;
std::push_heap(que.begin(), que.begin() + heap_r);
}
v = que.front().to;
std::pop_heap(que.begin(), que.end());
que.pop_back();
heap_r--;
}
if (vis[v]) continue;
vis[v] = true;
if (v == t) break;
// dist[v] = shortest(s, v) + dual[s] - dual[v]
// dist[v] >= 0 (all reduced cost are positive)
// dist[v] <= (n-1)C
Cost dual_v = dual_dist[v].first, dist_v = dual_dist[v].second;
for (int i = g.start[v]; i < g.start[v + 1]; i++) {
auto e = g.elist[i];
if (!e.cap) continue;
// |-dual[e.to] + dual[v]| <= (n-1)C
// cost <= C - -(n-1)C + 0 = nC
Cost cost = e.cost - dual_dist[e.to].first + dual_v;
if (dual_dist[e.to].second - dist_v > cost) {
Cost dist_to = dist_v + cost;
dual_dist[e.to].second = dist_to;
prev_e[e.to] = e.rev;
if (dist_to == dist_v) {
que_min.push_back(e.to);
} else {
que.push_back(Q{dist_to, e.to});
}
}
}
}
if (!vis[t]) {
return false;
}
for (int v = 0; v < _n; v++) {
if (!vis[v]) continue;
// dual[v] = dual[v] - dist[t] + dist[v]
// = dual[v] - (shortest(s, t) + dual[s] - dual[t]) +
// (shortest(s, v) + dual[s] - dual[v]) = - shortest(s,
// t) + dual[t] + shortest(s, v) = shortest(s, v) -
// shortest(s, t) >= 0 - (n-1)C
dual_dist[v].first -= dual_dist[t].second - dual_dist[v].second;
}
return true;
};
Cap flow = 0;
Cost cost = 0, prev_cost_per_flow = -1;
std::vector<std::pair<Cap, Cost>> result = {{Cap(0), Cost(0)}};
while (flow < flow_limit) {
if (!dual_ref()) break;
Cap c = flow_limit - flow;
for (int v = t; v != s; v = g.elist[prev_e[v]].to) {
c = std::min(c, g.elist[g.elist[prev_e[v]].rev].cap);
}
for (int v = t; v != s; v = g.elist[prev_e[v]].to) {
auto& e = g.elist[prev_e[v]];
e.cap += c;
g.elist[e.rev].cap -= c;
}
Cost d = -dual_dist[s].first;
flow += c;
cost += c * d;
if (prev_cost_per_flow == d) {
result.pop_back();
}
result.push_back({flow, cost});
prev_cost_per_flow = d;
}
return result;
}
};
int main() {
int n, m;
cin >> n >> m;
int sv = n+1, tv = n+2;
mcf_graph<int, ll> g(tv+1);
g.add_edge(sv, 1, 2, 0);
g.add_edge(n, tv, 2, 0);
rep(i, m) {
int u, v, w;
cin >> u >> v >> w;
g.add_edge(u, v, 1, w);
}
ll ans = g.flow(sv, tv).second;
cout << ans << '\n';
return 0;
}



