排序算法

一：排序的分类

排序主要分为内部排序和外部排序两大类：其中内部排序将所有的数据都加载到内存中；外部排序由于数据量过大，需要借助外部存储进行排序。主要学习内排序的八种排序算法。

 二：各排序算法的稳定性与时间复杂度

 

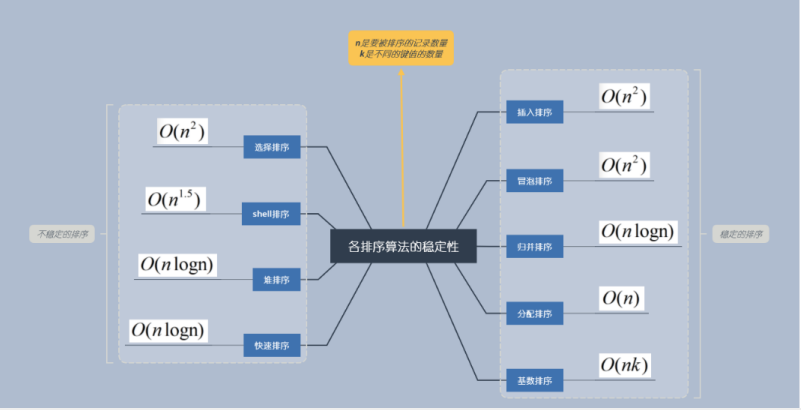
三：插入排序

（1）直接插入排序

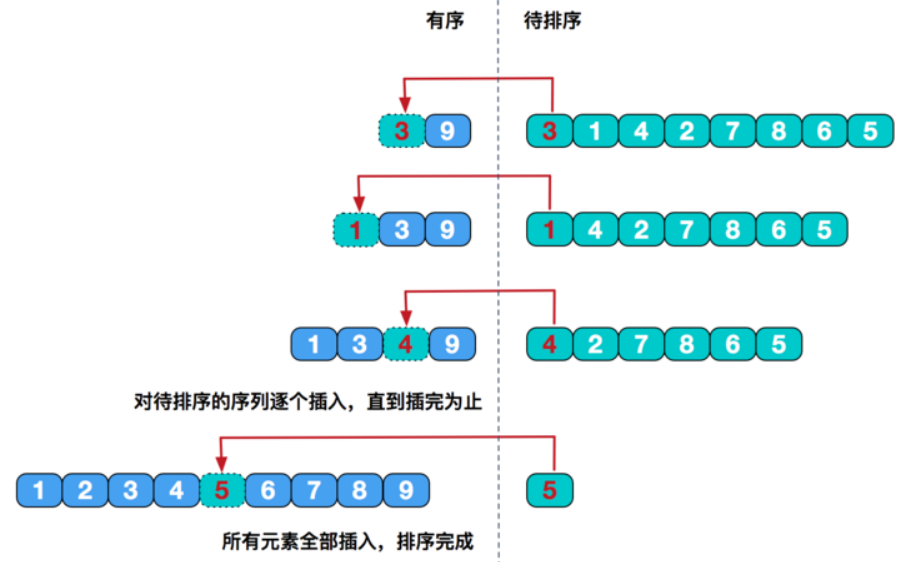
import java.lang.reflect.Array;
import java.util.Arrays;

public class Solution {
    public static void main(String[] args) {
        InsertSort(new int[] { 9 ,20 , 10, 13 , 12});
    }
    public static void InsertSort(int [] arr){
        int value;//待插入元素
        int index;//初始值为待插入元素前一个元素的索引

        for(int i= 1 ; i< arr.length;i++){
            //i从第二个元素开始，默认第一个元素是有序的
            //循环条件是小于数组长度，因为也要将最后一个元素插入到前面的序列
            value = arr[i];
            index = i - 1;//初始为前一个元素
            while(index >=0 && value < arr[index]){
                //需要保证index合法
                //每当前面的元素比待插入元素大，就向后移动
                arr[index + 1] = arr[index];
                //不用怕覆盖，因为value保存着待插入的值
                index--;
            }
            //当退出循环，表明已经找到了待插入位置，即index + 1
            arr[index + 1] = value;
        }

        System.out.println(Arrays.toString(arr));
    }
}

简单插入排序存在的问题：当需要插入的数是较小的数时，后移的次数明显增多，对效率有影响。

（2）希尔排序

希尔排序时简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。

基本思想：

/**
 * 希尔排序演示
 */
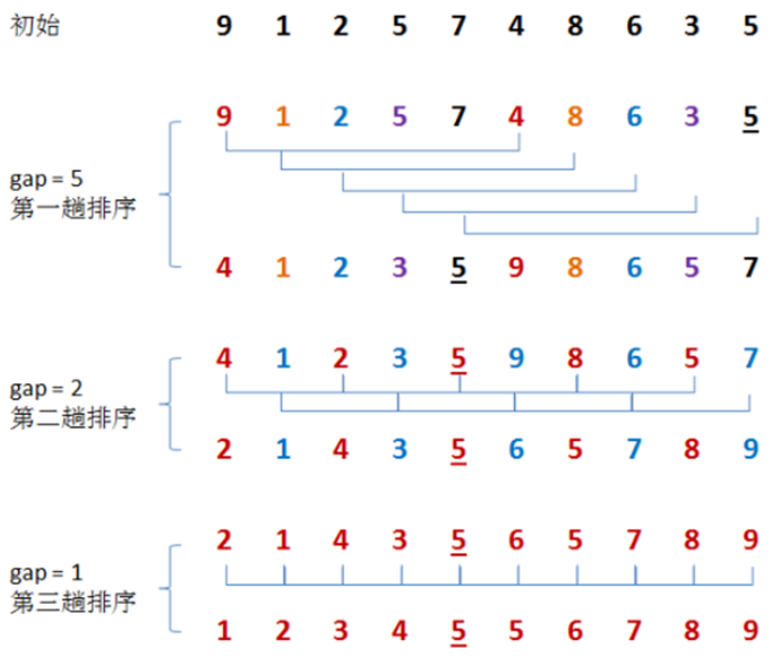
public class ShellSort {
    public static void main(String[] args) {
        int[] arr = {5, 1, 7, 3, 1, 6, 9, 4};
        shellSort(arr);

        for (int i : arr) {
            System.out.print(i + "\t");
        }
    }

    private static void shellSort(int[] arr) {
        //step:步长
        for (int step = arr.length / 2; step > 0; step /= 2) {
            //从第step个元素开始，逐个对当前元素所在的组进行插入排序。
            for (int i = step; i < arr.length; i++) {
                int value = arr[i];
                int j=i;
　　　　　　　　　　 //找插入位置，并将当前组中比当前元素大的值后移
　　　　　　　　　　 while(j-step>=0 && arr[j]<arr[j-step]){
　　　　　　　　　　　　　 arr[j]=arr[j-step];
　　　　　　　　　　 　　　j -= step;
　　　　　　　　　　 }
            　　　//找到插入位置
　　　　　　　　　　　arr[j] = value;
            }
        }
    }
}

四：选择排序：

（1）简单选择排序（每次选择最小的值放在组头，缩小组的范围）（ O(n2) ）

基本思想：给定数组：int[] arr={里面n个数据}；第1趟排序，在待排序数据arr[1]~arr[n]中选出最小的数据，将它与arrr[1]交换；第2趟，在待排序数据arr[2]~arr[n]中选出最小的数据，将它与r[2]交换；以此类推，第i趟在待排序数据arr[i]~arr[n]中选出最小的数据，将它与r[i]交换，直到全部排序完成。

（2）堆排序

基本思想：

1. 构建初始堆，将待排序列构成一个大顶堆(或者小顶堆)，升序大顶堆，降序小顶堆；（第一次构建堆时从下往上，从最后一个非叶子结点开始调整，一共有 （arr.length/2 - 1）个非叶子结点）
2. 将堆顶元素与堆尾元素交换，并断开(从待排序列中移除)堆尾元素。
3. 重新构建堆。注意，由于交换头尾元素后，其他结点仍满足大顶堆，故这时重新调整仅需要从根节点开始即可（不必再从最后一个非叶子结点开始）。
4. 重复2~3，直到待排序列中只剩下一个元素(堆顶元素)。

public class heapSort {
    public static void main(String[] args) {
        int[] nums = new int[]{5, 3, 10, 65, 4, 8, 19, 9, 2, 0};
        heapSort h = new heapSort();
        //先从头创建大顶堆
        h.MaxHeap(nums);
        //每次将堆顶最大值与堆尾交换，舍弃堆尾（即将堆长度减一），并重新调整新的堆
        for (int i = nums.length - 1; i >= 0; i--) {
            int temp = nums[0];
            nums[0]=nums[i];
            nums[i]=temp;
            h.adjustHeap(nums,0,i);
        }
        for (int num : nums) {
            System.out.println(num);
        }
//        h.MinHeap(nums);
//        for(int num:nums){
//            System.out.println(num);
//        }
    }

    //构建大顶堆
    public void MaxHeap(int[] arr){
        for(int i=arr.length/2 - 1; i>=0; i--){
            adjustHeap(arr,i,arr.length);
        }
    }

    //调整大顶堆,l,r是左右孩子，maxindex是当前要调整的结点
    public void  adjustHeap(int[] arr,int i,int length){
        int l = 2*i+1, r = 2*i+2, maxindex=i;
        if(l<length && arr[l]>arr[maxindex]){
            maxindex = l;
        }
        if(r<length && arr[r]>arr[maxindex]){
            maxindex = r;
        }
        if(maxindex!=i){
            int temp = arr[i];
            arr[i] = arr[maxindex];
            arr[maxindex] = temp;
            adjustHeap(arr,maxindex,length);
        }
    }

    //构建小顶堆
    public void MinHeap(int[] arr){
        for(int i=arr.length/2 - 1; i>=0; i--){
            adjustminHeap(arr,i,arr.length);
        }
    }
    //调整小顶堆
    public void  adjustminHeap(int[] arr,int i,int length){
        int l = 2*i+1, r = 2*i+2, minindex=i;
        if(l<length && arr[l]<arr[minindex]){
            minindex = l;
        }
        if(r<length && arr[r]<arr[minindex]){
            minindex = r;
        }
        if(minindex!=i){
            int temp = arr[i];
            arr[i] = arr[minindex];
            arr[minindex] = temp;
            adjustHeap(arr,minindex,length);
        }
    }
}

 

五：交换排序

（1）冒泡排序

基本思想：

 

优化：（如果在某次排序中没有发生一次交换，就可以提前结束冒泡排序）

 （2）快速排序

基本思想：

class Solution {
    public int[] sortArray(int[] nums) {
        QuickSort(nums,0,nums.length-1);
        return nums;
    }
    public void QuickSort(int[] nums, int low, int high) {
        if(low<high){
            int i=low,j=high;
            int key = nums[i];
            while(i<j){
                while(i<j && nums[j]>=key) j--;
                if(i<j) nums[i] = nums[j];
                while(i<j && nums[i]<=key) i++;
                if(i<j) nums[j] = nums[i];
            }
            nums[i]=key;
            QuickSort(nums,low,i-1);
            QuickSort(nums,i+1,high);
        }
    }
}

 

六：归并排序

基本思想：归并排序采用了分治算法的思想：即 分：将待排序元素分成大小大致相同的2个子集合，再将子集合继续递归划分成更小的两个子集合，直到集合中只有一个元素；治：将子集两两合并成一个有序的集合，回溯直到合并成唯一的有序集合。

public class Main {
 
    public static void main(String[] args) {
        int[] arr = {11,44,23,67,88,65,34,48,9,12};
        int[] tmp = new int[arr.length];    //新建一个临时数组存放
        mergeSort(arr,0,arr.length-1,tmp);
        for(int i=0;i<arr.length;i++){
            System.out.print(arr[i]+" ");
        }
    }
    
    public static void merge(int[] arr,int low,int mid,int high,int[] tmp){
        int i = 0;
        int j = low,k = mid+1;  //左边序列和右边序列起始索引
        while(j <= mid && k <= high){
            if(arr[j] < arr[k]){
                tmp[i++] = arr[j++];
            }else{
                tmp[i++] = arr[k++];
            }
        }
        //若左边序列还有剩余，则将其全部拷贝进tmp[]中
        while(j <= mid){    
            tmp[i++] = arr[j++];
        }
        
        while(k <= high){
            tmp[i++] = arr[k++];
        }
        //将排好序的数据从temp中放回原数组对应位置中
        for(int t=0;t<i;t++){
            arr[low+t] = tmp[t];
        }
    }
 
    public static void mergeSort(int[] arr,int low,int high,int[] tmp){
        if(low<high){
            int mid = (low+high)/2;
            mergeSort(arr,low,mid,tmp); //对左边序列进行归并排序
            mergeSort(arr,mid+1,high,tmp);  //对右边序列进行归并排序
            merge(arr,low,mid,high,tmp);    //合并两个有序序列
        }
    }
    
}

 

七：基数排序（桶排序）

基本思想：它是这样实现的：将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后，数列就变成一个有序序列。换句话说，先找十个桶：0~9，第一轮按照元素的个位数排序，个位数是几就放入几号桶，全部放入完毕之后就从0号桶开始依次取出元素，便完成了对个位数的排序。之后继续按照十位，百位..排序，继续上述过程。

public class RadixSort {

    public static void main(String[] args) {
        int[] arr = new int[] { 23, 6, 9, 287, 56, 1, 789, 34, 65, 653 };
        System.out.println(Arrays.toString(arr));
        radixSort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void radixSort(int[] arr) {

        // 存数组中最大的数字,为了知道循环几次
        int max = Integer.MIN_VALUE;// (整数中的最小数)
        // 遍历数组，找出最大值
        for (int i = 0; i < arr.length; i++) {
            if (max < arr[i]) {
                max = arr[i];
            }
        }

        // 计算最大数是几位数
        int maxLength = (max + "").length();
        // 用于临时存储数据的数组（也就是桶，（0-9）10个桶，每个桶最多可以放入arr.length个元素）
        int[][] temp = new int[10][arr.length];
        // 用于存储桶内的元素个数，如counts[0]表示0号桶元素的个数。
        int[] counts = new int[10];

        // 第一轮个位数较易得到余数，第二轮就得先除以十再去取余，之后百位除以一百
        // 可以看出，还有一个变量随循环次数变化，为了取余

        // 循环的次数
        for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
            // 每一轮取余
            for (int j = 0; j < arr.length; j++) {
                // 计算余数
                int ys = (arr[j] / n) % 10;
                // 把数据放在对应桶中，有两个信息，放在第几个桶+数据应该放在桶里第几位
                temp[ys][counts[ys]] = arr[j];
                // 记录数量
                counts[ys]++;
            }

            // 记录从桶取出的数字应该放到位置
            int index = 0;
            // 每一轮循环之后挨个桶把数字取出来
            for (int k = 0; k < 10; k++) {
                // 如果桶中有元素就取出
                if (counts[k] != 0) {
                    for (int l = 0; l < counts[k]; l++) {
                        // 取出元素
                        arr[index] = temp[k][l];
                        index++;
                    }
                    // 取出后把数量置为零
                    counts[k] = 0;
                }
            }

        }
    }

}

复杂度分析：

 其中d是最大元素位数，r是基数（也就是桶数）(这里0-9，基数就是10)，n是数组元素个数。在基数排序中，因为没有比较操作，所以在复杂上，最好的情况与最坏的情况在时间上是一致的，均为 O(d * (n + r))。

 

 八：时间复杂度 与稳定性辅助记忆
时间复杂度：
冒泡、选择、直接 排序需要两个for循环，每次只关注一个元素，平均时间复杂度为O（n2）（一遍找元素O(n)，一遍找位置O(n)）
快速、归并、希尔、堆基于二分思想，log以2为底，平均时间复杂度为O(nlogn)（一遍找元素O(n)，一遍找位置O(logn)）

稳定性:“快希选堆”（快牺牲稳定性）

 

参考：https://www.bilibili.com/video/BV1E4411H73v?