【codeforces div3】【E. Cyclic Components】

E. Cyclic Components

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an undirected graph consisting of $\mathrm{nn vertices\; and mm edges.\; Your\; task\; is\; to\; find\; the\; number\; of\; connected\; components\; which\; are\; cycles.}$

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $\mathrm{aa is\; connected\; with\; a\; vertex bb,\; a\; vertex bb is\; also\; connected\; with\; a\; vertex aa).\; An\; edge\; can\text{'}t\; connect\; vertex\; with\; itself,\; there\; is\; at\; most\; one\; edge\; between\; a\; pair\; of\; vertices.}$

Two vertices $\mathrm{uu and vv belong\; to\; the\; same\; connected\; component\; if\; and\; only\; if\; there\; is\; at\; least\; one\; path\; along\; edges\; connecting uu and vv.}$

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

• the first vertex is connected with the second vertex by an edge,
• the second vertex is connected with the third vertex by an edge,
• ...
• the last vertex is connected with the first vertex by an edge,
• all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

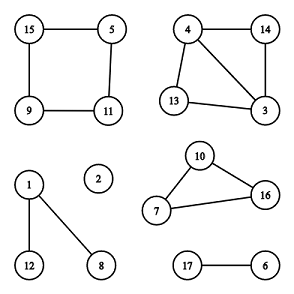
There are $\mathrm{66 connected\; components, 22 of\; them\; are\; cycles: [7,10,16][7,10,16] and [5,11,9,15][5,11,9,15].}$

Input

The first line contains two integer numbers $\mathrm{nn and mm (1\le n\le 2\cdot 1051\le n\le 2\cdot 105, 0\le m\le 2\cdot 1050\le m\le 2\cdot 105)\; —\; number\; of\; vertices\; and\; edges.}$

The following $\mathrm{mm lines\; contains\; edges:\; edge ii is\; given\; as\; a\; pair\; of\; vertices vivi, uiui (1\le vi,ui\le n1\le vi,ui\le n, ui\ne viui\ne vi).\; There\; is\; no\; multiple\; edges\; in\; the\; given\; graph,\; i.e.\; for\; each\; pair\; (vi,uivi,ui)\; there\; no\; other\; pairs\; (vi,uivi,ui)\; and\; (ui,viui,vi)\; in\; the\; list\; of\; edges.}$

Output

Print one integer — the number of connected components which are also cycles.

Examples

input

Copy

5 4
1 2
3 4
5 4
3 5

output

Copy

1

input

Copy

17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6

output

Copy

2

Note

In the first example only component $[3,4,5][3,4,5] is\; also\; a\; cycle.$

The illustration above corresponds to the second example.

题目大意：求单圈环的个数【单圈环就是只有一个圈的环...】

题目分析：观察单圈环的可以发现它的一个性质每个点的度都是2，所以

【方法一】只需要用dfs遍历一下所有连在一起点，查看点的度是不是为2

#include <bits/stdc++.h>
using namespace std;

#define f first
#define s second
#define ll long long
const int maxn=3e5;
vector<int>v[maxn];
int vis[maxn];
int ans,flag;
void dfs(int now,int fa)
{
    vis[now]=1;
    if(v[now].size()!=2)flag=1;
    for(auto i:v[now])
    {
    if(i==fa||vis[i])continue;
    dfs(i,now);
    }
}

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
    int x,y;
    cin>>x>>y;

    v[x].push_back(y);
    v[y].push_back(x);
    }
    for(int i=1;i<=n;i++)
    {
    flag=0;
    int ok=0;
    if(!vis[i])dfs(i,-1),ok=1;
    if(flag==0&&ok==1)ans++;
    }
    cout<<ans;
    return 0;
}

【方法二】

方法一中的dfs仅仅是寻找连在一起的点，其实寻找一个连通块连在一起的点只需要使用并查集就能解决，以下是并查集+判断度是不是为2

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
const int maxn=200005;
int fa[maxn];
vector<int>qwq[maxn];
vector<int>orz[maxn];
int find(int x)
{
    int xx=x;
    while(x!=fa[x])
    {
        x=fa[x];
    }
    while(fa[xx]!=x)
    {
        int t=fa[xx];
        fa[xx]=x;
        xx=t;
    }
    return x;
}
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i = 1 ; i <= n  ;i++)
    fa[i]=i;
    while(k--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        qwq[a].push_back(b);
        qwq[b].push_back(a);
        int qaq1=find(a);
        int qaq2=find(b);
        if(qaq1!=qaq2);
        fa[qaq1]=qaq2;
    }
    for(int i  = 1 ; i <= n  ; i++)
    {
        orz[find(i)].push_back(i);//利用连通块所有点的祖先来将联通块内部的点存在一起
    }
    int cnt=0;
    for(int i = 1 ; i <= n ; i++)
    {
        if(orz[i].size()>2)
        {
            bool or2=1;
            for(int j = 0 ; j < orz[i].size()&&or2;j++)
            {
                if(qwq[orz[i][j]].size()!=2)or2=0;
            }
            if(or2)cnt++;
        }
    }
    printf("%d\n",cnt);
    return 0;
}