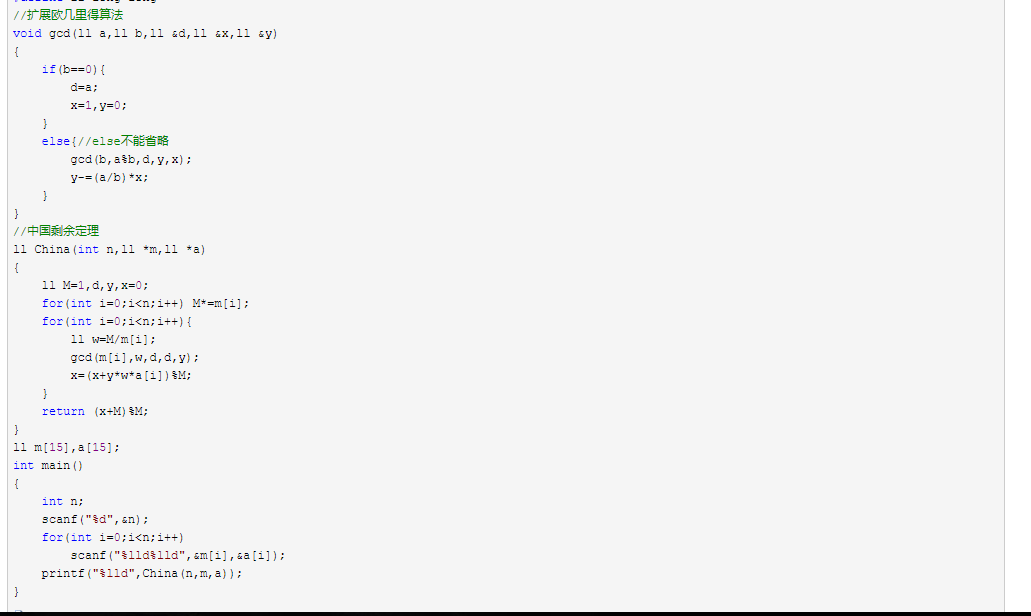
中国剩余定理（转载）（中国剩余定理与扩展欧几里德的联系）

https://www.cnblogs.com/freinds/p/6388992.html

首先要知道中国剩余定理是用来求 一个数 X 使 X%a=t1 && X%b=t2 && X%c=t3

具体操作是1）先求出 y3 * lcm(a,b)%c=1   y2 * lcm(a,c)%b=1  y1 * lcm(b,c)%a=1中的y1,y2,y3，也就是求lcm(a,b)关于模c的乘法逆元y3，求lcm(a,c)关于模b的乘法逆元y2，求lcm(b,c)关于模a的乘法逆元y1（其中lcm(a,b)是a和b的最小公倍数，而这里的abc互质，所以其实就是a*b）

　　　　　2）然后将这 y3*lcm(a,b)*t3+y2*lcm(a,c)*t2+y1*lcm(b,c)*t1

其中由于中国剩余定理第一步要求出乘法逆元，而求乘法逆元的方法正是扩展欧几里德定理 y3 * lcm(a,b)%c=1   y2 * lcm(a,c)%b=1  y1 * lcm(b,c)%a=1 ，由于abc互质，所以gcd=1，所以方程有解，且可使用扩展欧几里德算法求解