[hdoj5927][dfs]
http://acm.hdu.edu.cn/showproblem.php?pid=5927
Auxiliary Set
Time Limit: 9000/4500 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2991 Accepted Submission(s): 851
Problem Description
Given a rooted tree with n vertices, some of the vertices are important.
An auxiliary set is a set containing vertices satisfying at least one of the two conditions:
∙It is an important vertex
∙It is the least common ancestor of two different important vertices.
You are given a tree with n vertices (1 is the root) and q queries.
Each query is a set of nodes which indicates the unimportant vertices in the tree. Answer the size (i.e. number of vertices) of the auxiliary set for each query.
An auxiliary set is a set containing vertices satisfying at least one of the two conditions:
∙It is an important vertex
∙It is the least common ancestor of two different important vertices.
You are given a tree with n vertices (1 is the root) and q queries.
Each query is a set of nodes which indicates the unimportant vertices in the tree. Answer the size (i.e. number of vertices) of the auxiliary set for each query.
Input
The first line contains only one integer T (T≤1000), which indicates the number of test cases.
For each test case, the first line contains two integers n (1≤n≤100000), q (0≤q≤100000).
In the following n -1 lines, the i-th line contains two integers ui,vi(1≤ui,vi≤n) indicating there is an edge between uii and vi in the tree.
In the next q lines, the i-th line first comes with an integer mi(1≤mi≤100000) indicating the number of vertices in the query set.Then comes with mi different integers, indicating the nodes in the query set.
It is guaranteed that ∑qi=1mi≤100000.
It is also guaranteed that the number of test cases in which n≥1000 or ∑qi=1mi≥1000 is no more than 10.
For each test case, the first line contains two integers n (1≤n≤100000), q (0≤q≤100000).
In the following n -1 lines, the i-th line contains two integers ui,vi(1≤ui,vi≤n) indicating there is an edge between uii and vi in the tree.
In the next q lines, the i-th line first comes with an integer mi(1≤mi≤100000) indicating the number of vertices in the query set.Then comes with mi different integers, indicating the nodes in the query set.
It is guaranteed that ∑qi=1mi≤100000.
It is also guaranteed that the number of test cases in which n≥1000 or ∑qi=1mi≥1000 is no more than 10.
Output
For each test case, first output one line "Case #x:", where x is the case number (starting from 1).
Then q lines follow, i-th line contains an integer indicating the size of the auxiliary set for each query.
Then q lines follow, i-th line contains an integer indicating the size of the auxiliary set for each query.
Sample Input
1
6 3
6 4
2 5
5 4
1 5
5 3
3 1 2 3
1 5
3 3 1 4
Sample Output
Case #1:
3
6
3
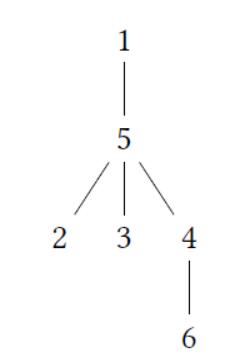 For the query {1,2, 3}:
•node 4, 5, 6 are important nodes For the query {5}:
•node 1,2, 3, 4, 6 are important nodes
•node 5 is the lea of node 4 and node 3 For the query {3, 1,4}:
• node 2, 5, 6 are important nodes
For the query {1,2, 3}:
•node 4, 5, 6 are important nodes For the query {5}:
•node 1,2, 3, 4, 6 are important nodes
•node 5 is the lea of node 4 and node 3 For the query {3, 1,4}:
• node 2, 5, 6 are important nodes
Hint
 For the query {1,2, 3}:
•node 4, 5, 6 are important nodes For the query {5}:
•node 1,2, 3, 4, 6 are important nodes
•node 5 is the lea of node 4 and node 3 For the query {3, 1,4}:
• node 2, 5, 6 are important nodes
For the query {1,2, 3}:
•node 4, 5, 6 are important nodes For the query {5}:
•node 1,2, 3, 4, 6 are important nodes
•node 5 is the lea of node 4 and node 3 For the query {3, 1,4}:
• node 2, 5, 6 are important nodes
Source
题意:给一棵树,给一堆定义,有q次查询
题解:dfs先跑出各个顶点的深度和父节点,然后给q次询问按照深度排序,最后在q次询问中更新当前顶点对父节点的影响。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define debug(x) cout<<"["<<#x<<"]"<<" "<<x<<endl; 5 const int maxn=1e5+5; 6 int head[maxn],cnt,fa[maxn],www[maxn],wwww[maxn],dep[maxn]; 7 struct edge{ 8 int to; 9 int nex; 10 int fr; 11 }e[maxn<<1]; 12 struct pot{ 13 int depth; 14 int id; 15 }p[maxn]; 16 void adde(int u,int v){ 17 e[cnt].fr=u; 18 e[cnt].to=v; 19 e[cnt].nex=head[u]; 20 head[u]=cnt++; 21 } 22 void dfs(int u,int f){ 23 fa[u]=f; 24 dep[u]=dep[f]+1; 25 wwww[u]=1; 26 for(int i=head[u];i!=-1;i=e[i].nex){ 27 int v=e[i].to; 28 if(v==f)continue; 29 dfs(v,u); 30 wwww[u]++; 31 } 32 } 33 bool cmp(struct pot aa,struct pot bb){ 34 return aa.depth>bb.depth; 35 } 36 int main() 37 { 38 int t; 39 scanf("%d",&t); 40 int ca=1; 41 while(t--){ 42 int n,q; 43 scanf("%d%d",&n,&q); 44 cnt=0; 45 for(int i=1;i<=n;i++){ 46 head[i]=-1; 47 wwww[i]=0; 48 } 49 for(int i=1;i<n;i++){ 50 int x,y; 51 scanf("%d%d",&x,&y); 52 adde(x,y); 53 adde(y,x); 54 } 55 dfs(1,0); 56 printf("Case #%d:\n",ca++); 57 for(int i=1;i<=q;i++){ 58 int w; 59 scanf("%d",&w); 60 for(int j=1;j<=w;j++){ 61 scanf("%d",&p[j].id); 62 p[j].depth=dep[p[j].id]; 63 } 64 int ans=n; 65 sort(p+1,p+1+w,cmp); 66 for(int j=1;j<=w;j++){ 67 int v=p[j].id; 68 www[v]++; 69 if(wwww[v]==www[v]){ 70 www[fa[v]]++; 71 } 72 if(wwww[v]-www[v]<2){ans--;} 73 } 74 for(int j=1;j<=w;j++){ 75 int v=p[j].id; 76 www[v]=0; 77 www[fa[v]]=0; 78 } 79 printf("%d\n",ans); 80 } 81 } 82 return 0; 83 }


