题解 Luogu P4246 [SHOI2008]堵塞的交通

题意

给定 \(2 \times C\) 的网格图，初始网格图中没有边。要求支持 \(m\) 次操作，每次操作是以下三种之一：

• 在相邻两点之间连一条边
• 断掉相邻两点之间的边
• 询问两点是否连通

\(1 \leq C,m \leq 10^5\)

题解

线段树神题。

对于节点 \([l,r]\)，考虑维护左上 / 左下能不能通过区间内部的点到达右上 / 右下，以及左上和左下 / 右上和右下能不能相互到达。

为了方便起见，下面的代码中，将会用两个字母代表这两点是否连通。其中小写字母表示上方点，大写字母表示下方点，字母 L 或 l 表示左侧，字母 R 或 r 表示右侧。

struct Node{
	bool lr,LR,lR,Lr,lL,rR; // lower case: up upper case: down
	int Llim,Rlim; // 下文会解释这个东西的用处
}tree[N<<2];

接下来就是怎么写 pushup() 的问题。当我们合并两个区间的时候，对于任意两个点的联通情况都需要考虑两条路径：

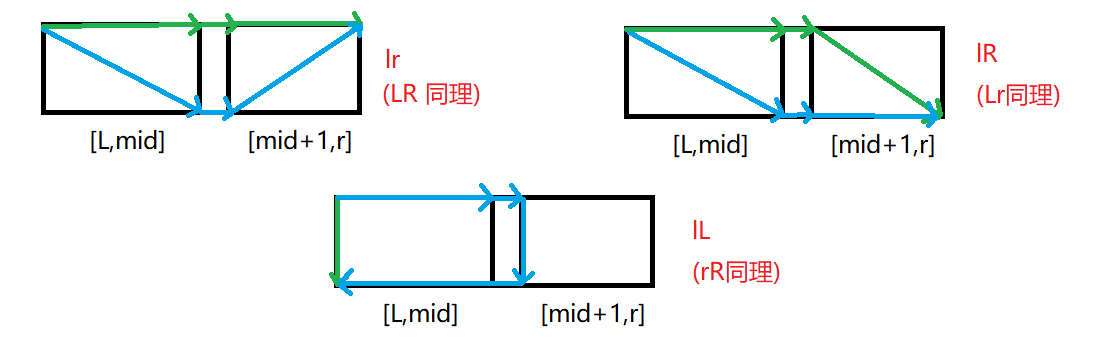
inline void pushup(Node &now,Node lc,Node rc){ // 将两个区间 lc,rc 合并为 now
    // Llim 和 Rlim 分别记录了区间的左右端点
	bool Umid=c[lc.Rlim][0],Dmid=c[lc.Rlim][1]; // 中间跨区间的边是否存在 c[x][0/1] 表示 x 连向 x+1 的上方 / 下方边是否存在
	now.Llim=lc.Llim,now.Rlim=rc.Rlim; 
	now.lr=(lc.lr&&Umid&&rc.lr)||(lc.lR&&Dmid&&rc.Lr);
	now.LR=(lc.LR&&Dmid&&rc.LR)||(lc.Lr&&Umid&&rc.lR);
	now.lL=lc.lL||(lc.lr&&Umid&&rc.lL&&Dmid&&lc.LR);
	now.rR=rc.rR||(rc.lr&&Umid&&lc.rR&&Dmid&&rc.LR);
	now.lR=(lc.lr&&Umid&&rc.lR)||(lc.lR&&Dmid&&rc.LR);
	now.Lr=(lc.LR&&Dmid&&rc.Lr)||(lc.Lr&&Umid&&rc.lr);
	return;
}

注意上图中的每一个箭头并不代表着一定要按照该箭头的走法。

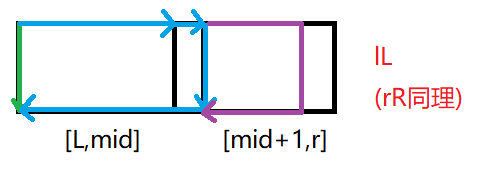
紫色箭头的走法也是对的，只不过殊途同归，就简化为了蓝色箭头。

接下来处理修改操作：如果修改操作是一条竖边，那么找到对应的叶子节点进行修改即可。

void changea(int k,int l,int r,int x,int v){
	if(l==r){
		tree[k].lL=tree[k].rR=tree[k].Lr=tree[k].lR=(bool)v;
        // 注意这里 l 和 r, L 和 R 是一个点，lr 和 LR 总是 true
		return;
	}
	int mid=(l+r)>>1;
	if(x<=mid)
		changea(lec(k),l,mid,x,v);
	else
		changea(rec(k),mid+1,r,x,v);
	pushup(tree[k],tree[lec(k)],tree[rec(k)]);
	return;
}

如果修改操作是一条横边，那么最先影响到的是以其为中点的区间。找到该区间进行修改即可。

void changeb(int k,int l,int r,int x,int UD,int v){
	int mid=(l+r)>>1;
	if(mid==x){
		c[x][UD]=v;
		pushup(tree[k],tree[lec(k)],tree[rec(k)]);
		return;
	}
	if(mid>x){
		changeb(lec(k),l,mid,x,UD,v);
	}else{
		changeb(rec(k),mid+1,r,x,UD,v);
	}
	pushup(tree[k],tree[lec(k)],tree[rec(k)]);
	return;
}

查询操作便体现了人类智慧。注意到，我们不仅可以通过区间内部，还可以在区间外部绕来绕去，如图：

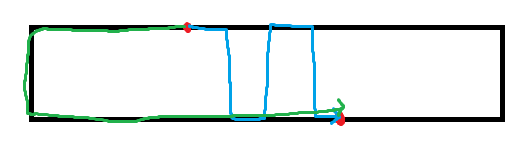
于是我们需要找出 \([1,l]\)，\([l,r]\)，\([r,C]\) 三个区间内部的答案，然后分类讨论，各四种情况：

• 两个点在同一行（以第一行举例）

  

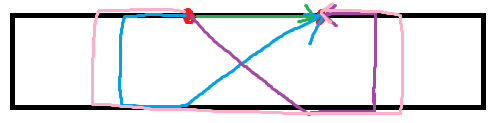
• 两个点不在同一行（以左上、右下举例）

  

完整代码：

# include <bits/stdc++.h>

const int N=100010,INF=0x3f3f3f3f;

struct Node{
	bool lr,LR,lR,Lr,lL,rR;
	int Llim,Rlim; // lower case: up upper case: down
}tree[N<<2];

int n;

bool c[N][2];

inline int read(void){
	int res,f=1;
	char c;
	while((c=getchar())<'0'||c>'9')
		if(c=='-')f=-1;
	res=c-48;
	while((c=getchar())>='0'&&c<='9')
		res=res*10+c-48;
	return res*f;
}
inline int lec(int x){
	return x<<1;
}
inline int rec(int x){
	return x<<1|1;
}
inline void pushup(Node &now,Node lc,Node rc){
	bool Umid=c[lc.Rlim][0],Dmid=c[lc.Rlim][1];
	now.Llim=lc.Llim,now.Rlim=rc.Rlim;
	now.lr=(lc.lr&&Umid&&rc.lr)||(lc.lR&&Dmid&&rc.Lr);
	now.LR=(lc.LR&&Dmid&&rc.LR)||(lc.Lr&&Umid&&rc.lR);
	now.lL=lc.lL||(lc.lr&&Umid&&rc.lL&&Dmid&&lc.LR);
	now.rR=rc.rR||(rc.lr&&Umid&&lc.rR&&Dmid&&rc.LR);
	now.lR=(lc.lr&&Umid&&rc.lR)||(lc.lR&&Dmid&&rc.LR);
	now.Lr=(lc.LR&&Dmid&&rc.Lr)||(lc.Lr&&Umid&&rc.lr);
	return;
}
void build(int k,int l,int r){
	tree[k].Llim=l,tree[k].Rlim=r;
	if(l==r){
		tree[k].lr=true,tree[k].LR=true;
		return;
	}
	int mid=(l+r)>>1;
	build(lec(k),l,mid),build(rec(k),mid+1,r);
	pushup(tree[k],tree[lec(k)],tree[rec(k)]);	
	return;
}
void changea(int k,int l,int r,int x,int v){
	if(l==r){
		tree[k].lL=tree[k].rR=tree[k].Lr=tree[k].lR=(bool)v;
		return;
	}
	int mid=(l+r)>>1;
	if(x<=mid)
		changea(lec(k),l,mid,x,v);
	else
		changea(rec(k),mid+1,r,x,v);
	pushup(tree[k],tree[lec(k)],tree[rec(k)]);
	return;
}
void changeb(int k,int l,int r,int x,int UD,int v){
	int mid=(l+r)>>1;
	if(mid==x){
		c[x][UD]=v;
		pushup(tree[k],tree[lec(k)],tree[rec(k)]);
		return;
	}
	if(mid>x){
		changeb(lec(k),l,mid,x,UD,v);
	}else{
		changeb(rec(k),mid+1,r,x,UD,v);
	}
	pushup(tree[k],tree[lec(k)],tree[rec(k)]);
	return;
}
Node query(int k,int l,int r,int L,int R){
	if(L<=l&&r<=R){
		return tree[k];
	}
	int mid=(l+r)>>1;
	if(L<=mid&&!(mid<R))
		return query(lec(k),l,mid,L,R);
	if(!(L<=mid)&&mid<R)
		return query(rec(k),mid+1,r,L,R);
	Node res,lres=query(lec(k),l,mid,L,R),rres=query(rec(k),mid+1,r,L,R);
	pushup(res,lres,rres);
	return res;
}

int main(void){
	n=read();
	build(1,1,n);
	char s[10];
	while(1){
		scanf("%s",s);
		if(s[0]=='E')
			break;
		int lx=read(),ly=read(),rx=read(),ry=read();
		if(ly>ry)
			std::swap(lx,rx),std::swap(ly,ry);
		if(s[0]=='O'||s[0]=='C'){
			if(ly==ry){
				changea(1,1,n,ly,s[0]=='O');
			}else{
				changeb(1,1,n,ly,lx-1,s[0]=='O');
			}
		}else{
			Node ansL=query(1,1,n,1,ly),ansMid=query(1,1,n,ly,ry),ansR=query(1,1,n,ry,n);
			bool ans=false;
			if(lx==1&&rx==1){
				ans=(ansMid.lr)||(ansL.rR&&ansMid.Lr)||(ansR.lL&&ansMid.lR)||(ansL.rR&&ansMid.LR&&ansR.lL);
			}
			if(lx==2&&rx==2){
				ans=(ansMid.LR)||(ansL.rR&&ansMid.lR)||(ansR.lL&&ansMid.Lr)||(ansL.rR&&ansMid.lr&&ansR.lL);
			}
			if(lx==1&&rx==2){
				ans=(ansMid.lR)||(ansL.rR&&ansMid.LR)||(ansR.lL&&ansMid.lr)||(ansL.rR&&ansMid.Lr&&ansR.lL);
			}
			if(lx==2&&rx==1){
				ans=(ansMid.Lr)||(ansL.rR&&ansMid.lr)||(ansR.lL&&ansMid.LR)||(ansL.rR&&ansMid.lR&&ansR.lL);
			}
			puts(ans?"Y":"N");
		}
	}
	return 0;
}