【瞎口胡】线段树优化建图
线段树优化建图用来优化一类区间连边的问题。
点向区间连边
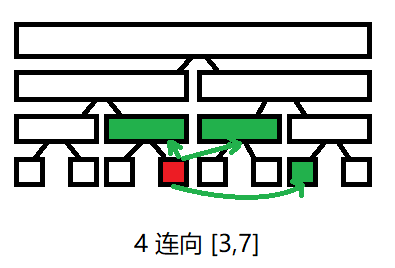
把区间拆成 \(\log\) 个线段树上的节点,然后连边即可。
线段树上的边含义是「可以从起点到达终点」。而能到达一个区间,自然也可以到达它的两个子区间,因此还需要补上这些边,即图中黑色边(注意黑边从上往下指)。
区间向点连边
类比一下上面。就是把边完全反向。
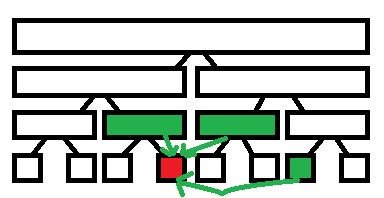
上图是 \([3,7]\) 连向 \(4\) 的情况。
注意此时黑边从下往上指,因为一个小区间没有向某个点连边并不代表这个区间不能到达该点,有可能存在包含它的一个大区间向该点连边。
区间向区间连边
如果只有一棵线段树,似乎不太好处理...考虑一下区间和区间本身的连边,除了连出一个自环之外没有任何用处。
我们换成两棵线段树试一试。其中一棵树为「入树」,作为连边的终点,与第一节中的线段树结构类似;另外一棵树为「出树」,作为连边的起点,与第二节中的线段树结构类似。
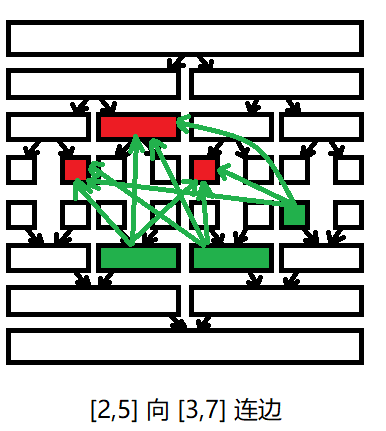
如图。上半部分是入树,下半部分是出树。要注意,两棵线段树的叶子节点其实是一个点。
但是这样,需要连 \(O(\log ^2n)\) 条边,不够优秀。考虑建立虚点,两棵树的点只与虚点相连:
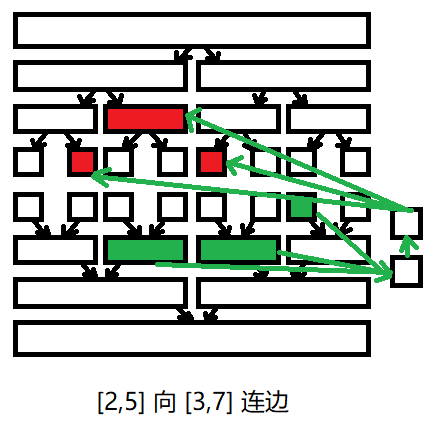
为什么是两个虚点,而不是一个?在部分题目中边带权,这个时候就需要给两个虚点相连的那条边赋上权值。
例题 1 Codeforces 786B Legacy
题意
给定 \(n\) 个点和 \(q\) 次操作。每次操作是下面三种类型之一:
-
给定 \(u,v,w\),连一条权值为 \(w\) 的有向边 \((u,v)\)
-
给定 \(l,r,v,w\),对于任意 \(u\) 满足 \(l \leq u \leq r\),连一条权值为 \(w\) 的有向边 \((u,v)\)
-
给定 \(l,r,u,w\),对于任意 \(v\) 满足 \(l \leq v \leq r\),连一条权值为 \(w\) 的有向边 \((u,v)\)
询问 \(s\) 到每个点的最短路,或者指除最短路不存在。
\(1 \leq n,q \leq 10^5, 1 \leq w \leq 10^9\)
题解
两棵线段树。一棵处理点向区间连边,另外一棵处理区间向点连边。当然,仍然需要注意两棵线段树的叶子节点其实是一个点。
# include <bits/stdc++.h>
typedef long long ll;
typedef std::pair <int,int> pii;
const ll INFll=0x3f3f3f3f3f3f3f3fll;
const int N=200010,MAXN=N*4,REF=N*2,INF=0x3f3f3f3f;
struct Node{
int id;
ll w;
bool operator < (const Node &rhs) const{
return w>rhs.w;
}
};
std::priority_queue <Node> q;
std::vector <pii> G[MAXN];
int n,m,s;
int id[N];
ll dis[MAXN];
bool c[MAXN];
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-')f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
inline void add(int u,int v,int w){
G[u].push_back(std::make_pair(v,w));
return;
}
inline int lc(int x){
return x<<1;
}
inline int rc(int x){
return x<<1|1;
}
void build(int k,int l,int r){
if(l==r){
id[l]=k;
add(k,k+REF,0),add(k+REF,k,0);
return;
}
int mid=(l+r)>>1;
add(k,lc(k),0),add(k,rc(k),0);
add(lc(k)+REF,k+REF,0),add(rc(k)+REF,k+REF,0);
build(lc(k),l,mid),build(rc(k),mid+1,r);
return;
}
void change(int k,int l,int r,int L,int R,int x,int w,int op){
if(L<=l&&r<=R){
(!op)?add(k+REF,id[x],w):add(id[x],k,w);
return;
}
int mid=(l+r)>>1;
if(L<=mid)
change(lc(k),l,mid,L,R,x,w,op);
if(mid<R)
change(rc(k),mid+1,r,L,R,x,w,op);
return;
}
inline void Dijkstra(void){
memset(dis,INF,sizeof(dis));
dis[s]=0;
q.push((Node){s,0});
while(!q.empty()){
int i=q.top().id;
q.pop();
if(c[i])
continue;
c[i]=true;
for(int j=0;j<(int)G[i].size();++j){
int to=G[i][j].first;
ll w=G[i][j].second;
if(dis[to]>dis[i]+w){
dis[to]=dis[i]+w,q.push((Node){to,dis[to]});
}
}
}
return;
}
int main(void){
n=read(),m=read(),s=read();
build(1,1,n);
for(int i=1;i<=m;++i){
int op=read(),v=read(),l,r,w;
switch(op){
case 1:{
l=read(),w=read(),add(id[v],id[l],w);
break;
}
case 2:{
l=read(),r=read(),w=read(),change(1,1,n,l,r,v,w,1);
break;
}
case 3:{
l=read(),r=read(),w=read(),change(1,1,n,l,r,v,w,0);
break;
}
}
}
s=id[s],Dijkstra();
for(int i=1;i<=n;++i){
printf("%lld ",dis[id[i]]==INFll?-1:dis[id[i]]);
}
return 0;
}
例题 2 [SNOI2017]炸弹
题意
给定坐标轴上 \(n\) 个炸弹的坐标和引爆半径,第 \(i\) 个炸弹的坐标为 \(x_i\),引爆半径为 \(r_i\)。
当一个炸弹被引爆时,它会引爆在爆炸范围内的所有炸弹,即满足 \(|x_i-x_j| \leq r_i\) 的所有炸弹 \(j\)。
你需要求出,对于每个炸弹,如果把它引爆,会有多少个炸弹被引爆。
\(1 \leq n \leq 5 \times 10^5, -10^{18} \leq x_i \leq 10^{18},0 \leq r_i \leq 2 \times 10^{18}\)
题解
注意到一个炸弹能引爆的炸弹一定是一段区间(不考虑二次引爆)。二分找到该区间的左右边界,然后线段树优化建图。
似乎可以对该图缩点后进行拓扑排序。把线段树上的叶子节点赋予点权 \(1\),求的就是一个点出发能到达的点权和。然而这不能做:
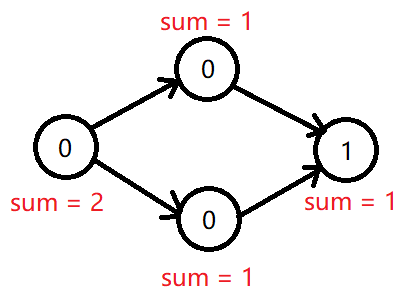
想象中的建反图拓扑排序效果如上图。最左侧的点答案会被错误地统计为 \(2\)。
观察到一个炸弹在考虑二次引爆的情况下,能引爆的炸弹也是一段区间。记录下每个点对应的区间,从而可以在缩点时求出每一个强连通分量对应的区间。
之后建反图拓扑排序,维护每个点对应区间的左端点和右端点即可。
# include <bits/stdc++.h>
typedef long long ll;
const int N=500010,MAXN=N*4,INF=0x3f3f3f3f;
const ll MOD=1e9+7;
struct Edge{
int to,next;
};
struct Graph{
Edge edge[N*20];
int head[MAXN],sum;
inline void add(int x,int y){
edge[++sum].to=y;
edge[sum].next=head[x];
head[x]=sum;
return;
}
}A,B;
int n;
ll x[N],R[N];
int id[N];
int nL[MAXN],nR[MAXN];
int maxid;
int col[MAXN],colcnt,t,dfn[MAXN],low[MAXN],cL[MAXN],cR[MAXN],du[MAXN];
bool vis[MAXN];
std::stack <int> K;
inline ll read(void){
ll res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-')f=-1;
res=c-48ll;
while((c=getchar())>='0'&&c<='9')
res=res*10ll+c-48;
return res*f;
}
inline int lc(int x){
return x<<1;
}
inline int rc(int x){
return x<<1|1;
}
inline void ckmin(int &x,int val){
x=std::min(x,val);
}
inline void ckmax(int &x,int val){
x=std::max(x,val);
return;
}
void build(int k,int l,int r){
ckmax(maxid,k);
nL[k]=l,nR[k]=r;
if(l==r){
id[l]=k;
return;
}
int mid=(l+r)>>1;
A.add(k,lc(k)),A.add(k,rc(k));
build(lc(k),l,mid),build(rc(k),mid+1,r);
return;
}
void change(int k,int l,int r,int L,int R,int x){
if(L<=l&&r<=R){
if(k!=x)
A.add(x,k);
return;
}
int mid=(l+r)>>1;
if(L<=mid)
change(lc(k),l,mid,L,R,x);
if(mid<R)
change(rc(k),mid+1,r,L,R,x);
return;
}
void tarjan(int i){
dfn[i]=low[i]=++t,K.push(i),vis[i]=true;
for(int j=A.head[i];j;j=A.edge[j].next){
int to=A.edge[j].to;
if(!vis[to]&&dfn[to])
continue;
if(!dfn[to])
tarjan(to),low[i]=std::min(low[i],low[to]);
else
low[i]=std::min(low[i],dfn[to]);
}
if(dfn[i]==low[i]){
++colcnt;
while(K.top()!=i){
int x=K.top();
K.pop(),vis[x]=false,col[x]=colcnt;
ckmin(cL[colcnt],nL[x]),ckmax(cR[colcnt],nR[x]);
}
K.pop(),vis[i]=false,col[i]=colcnt;
ckmin(cL[colcnt],nL[i]),ckmax(cR[colcnt],nR[i]);
}
return;
}
inline void topsort(void){
std::queue <int> q=std::queue <int> ();
for(int i=1;i<=n;++i){
if(!du[i])
q.push(i);
}
while(!q.empty()){
int i=q.front();
q.pop();
for(int j=B.head[i];j;j=B.edge[j].next){
int to=B.edge[j].to;
--du[to],ckmin(cL[to],cL[i]),ckmax(cR[to],cR[i]);
if(!du[to])
q.push(to);
}
}
return;
}
int main(void){
n=read();
build(1,1,n);
for(int i=1;i<=n;++i)
x[i]=read(),R[i]=read();
for(int i=1;i<=n;++i){
int l=std::lower_bound(x+1,x+1+n,x[i]-R[i])-x,r=std::upper_bound(x+1,x+1+n,x[i]+R[i])-x-1;
if(l<=r)
change(1,1,n,l,r,id[i]);
}
memset(cL,INF,sizeof(cL)),memset(cR,-INF,sizeof(cR));
for(int i=1;i<=maxid;++i)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=maxid;++i){
for(int j=A.head[i];j;j=A.edge[j].next){
int to=A.edge[j].to;
if(col[i]!=col[to]){
B.add(col[to],col[i]),++du[col[i]];
}
}
}
topsort();
ll ans=0;
for(int i=1;i<=n;++i){
ans=(ans+1ll*i*(cR[col[id[i]]]-cL[col[id[i]]]+1))%MOD;
}
printf("%lld",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号