【瞎口胡】二分图
二分图,即满足以下条件的图 \(G(V,E)\):
- 存在 \(V\) 的两个子集 \(A,B\) 满足 \(A \cup B = V\)
- \(E\) 中不存在边 \((u,v)\) 使得 \(u \in A,v \in B\)
直观上讲,就是这个图可以分成两列点,每一列点之间没有连边,边由一列点连向另外一列点。
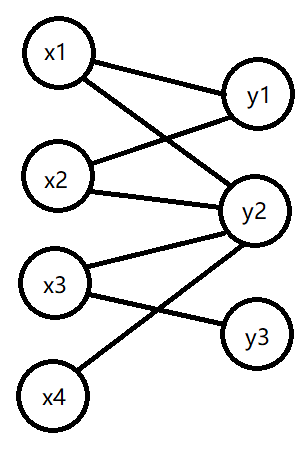
二分图判定
任选一个点为起点开始 DFS,将起点标为黑色。按照如下策略遍历每条边:
- 如果该边的终点没有访问过,将它的颜色标为当前点相反的颜色,并转到该点继续 DFS。
- 如果该边的终点有颜色且和当前点相同,那么该图不为二分图。
在图不连通时,要求每个连通块都要成功染色。
这样,颜色相同的点在同一列,就构成了一个二分图。
// vst ... visit
void dfs(int i,int colors){
if(vst[i]&&colors!=color[i]){
printf("Impossible");
exit(0);
return;
}
if(vst[i])
return;
vst[i]=true;
color[i]=colors;
++(colors==0?whitesum:blacksum);
for(rr int j=head[i];j;j=edge[j].next){
dfs(edge[j].to,!colors);
}
return;
}
二分图匹配
在二分图中选出一些边,这些边的端点不相同,这就构成了二分图的一个匹配。边的数量就是这个匹配的大小。
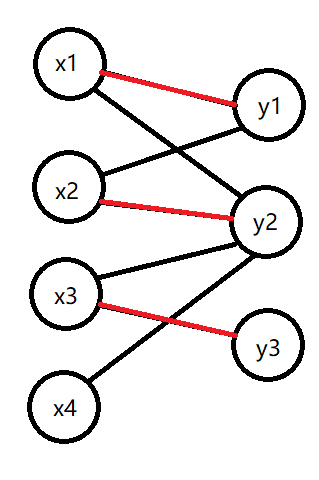
红边即为二分图的匹配,大小为 \(3\)。同时,这是该二分图的最大匹配。红边为该匹配的匹配边,黑边为该匹配的非匹配边。
二分图最大匹配 · 匈牙利算法
定义二分图的交互道路为红边与黑边交互出现的路径,且路径起点在左侧,终点在右侧。
增广路为路径起点、终点为非匹配点的交互道路。
观察到,将增广路上的每一条边颜色取反(红、黑)互换,匹配边增加一条,匹配的大小增加 \(1\)。匈牙利算法就是不断地寻找增广路,直到图中不存在增广路为止。
当图中不存在增广路时,我们找到了该图的最大匹配。
证明如下:
- 有增广路的匹配一定不是最大匹配,因为可以红黑边互换颜色。
- 没有增广路的匹配一定是最大匹配。考虑一个没有增广路的匹配 \(M\) 和一个最大匹配 \(M'\)。构造图 \(G=M \oplus M'\)。令 \(G\) 中属于 \(M\) 的边为 \(0\) 边,属于 \(M'\) 的边为 \(1\) 边,那么图中存在一些 \(0,1\) 交替且 \(0,1\) 边数量相等的交互道路。如果 \(0,1\) 边不等,图中存在至少一条增广路,与假设矛盾。将 \(1\) 边加入 \(M\),\(0\) 边从 \(M\) 中删除,就把 \(M\) 转换为了 \(M'\)。因为 \(0,1\) 边数量相等,所以这样做不会使匹配的大小变化。
综上,没有增广路是该匹配为最大匹配的充分必要条件。
匈牙利算法的流程是:
- 清空所有 \(vis\) 标记。
- 找到左侧一个没有被匹配的点 \(x_i\)。
- 找一条非匹配边 \((x_i,y_i)\),且 \(y_i\) 没有 \(vis\) 标记。对 \(y_i\) 打上 \(vis\) 标记。
- 如果 \(y_i\) 不在匹配中,将 \(x_i\) 和 \(y_i\) 匹配。
- 如果 \(y_i\) 在匹配中,转到与 \(y_i\) 匹配的点 \(x_j\) 并重复步骤 \(2\),直到找到一个没有匹配的 \(y_i\) 或者无路可走。如果找到了这样的 \(y_i\),将路径上的所有边反色,就得到了一个比原来大 \(1\) 的匹配。
重复执行上面流程,直到所有 \(x_i\) 点作为起点执行过一次算法。此时图中不存在增广路,找到了一个最大匹配。
为什么要对 \(y_i\) 打上 \(vis\) 标记?因为每一次进入 \(y_i\) 所做的操作都是相同的,如果第一次没有找到增广路,再进一次也不会找到。
最坏情况下,每次搜索都会遍历所有点和所有边,因此时间复杂度为 \(O(n^2m)\)。
模板 Luogu P3386 Code
# include <bits/stdc++.h>
const int N=510,M=50010;
struct Edge{
int to,next;
}edge[M];
int head[N],sum;
int n,m,e;
int vis[N],clo,link[N];
inline void add(int x,int y){
edge[++sum].to=y;
edge[sum].next=head[x];
head[x]=sum;
return;
}
bool dfs(int i){
for(int j=head[i];j;j=edge[j].next){
int to=edge[j].to;
if(vis[to]==clo)
continue;
vis[to]=clo;
if(!link[to]||dfs(link[to])){
link[to]=i;
return true;
}
}
return false;
}
int main(void){
scanf("%d%d%d",&n,&m,&e);
for(int i=1;i<=e;++i){
int u,v;
scanf("%d%d",&u,&v),add(u,v);
}
int ans=0;
for(int i=1;i<=n;++i){
clo=i;
ans+=dfs(i);
}
printf("%d",ans);
return 0;
}
二分图的部分定理
最小点覆盖与最大独立集
在二分图中,选出一个点集,使得每条边至少有一个端点在这个点集中,则该点集被称为该二分图的点覆盖。点集大小最小的点覆盖被称为最小点覆盖。
在二分图中,选出一个点集,使得该点集两两没有边,则该点集被称为该二分图的独立集。
Konig 定理:二分图的最小点覆盖 = 最大匹配(设最大匹配大小为 \(k\))。
-
证明
首先,二分图的最小点覆盖 \(\geq k\),这是因为最大匹配中每条边的两个端点至少有一个要被选中。接下来,我们可以构造出一个大小为 \(k\) 的点覆盖。
任取一个原图的最大匹配,从原图中右侧的非匹配点开始 DFS,交替着走非匹配边和匹配边,将所有经过的点打上标记,那么左侧被标记的点和右侧没有被标记的点构成一个点覆盖。接下来,我们来证明它。
首先,右侧不存在一个非匹配点没有被标记(它会作为 DFS 起点),且左侧不存在一个非匹配点被标记(否则找到增广路)。这样,左侧被标记的点和右侧没有被标记的点都是匹配点。
其次,对于任意一个匹配,按照 DFS 的要求,要么两个端点都没有被标记,要么两个端点都被标记。这样,每个匹配中有且仅有一个点会被选入该点覆盖,一共 \(k\) 个。
最后,不存在一条边,它的两端都没有被选入该点覆盖中。出现此情况时,该边一定左侧没有被标记且右侧被标记。根据上文,该边一定不是匹配边,这样,右侧被打上标记时一定会走这条非匹配边到左侧(因为 DFS 从右侧出发走交替路,那么从右到左走的是非匹配边,从左到右走的时匹配边),从而左侧被打上标记。综上,这种边不存在。
于是我们得到了一个大小为 \(k\) 的点覆盖,证毕。
Konig 定理的推论:二分图的最大独立集大小等于点数减去最小点覆盖数。
-
证明
除了最小点覆盖之外的其它点,就是最大独立集。如果这些点之中存在两个点有边,那么说明最小点覆盖不是一个点覆盖。同时注意到,最大独立集大小显然不能大于点数减去最小点覆盖数,否则最小点覆盖可以更小。


