【瞎口胡】Tarjan 算法

Tarjan 是求解图连通分量的一种算法。

其应用范围有无向图和有向图两个。

无向图的 Tarjan 算法

基本定义

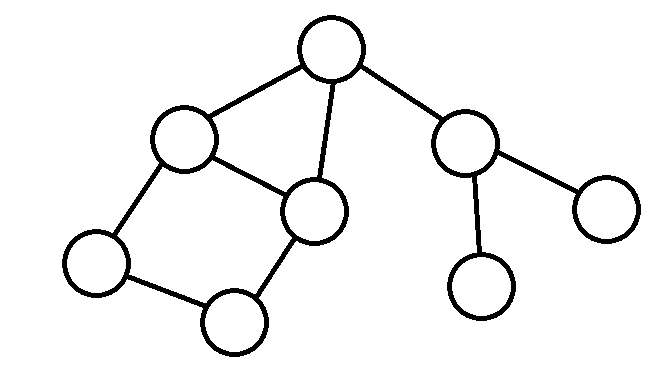
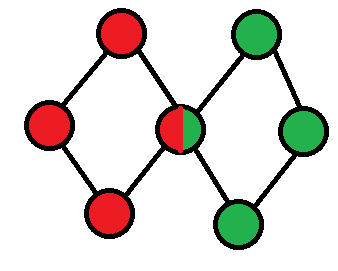
对于像上图中的无向连通图，从任意节点出发 DFS 遍历图，经过的边构成一棵原图的 DFS 树。如果图不连通，需要对每一个连通块进行 DFS，得到一个 DFS 森林。DFS 森林即为若干棵 DFS 树，接下来我们只讨论连通图的处理。

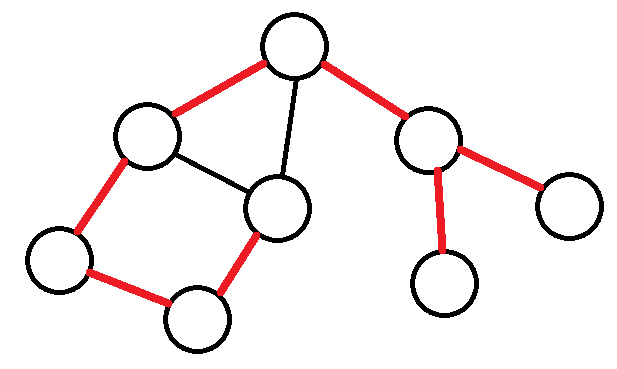
图中的红边构成原图的 DFS 树。

我们定义 \(dfn_i\) 表示节点 \(i\) 被访问到的先后顺序，如果节点 \(i\) 第 \(x\) 个被访问到，则 \(dfn_i=x\)。\(dfn_i\) 还有一个名字叫做「时间戳」。定义 \(\text{subtree}(x)\) 表示 \(x\) 的子树中的节点。

那么原图中的边可以分为两类：

• 树边，即 DFS 树上的边。

  树边的两个端点存在父子关系。

• 返祖边，即不在 DFS 树上的边。

  一切不在 DFS 树上的边都是返祖边。返祖边的两个端点存在祖孙关系。

  证明：因为进行的是 DFS，所以对于每个端点，必然会从它出发遍历所有与之相连且没有被访问过的节点。假设一条边的两个端点 \(u,v(dfn_u < dfn_v)\) 不存在祖孙关系（既不是树边也不是返祖边），那么 \(v\) 的父亲不是 \(\text{subtree}_u\) 中的任何一个节点，而是 \(u\) 的某位祖先。此时对于 \(u\)，它没有出发遍历与其相连的 \(v\) 而是退出了 DFS，显然不符合 DFS 遍历图的要求。所以不存在这样的边。

除此之外，我们还定义节点 \(i\) 「追溯值」 \(low_i\) 为以下节点的时间戳的最小值：

• 在 \(i\) 子树中的节点。
• 从 \(i\) 出发走向 \(\text{subtree}_i\)，经过若干条树边后再经过至多一条返祖边能到达的节点。

令 \(low_i = dfn_i\)。然后遍历所有与之相连的边 \((i,x)\)。

• 如果 \((i,x)\) 是树边，令 \(low_i = \min\{low_i,low_x\}\)，因为从 \(i\) 到 \(x\) 不需要经过返祖边。
• 如果 \((i,x)\) 是返祖边，令 \(low_i = \min\{low_i,dfn_x\}\)，此时经过了一条返祖边，所以最多只能到达 \(x\)，不能到达 \(x\) 的祖先，故取 \(dfn_x\) 而非 \(low_x\)。

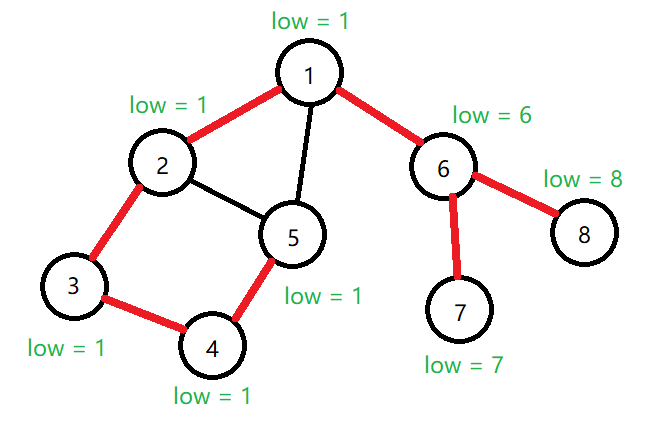
下图中，圆圈内标注了节点的时间戳，而圆圈外标注了节点的 \(low\) 值。

割边（桥）判定

若原图删去边 \((u,v)\) 后分裂成不相连的两个子图，则称 \((u,v)\) 是原图的一条割边，也称作「桥」。

容易发现，割边一定是搜索树上的边，且桥不在任何一个简单环上。接下来，我们只讨论搜索树上的边。

\((u,v)\) 是割边，当且仅当 \(u\) 是 \(v\) 的祖先，且 \(dfn_u < low_v\)。

证明：一个节点每经过一次返祖边，深度至少减小 \(1\)。若 \(dfn_u \geq low_v\)，则说明 \(v\) 可以通过另外一条返祖边到达 \(u\) 及 \(u\) 的祖先而不必经过 \((u,v)\)，删去 \((u,v)\) 不影响原图连通性，故 \((u,v)\) 不是割边。反之则 \(v\) 只能到达 \(u\) 的子树（不含 \(u\)），此时 \((u,v)\) 为割边。

在具体的题目中，可能有多条相同的边 —— 此时 \((u,v)\) 不一定为割边。为了避免这种情况，在代码实现中记录自己的父亲和自己的连边 \((fa,i)\) 的编号，遍历与 \(i\) 相连的所有边时，避开 \((fa,i)\) 的反向边即可。

小技巧：我们将边从 \(2\) 开始标号。编号为 \(2\) 和 \(3\) 的两条有向边表示一条无向边，\(4\) 和 \(5\) 表示一条无向边，\(6\) 和 \(7\) 表示一条无向边，...。观察到，将一条有向边的编号异或 \(1\) 则可以得到其反向边。

void tarjan(int i,int in_edge){ // 记录 (fa,i) 编号
	dfn[i]=low[i]=++t;
	for(rr int j=0;j<(int)G[i].size();++j){
		int to=G[i][j].first;
		if(!dfn[to]){
			tarjan(to,G[i][j].second);
			low[i]=std::min(low[i],low[to]);
			if(low[to]>dfn[i]){
				ans.push_back(std::make_pair(std::min(i,to),std::max(i,to)));
			}
		}else if(in_edge!=(G[i][j].second^1)){ // 只经过返祖边 避开 (i,fa) 这条树边
			low[i]=std::min(low[i],dfn[to]);
		}
	}
	return;
}

割点判定

若原图删去点 \(u\) 和与其相连的所有边后分裂成不相连的多个子图，则称 \(u\) 是原图的一个割点。

\(x\) 为割点，当且仅当存在 DFS 树上的边 \((x,y)\)，使得 \(dfn_x \leq low_y\)。

证明：考虑在无向图的搜索树中，一个节点 \(k\) 经过一条边要么到达 \(\text{subtree_k}\)，要么到达自己的祖先。如果上式成立，则 \(y\) 无法到达 \(x\) 的祖先。将 \(x\) 点删除后，原图不再连通。

在求割点时，我们不需要考虑返祖边，只需要考虑搜索树上的边（当前点的儿子）。

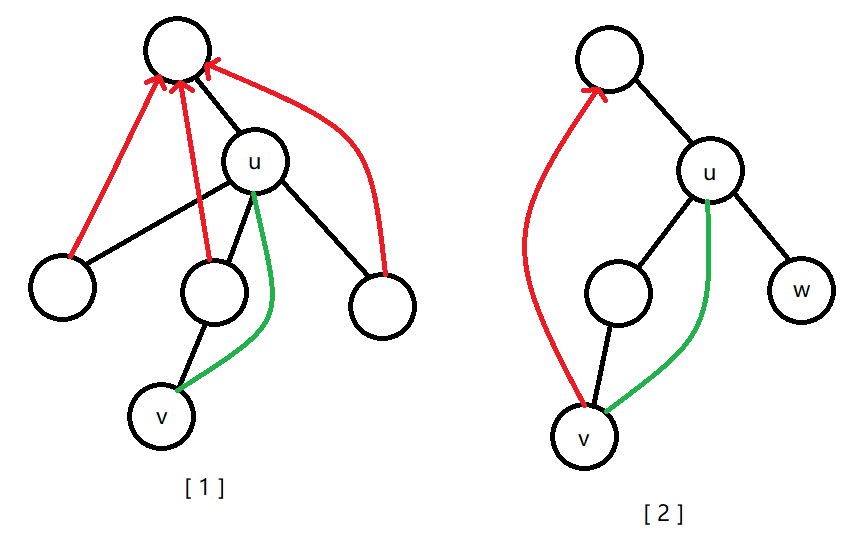
图 \([1]\) 中，\(u\) 的所有子节点都可以到达 \(u\) 的祖先，故 \(u\) 自然不是割点，此时不用考虑 \((u,v)\)。图 \([2]\) 中，\(u\) 的子节点 \(w\) 无法到达 \(u\) 的祖先，故 \(u\) 是割点，仍然不用考虑 \((u,v)\)。

特殊地，如果 \(u\) 是搜索树的根，当且仅当 \(u\) 有两棵及以上子树时 \(u\) 为割点，不能使用上述判定方法。

因为割点的判定时 \(dfn_x \leq low_y\) 而非 \(dfn_x < low_y\)，所以我们用父节点的 \(dfn\) 值更新 \(low\) 也是正确的。故求割点时，不用考虑重边和父节点的连边，因此可以简化代码。

模板题目：Luogu P3388

# include <bits/stdc++.h>

const int N=20010,INF=0x3f3f3f3f;

std::vector <int> G[N],ans;
int n,m;
int root;
int low[N],dfn[N],t;
int cut[N];
inline int read(void){
	int res,f=1;
	char c;
	while((c=getchar())<'0'||c>'9')
		if(c=='-')f=-1;
	res=c-48;
	while((c=getchar())>='0'&&c<='9')
		res=res*10+c-48;
	return res*f;
}
void tarjan(int i){
	low[i]=dfn[i]=++t;
	int subtree=0;
	for(int j=0;j<(int)G[i].size();++j){
		int to=G[i][j];
		if(!dfn[to]){
			tarjan(to);
			low[i]=std::min(low[i],low[to]);
			if(i==root)
				++subtree;
			if(dfn[i]<=low[to]&&i!=root){
				cut[i]=true;
			}
		}else{
			low[i]=std::min(low[i],dfn[to]);
		}
	}
	if(i==root&&subtree>1){
		cut[i]=true;
	}
	return;
}
int main(void){
	n=read(),m=read();
	for(int i=1;i<=m;++i){
		int u=read(),v=read();
		G[u].push_back(v),G[v].push_back(u);
	}
	for(int i=1;i<=n;++i){
		if(!dfn[i])
			root=i,tarjan(i);
	}
	int tot=0;
	for(int i=1;i<=n;++i){
		if(cut[i]){
			++tot,ans.push_back(i);
		}
	}
	printf("%d\n",tot);
	for(int i=0;i<(int)ans.size();++i){
		printf("%d ",ans[i]);
	}
	return 0;
}

点双连通分量 v-DCC 判定

在无向图中，没有割点的极大连通子图被称作原图的一个点双连通分量，简称 v-DCC。单独的一个点也是 v-DCC，这个比较特殊。可以根据题目的具体要求来判断。

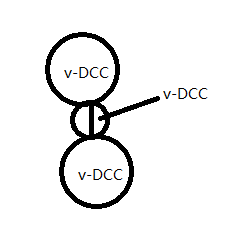
如上图，一个割点可以属于多个 v-DCC。

在 Tarjan 的时候可以把这个东西算出来。遍历到每个点的时候，将该点入栈。考虑对于点 \(x\)，如果它的一个儿子 \(y\) 满足 \(low_y \geq dfn_x\)，那么 \(y\) 不可能和 \(x\) 的祖先构成双连通分量（\(y\) 无法经过返祖边，因此到 \(x\) 的祖先必然经过 \(x\)，而 \(x\) 要么为割点要么为搜索树的根，与 v-DCC 定义矛盾）。此时将栈中（\(\text{subtree}_{y}\)）到 \(x\) 的所有节点构成新的 v-DCC。将栈顶到 \(x\)（不含 \(x\)）的所有节点出栈。

为什么 \(x\) 不能出栈呢？因为 \(x\) 此时要么是搜索树的根要么是割点（如果忘记了割点的判定，可以往上翻，和这里的判定方法一致）。\(x\) 有可能 和 \(x\) 的祖先再组成一个 v-DCC。

以上面的图为例，将原图标上 \(low\) 和 \(dfn\)。

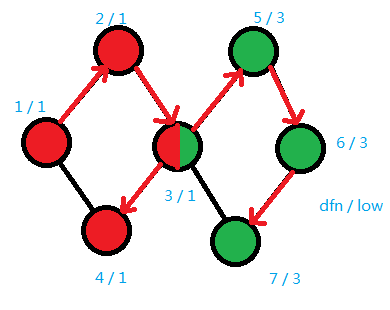
图中的 v-DCC 为 \((1,2,3,4)\) 和 \((3,5,6,7)\)。红色的 v-DCC 的判定为 \(low_2 \geq dfn_1\)，绿色的 v-DCC 判定为 \(low_5 \geq dfn_3\)。如果在判定绿色 v-DCC 时就把 \(3\) 出栈，红色的 v-DCC 就会少一个点 \(3\)。因此 v-DCC 的「根」不能出栈。在 Tarjan 结束后栈中只会剩下搜索树的根，如果有多组数据或者图不连通则需要手动把这个点清除掉。

void tarjan(int i){
	dfn[i]=low[i]=++tot; // 时间戳标号
	k.push(i);
	int ch=0; // 子树数量
	for(int j=head[i];j;j=edge[j].next){
		int to=edge[j].to;
		if(!dfn[to]){
			tarjan(to),++ch,low[i]=std::min(low[i],low[to]);
			if(low[to]>=dfn[i]){
				if(i!=1) // 割点判定
					cut[i]=true;
				++cnt; // 新的 v-DCC
				DCC[cnt].resize(0);
				DCC[cnt].push_back(i); // 放入根
				int now=0;
				while(1){
					now=k.top();
					k.pop();
					DCC[cnt].push_back(now);
					if(now==to) break; // to 是点双连通分量中除了 i 的最后一个点
				}
			}
		}else{
			low[i]=std::min(low[i],dfn[to]);
		}
	}
	if(ch>1&&i==1){ // 割点判定（默认搜索树根为 1）
		cut[i]=true;
	}
	return;
}

另外一篇文章中，我们发现，v-DCC 之间通过割点来连接。即：将原图中的 v-DCC 缩成一个新图，新图是若干个点没有边贴在一起的样子，结构与树较为相似。

下面来证明两个 v-DCC 如果连通，则一定存在至少一个公共点，这个公共点为割点。同时，从一个 v-DCC 的点到另外一个 v-DCC 的点，必然经过它们的公共点，而不是通过一条边跨越两个 v-DCC。

如果用图来说明的话，应该是这个样子：

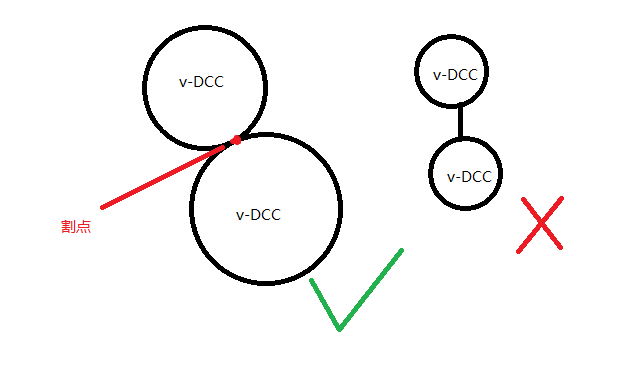
证明：右图边的两个端点一定是割点。如果它们不是割点，那么删掉其中的任意一个，图的连通性不变，那么该图属于同一个 v-DCC，与题意矛盾。因此，它们一定是割点，从而一定可以存在于同一个 v-DCC 当中（可以以这两个点构成一个 v-DCC），这样右图就变成了三个 v-DCC 通过这两个割点贴在一起的形态，仍然矛盾。因此右图中的这种情况不成立。

边双连通分量 e-DCC 判定

在无向图中，没有割边（桥）的极大连通子图被称作原图的一个边双连通分量，简称 e-DCC。单独的一个点也是 e-DCC，这个比较特殊。可以根据题目的具体要求来判断。

e-DCC 之间由割边（桥）来连接，仍然构成一棵树。这里的树就是货真价实的树了，有边连起来的那种。

在求割边（桥）的时候，我们稍作改动，就可以求出 e-DCC。这里我直接将无向边拆成两条有向边并在结构体中赋予它们相同的编号，避免从 DFS 树边返回父亲。没有使用编号异或 \(1\) 的技巧。

具体的求法为：和求 v-DCC 相同，节点第一次访问即入栈，当 \(low_i = dfn_i\) 时，将栈顶到 \(i\) 的所有点（包含 \(i\)）弹出。当 \(low_i = dfn_i\) 时，\(low_i > dfn_{fa}\)，其中 \(fa\) 为 \(i\) 的父亲，因此 \(fa \to i\) 为桥，这样 \(fa\) 及 \(i\) 的祖先无法和 \(i\) 组成 e-DCC，只能和栈中的节点一起组成 e-DCC。

void tarjan(int i,int in_edge){ // 记录树边的编号
	dfn[i]=low[i]=++cnt;
	k.push(i);
	for(int j=head[i];j;j=edge[j].next){
		int to=edge[j].to;
		if(!dfn[to]){
			tarjan(to,edge[j].id);
			low[i]=std::min(low[i],low[to]);
		}else if(edge[j].id!=in_edge){ // 如果编号相同 则为树边的反向边 不能用来更新
			low[i]=std::min(low[i],dfn[to]);
		}
	}
	if(dfn[i]==low[i]){
		++colcnt;
		col[i]=colcnt;
		while(k.top()!=i){
			col[k.top()]=colcnt,k.pop(); // 染色 相同颜色属于同一个 e-DCC
		}
		k.pop();
	}
	return;
}

有向图的 Tarjan 算法

基本定义

在有向图上进行 DFS，仍然可以得到一棵 DFS 树（或森林）。

原图的边 \((x,y)\) 可以分为四类：

• DFS 树边，此时 \(x\) 是 \(y\) 的父亲。
• 前向边，此时 \(x\) 是 \(y\) 的祖先。
• 返祖边，此时 \(y\) 是 \(x\) 的祖先。
• 横叉边，此时 \(x,y\) 没有祖孙关系，且 \(dfn_y < dfn_x\)，否则该边为树边。

在有向图的 Tarjan 算法中，\(dfn_i\) 的定义不变。

\(low_i\) 的定义为同时满足以下两个条件的节点的最小 \(dfn\) 值：

• 该节点在栈中。
• 存在一条从 \(\text{subtree}_i\) 出发的边，以其为终点。换言之，可以从 \(i\) 出发走向 \(\text{subtree}_i\)，经过若干条树边后再经过至多一条非树边到达该点。

求解 \(low_i\) 的过程：令 \(low_i = dfn_i\)，然后遍历与 \(i\) 有连接的点 \(x\)，若 \((i,x)\) 为树边（\(x\) 没有被访问过），令 \(low_i = \min\{low_i,low_x\}\)，否则令 \(low_i = \min\{low_i,dfn_x\}\)。

注意，我们要避开所有访问过且不在栈中的 \(x\)。用 \(in_x=1\) 或 \(0\) 记录节点 \(x\) 是否在栈中，则我们需要避开所有 \(dfn_x\) 已经被计算且 \(in_x=0\) 的点 \(x\)。

值得一提的是，不加区分 \((i,x)\) 是否为树边，直接写成 \(low_i = \min\{low_i,low_x\}\) 也是正确的写法。如果有人的 Tarjan 这么写，请不要怀疑它的正确性。

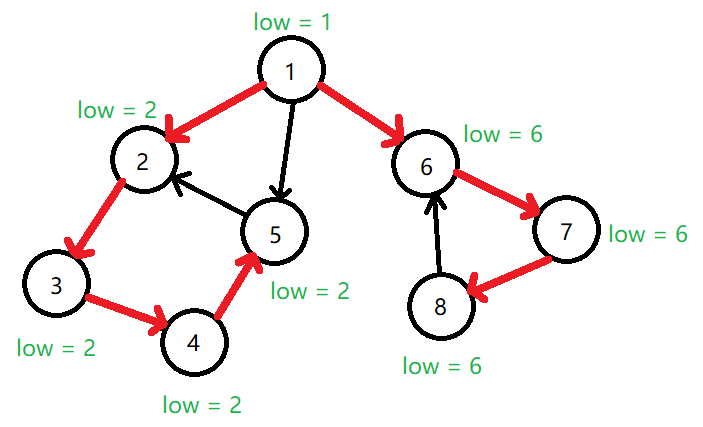
上图展示了每个节点的 \(dfn\) 值（圆圈内）和 \(low\) 值。

强连通分量判定

定义有向图 \(G(V,E)\) 的一个子图 \(G'(V',E')\) 是图 \(G\) 的一个强连通子图，当且仅当对于任意 \(i,j \in V\)，\(i\)，\(j\) 互相可达。\(G\) 的极大强连通子图称为「强连通分量」，简称 SCC。

考虑用栈记录仍然被搜索到，但没有找到自己所属连通分量的点。

每个强连通分量必然存在一个 \(dfn\) 值最小的点 \(rt\)，称之为「根」。\(rt\) 必然满足 \(dfn_{rt}=low_{rt}\)，此时栈顶到 \(rt\) 的所有节点组成一个强连通分量。

若 \(low_i = dfn_i\)，则说明：

• 不存在返祖边 \((j,fa) (j \in \text{subtree}_i)\)，这样 \(\text{subtree}_i\) 中的节点无法和其祖先构成环，进而无法和其祖先构成强连通分量。如果存在这样的边，\(fa \to i \to j \to fa\) 的路径构成了一个简单环。
• 不存在横叉边 \((j,x)(j \in \text{subtree}_i)\)，即 \(i\) 的子树中的节点无法到达时间戳更小的节点（因为横叉边的起点时间戳大于终点时间戳）。
• 前向边没有用，不用考虑。

故此时在栈中 \(\text{subtree}_i\) 的节点无法与其它节点构成强连通分量，只能独立构成一个强连通分量。

void tarjan(int i){
	low[i]=dfn[i]=++dfncount;
	vis[i]=true;
	k.push(i);
	for(rr int j=head[i];j;j=edge[j].next){
		int to=edge[j].to;
		if(!vis[to]&&dfn[to]){
			continue;
		}
		if(!dfn[to]){
			tarjan(to);
		}
		low[i]=std::min(low[i],low[to]);
		/* 上面 4 行的一个更规范的写法
		if(!dfn[to])
			tarjan(to),low[i]=std::min(low[i],low[to]);
		else
			low[i]=std::min(low[i],dfn[to]); 
		*/ 
	}
	if(low[i]==dfn[i]){ // 强连通分量的根
		++scccount; // 记录强连通分量数
		while(k.top()!=i){
			int u=k.top();
			vis[u]=false,col[u]=scccount,k.pop(); // 给强连通分量中的每个点染色
		}
		vis[i]=false,col[i]=scccount,k.pop(); // 不要忘了将它本身弹出去
	}
	return;
}

缩点

这里就简单地提一两句，不放代码了。

在求出每个点所属的 SCC 之后，保留原图中由一个 SCC 连向另外一个 SCC 的边，并将属于同一个 SCC 的所有点缩成一个，就构造出了一个新图，且该图为 DAG。DAG 有很多奇妙的性质，可以在上面拓扑排序，这对于某一类题很管用。

模板题 USACO 5.3 校园网络

应用题 JSOI2008 联通数 可以尝试大力缩点 + 建反图拓扑排序的 \(O(n^3)\) 或者 \(O(\frac{n^3}{64})\) 的 bitset 优化，可以起到练手的目的。

总结

其实 Tarjan 也就这样，很板子，看起来是好几个不同的部分，其实变通变通就行了。

重点在于应用和图论建模。有的时候还要和结论结合起来。这个就要靠平时积累了。