2020.08.08 / 09 模拟赛题解
08.07 的模拟赛因为版权原因没有办法公开。
Day 1 T1
题意
给定一棵二叉树,非叶节点的度数为 \(0\)。求最小的操作次数,每次操作交换一个非叶节点的两棵子树,来使左边的所有叶节点深度大于等于右边的叶节点,且叶节点的深度最大值和最小值之差不大于 \(1\)。
输入格式
第一行一个正整数 \(n\),表示非叶节点的数量。
第 \(2\) 至 \(n+1\) 行,第 \(i+1\) 行两个整数,表示节点 \(i\) 的左右两个儿子的编号。如果其儿子是叶节点,则编号为 \(-1\)。
输出格式
如果可能满足题目的条件,输出最小的操作次数,否则输出 \(-1\)。
对于 \(60\%\) 的数据,满足 \(1≤n≤20\)。
对于 \(100\%\) 的数据,满足 \(1≤n≤10^5\)。
\(60\) 分
观察到操作顺序不影响答案,\(O(2^n)\) 枚举每个节点是否交换子树,然后 \(O(n)\) 检查最终的树是否符合要求。
复杂度 \(O(2^n \times n)\)。
\(100\) 分
略复杂的分类讨论。
首先判断掉深度最大的叶节点和深度最小的叶节点深度差大于 \(1\) 的情况。因为交换子树不会影响叶节点深度,所以这种情况一定无解。
对于每个节点 \(i\),记 \(v_i\) 和 \(\text{maxdep}_i\)。其中,\(v_i=1\) 表示该节点为根的子树中所有节点深度都相等,否则 \(v_i=0\)。\(\text{maxdep}_i\) 表示该节点为根的子树中深度最大的叶节点。
考虑自底向下维护 \(v_i\),而 \(\text{maxdep}\) 在之前用一次 DFS 求出。对于每个非叶节点,设其左儿子为 \(L\),右儿子为 \(R\)。有几种可能的情况:
-
\(v_L=v_R=1,\text{maxdep}_L = \text{maxdep}_R\)
这种情况下,以 \(i\) 为根的子树中,叶节点深度完全相等。不需要任何操作。这种情况下,\(v_i=1\)。
对于以下情况,\(v_i\) 均为 \(0\)。
-
\(v_L=v_R=1,\text{maxdep}_L \neq \text{maxdep}_R\)
这种情况下,\(i\) 的左子树和右子树中,叶节点的深度完全相等,但 \(i\) 为根的子树并不。根据题意,如果 \(\text{maxdep}_L < \text{maxdep}_R\),则需要一次操作。
-
\(v_L=0,v_R=1\)
这种情况下,\(i\) 的右子树中叶节点深度完全相等,但左子树并不。如果 \(\text{maxdep}_L \leq \text{maxdep}_R\),那么需要一次操作。
-
\(v_L=1,v_R=0\)
这种情况下,\(i\) 的左子树中叶节点深度完全相等,但右子树并不。如果 \(\text{maxdep}_L < \text{maxdep}_R\),那么需要一次操作。
-
\(v_L=v_R=1\)
这种情况下,\(i\) 的左右子树中叶节点深度均不完全相等,根据题意,这是无解的。
时间复杂度 \(O(n)\)。
# include <bits/stdc++.h>
# define rr
const int N=500010,INF=0x3f3f3f3f;
int son[N][2];
int ans;
int m;
int n;
int maxdep[N],depth[N];
int allmax;
bool leaf[N],bad[N]; // bad 即为上文中的 v_i
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-')f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
void dfs(int i,int fa){
depth[i]=maxdep[i]=depth[fa]+1;
allmax=std::max(allmax,depth[i]);
if(leaf[i])
return;
for(rr int j=0;j<=1;++j){
int to=son[i][j];
if(to==fa)
continue;
dfs(to,i);
maxdep[i]=std::max(maxdep[i],maxdep[to]);
}
return;
}
void solve(int i,int fa){
if(leaf[i])
return;
for(rr int j=0;j<=1;++j){
solve(son[i][j],i);
}
if(bad[son[i][0]]&&bad[son[i][1]]){ // 完全相等
printf("-1"),exit(0);
}
if(!bad[son[i][0]]&&!bad[son[i][1]]){ // 无解
if(maxdep[son[i][0]]==maxdep[son[i][1]])
return;
else
bad[i]=true,ans+=((maxdep[son[i][0]]<maxdep[son[i][1]]));
return;
}
if(bad[son[i][0]]&&maxdep[son[i][0]]<=maxdep[son[i][1]])
++ans;
if(bad[son[i][1]]&&maxdep[son[i][1]]>maxdep[son[i][0]])
++ans;
bad[i]=true;
return;
}
int main(void){
// freopen("mobiles.in","r",stdin);
// freopen("mobiles.out","w",stdout);
n=m=read();
for(rr int i=1;i<=m;++i){
int u=read(),v=read();
if(u==-1)
++n,u=n,leaf[u]=true;
if(v==-1)
++n,v=n,leaf[v]=true;
son[i][0]=u,son[i][1]=v;
}
dfs(1,0);
for(rr int i=1;i<=n;++i){ // 深度差过大
if(leaf[i]&&abs(depth[i]-allmax)>1){
printf("-1"),exit(0);
}
}
solve(1,0);
printf("%d",ans);
return 0;
}
Day 1 T2
题意
给定 \(n\) 点 \(m\) 条边的无向图,点有点权 \(w_i\),边 \((u,v)\) 有边权 \(w_{u,v}\)。
你可以选择一些点。如果点 \(i\) 被选择,则其对答案贡献 \(w_i\)。
对于边 \((u,v)\):
- \(u\) 和 \(v\) 均被选择,对答案贡献 \(w_{u,v}\)
- \(u\) 和 \(v\) 选择了一个,对答案贡献 \(0\)
- \(u\) 和 \(v\) 均未被选择,对答案贡献 \(-w_{u,v}\)
求最大答案。
输入格式
第一行一个正整数 \(n\)。
接下来一行 \(n\) 个整数 \(w_1,w_2,...,w_n\)。
接下来一行一个正整数 \(m\)。
接下来 \(m\) 行,每行三个整数 \(u_i,v_i,w_{u_i,v_i}\),表示存在边 \((u_i,v_i)\),边权为 \(w_{u_i,v_i}\)。
输出格式
一行一个整数,表示最大答案。
对于 \(40\%\) 的数据,\(m=0\)。
对于另外 \(40\%\) 的数据,\(n,m \leq 20\)。
对于 \(100\%\) 的数据,\(1 \leq n,m \leq 10^5,1 \leq u_i,v_i \leq n,|w_i| \leq 10^9\)。
\(40\) 分
选取大于 \(0\) 的 \(w_i\)。
另外 \(40\) 分
\(O(2^n \times (n+m))\) 暴力枚举。
\(100\) 分
对于每条边,将边权加到两个端点的点权上,则答案为
即:所有大于 \(0\) 的点权之和减去边权之和。
注意此时 \(w_i\) 是被修改后的。
感性理解一下正确性。如果一条边两个端点都被选择,那么这条边权被多算了一次,需要减去。如果一条边选择了一个端点,那么这条边权不应该被加上,所以需要减掉。如果一条边两个端点都没选,根据题意,贡献为边权的相反值,所以也需要减掉。
所以 \(-(\sum w_{u,v})\) 不可避,我们只能想怎样让取到的点权最大。显然,取大于 \(0\) 的点权就行。
代码待补。
Day 1 T3
题意
在平面直角坐标系上有 \(n\) 个矩形,第 \(i\) 个矩形的左下角是 \((sx_i,sy_i)\),右上角是 \((tx_i,ty_i)\),且满足 \(sx_i,sy_i>0\)。
现在有 \(q\) 次询问,每次询问左下角为 \((0,0)\),右上角为 \((t,t)\) 的矩形与给出的 \(n\) 个矩形相交的面积。
输入格式
第一行两个正整数 \(n,q\)。
接下来 \(n\) 行,每行四个整数 \(sx_i,sy_i,tx_i,ty_i\)。
接下来 \(q\) 行,每行一个整数 \(t_i\),表示一次询问。
输出格式
对于每个询问,输出该矩形与给出的 \(n\) 个矩形相交的面积,重复的部分算多次。
对于 \(30\%\) 的数据,\(0 \leq t_i,sx_i,sy_i,tx_i,ty_i \leq 10^3\)。
对于 \(50\%\) 的数据,\(n \leq 10^3,q \leq 10^3\)。
另有 \(20\%\) 的数据,\(q=1\)。
对于 \(100\%\) 的数据,\(n \leq 5 \times 10^4,q \leq 10^5 ,0\leq t_i,sx_i,sy_i,tx_i,ty_i \leq 5 \times 10^6,sx_i<tx_i,sy_i<ty_i\)。
30 分
考虑对于每一个 \(1 \times 1\) 的小矩形,记录它被多少个矩形覆盖过。询问时暴力统计。\(O((n+q) \times tx_i \times ty_i)\)。
70 分
对于每次询问,遍历每一个矩形,用数学方法算出该询问中的正方形与每个矩形相交的面积。\(O(nq)\)。
100 分
考虑让每个矩形转换为四个左下角为 \((0,0)\) 的矩形的面积之和 / 差。
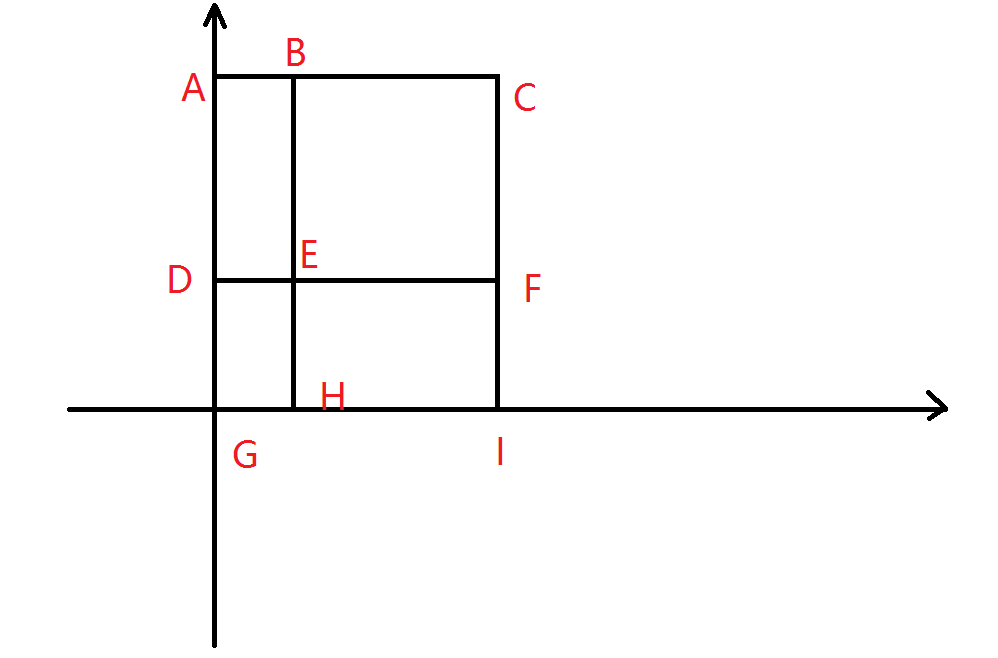
对于上图的矩形 \(BCEF\),其面积为 \(ACIG-ABHG-DFIG+DEHG\)。我们可以给每个矩形加上符号,例如 \(+ACIG,-ABHG,-DFIG,+DEHG\),这样可以在统计答案的时候知道该矩形对答案的贡献是正还是负。
转换后,每个矩形只需要记录右上角坐标 \((x,y)\) 即可,因为左下角坐标均为 \((0,0)\)。
对于一个右上角坐标为 \((x,y)\) 且符号为正的矩形,它和询问矩形的位置关系有四种情况:
- \(t < x,y\)
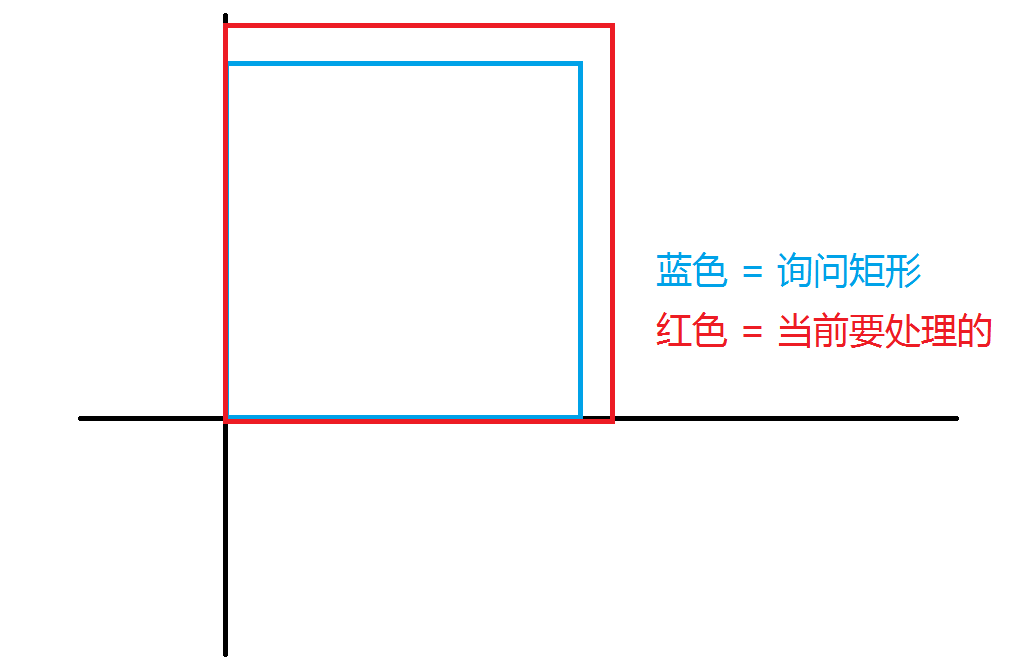
显然这种情况下询问矩形被当前矩形覆盖,贡献为 \(t^2\)。
- \(y \leq t, x > t\)
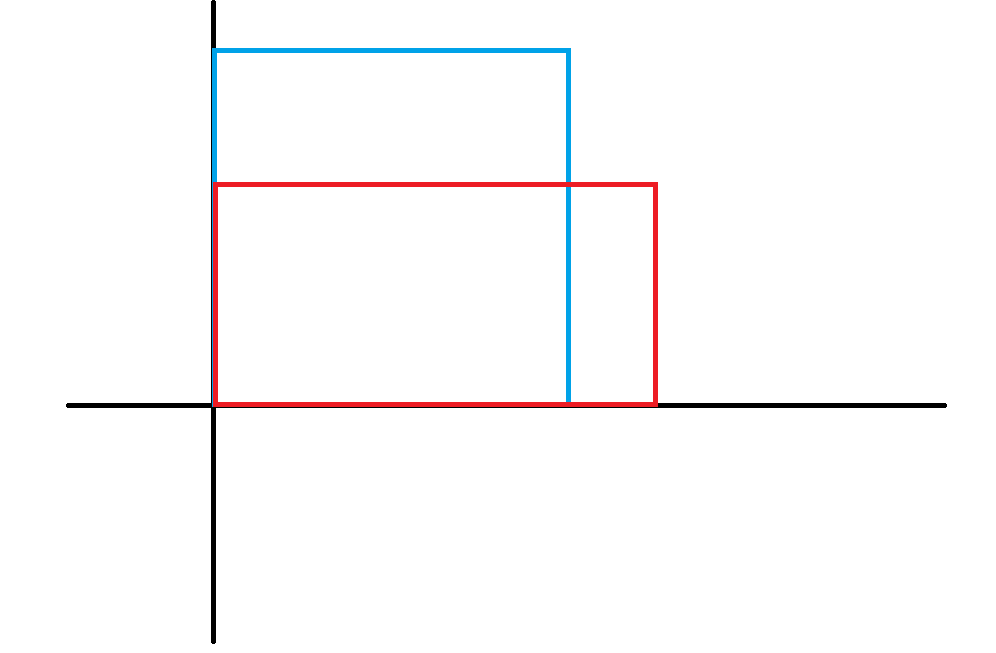
这种情况下,贡献为 \(y \times t\)。
- \(x \leq t,y > t\)
图与上一种情况类似,贡献为 \(x \times t\)。
- \(x,y \leq t\)
这种情况下询问矩形覆盖了当前矩形,贡献为 \(xy\)。
符号为负时,贡献取反即可。
第一种情况可以用一个变量 \(task_1\) 记录这样情况的矩形有多少个。根据乘法分配律,第二、三种情况可以用一个变量 \(task_2\) 记录这样情况的 \(x\) 与 \(y\) 的总和。第三种情况可以直接记录这种矩形的总面积。当然,如果符号为负,记录时符号仍然需要取反。
则一次询问的答案为
把一个矩形的 \(x,y\) 拆成两个独立的数,然后把 \(t_i\) 和 \(x,y\) 放在一起排序。最初,所有的矩形都是第一种情况。在遇到 \(t_i\) 时,根据当前的 \(task_{1,2,3}\) 计算出答案。在遇到 \(x\) 或 \(y\) 时,其对应的矩形情况发生了变化,将该矩形的贡献从原来的情况中减去,并加入到新的情况中。
时间复杂度 \(O((n+q)\log (n+q))\)。
# include <bits/stdc++.h>
# define rr
# define int long long
const int N=500010,INF=0x3f3f3f3f;
struct Node{
int val,id,v,ab;
/*
val 是横坐标 / 纵坐标
id 是矩阵编号 特殊地,如果当前为询问则 id = INF + 询问编号
v 是矩阵符号,1 or -1
ab = 0 为 x,ab = 1 为 y
*/
bool operator < (const Node &rhs) const{ // 询问放在最后处理
return val!=rhs.val?val<rhs.val:id<rhs.id;
}
}t[N*2];
int tot,cnt;
int n,q;
int ans[N];
int nowx[N],nowy[N];
bool del[N];
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-')f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
inline void add(int x,int y,int v,int id){
if(!x||!y){ // 矩形退化成线段或点的情况 没必要处理
return;
}
t[++tot].val=x,t[tot].id=id,t[tot].v=v,t[tot].ab=0;
t[++tot].val=y,t[tot].id=id,t[tot].v=v,t[tot].ab=1;
return;
}
signed main(void){
n=read(),q=read();
for(rr int i=1;i<=n;++i){
int sx=read(),sy=read(),tx=read(),ty=read();
add(tx,ty,1,++cnt);
add(sx,sy,1,++cnt);
add(sx,ty,-1,++cnt);
add(tx,sy,-1,++cnt); // 拆分
}
for(rr int i=1;i<=q;++i){
int x=read();
t[++tot].val=x,t[tot].id=INF+i,t[tot].v=0; // 询问
}
std::sort(t+1,t+1+tot);//放在一起排序
int task_1=0,task_2=0,task_3=0;
for(rr int i=1;i<=tot;++i){
task_1+=t[i].v;
}
task_1/=2; // 每个矩形被算了两次(x,y 各一次)
for(rr int i=1;i<=tot;++i){
if(t[i].id>INF){ // 询问
int trueid=t[i].id-INF,len=t[i].val; // 得到真实的询问编号
ans[trueid]=task_1*(len*len)+task_2*len+task_3;
continue;
}
if(t[i].ab==0){ // 记录 x/y 已经出现
nowx[t[i].id]=t[i].val;
}else{
nowy[t[i].id]=t[i].val;
}
if(nowx[t[i].id]&&nowy[t[i].id]){ // 第二种 / 第三种 -> 第四种
task_2-=(t[i].ab?(nowx[t[i].id]):(nowy[t[i].id]))*t[i].v,task_3+=nowx[t[i].id]*nowy[t[i].id]*t[i].v;
}else if(nowx[t[i].id]||nowy[t[i].id]){ // 第一种 -> 第二种 / 第三种
int suv=nowx[t[i].id]|nowy[t[i].id];
task_1-=t[i].v,task_2+=suv*t[i].v;
};
}
for(rr int i=1;i<=q;++i){
printf("%lld\n",ans[i]);
}
return 0;
}
Day 2 T1
题意
给定长为 \(n\) 的正整数数组 \(a_1,a_2,...,a_n\),每次操作可以选择区间 \([l,r]\),将 \(a_i(i \in [l,r])\) 减去 \(1\),求 \(a\) 均为 \(0\) 的最小操作次数,并输出方案。
输入格式
第一行一个正整数 \(n\),接下来一行 \(n\) 个正整数 \(a_1,a_2,...,a_n\)。
输出格式
第一行一个整数 \(m\),表示最小的操作次数。
接下来 \(m\) 行,每行两个正整数 \(l,r\),表示此次操作选择的区间为 \([l,r]\)。如果有多种方案,输出任意一种。
对于 \(10\%\) 的数据,\(n≤4,m≤10\)。
另有 \(20\%\) 的数据,\(n≤105,m≤20\)。
另有 \(30\%\) 的数据,\(n≤2000,m≤2000\)。
对于 \(100\%\) 的数据,\(1 \leq n≤105,0 \leq m≤10^5\)。
100 分
抛开方案,这是一道超级原题 —— 积木大赛,铺设道路。
对于输出方案,怎么办呢?
观察到,如果 \(a_i > a_{i-1}\),则需要增加 \(a_i - a_{i-1}\) 个 \(l=i\) 的操作,如果 \(a_i < a_{i-1}\),则有 \(a_{i-1} - a_i\) 个操作在 \(i-1\) 结束,即 \(r=i-1\)。
将可用的左端点存到队列里,每次 \(a_i > a_{i-1}\) 就往里面塞,否则就把里面的东西拿出来。如果处理完之后队列不为空,那剩下的操作右端点均为 \(n\)。
复杂度 \(O(n+m)\)。
# include <bits/stdc++.h>
# define rr
const int N=100010,INF=0x3f3f3f3f;
int n;
int a[N];
int now;
int ans;
int l[N],r[N],tot;
std::queue <int> nowl;
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-')f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
int main(void){
// freopen("range.in","r",stdin);
// freopen("range.out","w",stdout);
n=read();
for(rr int i=1;i<=n;i++){
a[i]=read();
if(now<a[i]){
ans+=(a[i]-now);
for(rr int j=1;j<=a[i]-now;++j){
nowl.push(i);
}
}else if(now>a[i]){
for(rr int j=1;j<=now-a[i];++j){
l[++tot]=nowl.front(),r[tot]=i-1,nowl.pop();
}
}
now=a[i];
}
for(rr int j=1;j<=a[n];++j){
l[++tot]=nowl.front(),r[tot]=n,nowl.pop();
}
printf("%d\n",ans);
for(rr int i=1;i<=tot;++i){
printf("%d %d\n",l[i],r[i]);
}
return 0;
}
Day 2 T2
题意
有 \(n\) 个点,权值分别为 \(a_1,a_2,...,a_n\)。你需要选择 \(m\) 个不相交的区间。第 \(i\) 个区间左右端点均在 \([1,n]\) 范围内,长必须为 \(D_i\),且该区间必须包含点 \(B_i\)。
求出被所选择区间包含的点权值之和的最大值。
对于 \(30\%\) 的数据,\(n≤100\);
对于 \(100\%\) 的数据,\(1≤n \leq 10^5\),\(1≤m≤n\),\(1≤a_i≤100\),\(D_i > 0,1 \leq B_i \leq n\)。\(B_i\) 和 \(D_i\) 保证,总存在合法的选择方案。
30 分
将需要选择的区间按照 \(B_i\) 排序,然后考虑 \(dp\)。设 \(dp_{i,j}\) 表示选择了 \(i\) 个区间,且最后一个区间的终点在 \(j\)。那么,当 \(B_i - D_i + 1 \leq j \leq B_i\) 时,
否则,\(dp_{i,j} = -\infty\)。
注意一下 \(i=1\) 的边界情况就行。
\(O(\sum D_i \times n)\)。
100 分
可以将所有的 \(dp_{i-1,j}\) 扔进线段树里,做到 \(O(\log n)\) 转移。因为转移只和 \(i-1\) 有关,所以不用开二维数组了。
总复杂度 \(O(\sum D_i \log n)\),因为保证有解,所以即 \(O(n \log n)\)。
# include <bits/stdc++.h>
# define rr
const int N=100010,INF=0x3f3f3f3f;
struct Node{
int b,len;
bool operator < (const Node &rhs) const{
return b<rhs.b;
}
}a[N];
int val[N],sum[N];
int dp[N];
int n,m;
int maxx[N<<2];
inline int read(void){
int res,f=1;
char c;
while((c=getchar())<'0'||c>'9')
if(c=='-')f=-1;
res=c-48;
while((c=getchar())>='0'&&c<='9')
res=res*10+c-48;
return res*f;
}
inline int lc(int x){
return x<<1;
}
inline int rc(int x){
return x<<1|1;
}
int lrange(int x){
return std::max(x,1);
}
int rrange(int x){
return std::min(x,n);
}
int presum(int l,int r){
return sum[r]-sum[l-1];
}
void change(int k,int l,int r,int x,int v){
if(l==r){
maxx[k]=v;
return;
}
int mid=(l+r)>>1;
if(x<=mid)
change(lc(k),l,mid,x,v);
else
change(rc(k),mid+1,r,x,v);
maxx[k]=std::max(maxx[lc(k)],maxx[rc(k)]);
}
int ask(int k,int l,int r,int L,int R){
if(L<=l&&r<=R){
return maxx[k];
}
int mid=(l+r)>>1,res=-INF;
if(L<=mid)
res=std::max(res,ask(lc(k),l,mid,L,R));
if(mid<R)
res=std::max(res,ask(rc(k),mid+1,r,L,R));
return res;
}
int main(void){
// freopen("fish.in","r",stdin);
// freopen("fish.out","w",stdout);
memset(dp,0xcf,sizeof(dp));
n=read();
for(rr int i=1;i<=n;++i){
val[i]=read();
sum[i]=sum[i-1]+val[i];
}
m=read();
for(rr int i=1;i<=m;++i){
a[i].b=read(),a[i].len=read();
}
std::sort(a+1,a+1+m);
int lstl=std::max(a[1].b,a[1].len),lstr=rrange(a[1].b+a[1].len-1);
for(rr int i=std::max(a[1].b,a[1].len);i<=rrange(a[1].b+a[1].len-1);++i){
dp[i]=presum(i-a[1].len+1,i);
change(1,1,n,i,dp[i]);
}
for(rr int i=2;i<=m;++i){
for(rr int j=std::max(a[i].b,a[i].len);j<=rrange(a[i].b+a[i].len-1);++j){
int l=lstl,r=j-a[i].len;
if(l>r){
continue;
}
dp[j]=ask(1,1,n,l,r)+presum(j-a[i].len+1,j);
}
lstl=std::max(a[i].b,a[i].len),lstr=rrange(a[i].b+a[i].len-1);
for(rr int j=std::max(a[i].b,a[i].len);j<=rrange(a[i].b+a[i].len-1);++j){
change(1,1,n,j,dp[j]);
}
}
int ans=-INF;
for(rr int i=1;i<=n;++i){
ans=std::max(ans,dp[i]);
}
printf("%d",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号