开关函数分析
开关函数分析法是线性时变状态的一种特殊情况,它要求一个信号足够大,另一个信号足够小。
单二极管调幅电路
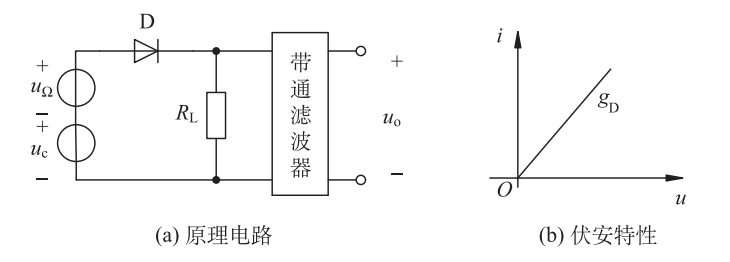
输入信号和控制信号相加后作用在二极管上
若二极管的伏安特性可以近似为直线,且导通区折线的斜率为
当,且时,
式中,为二极管导通区的折线斜率;为二极管交流电阻。
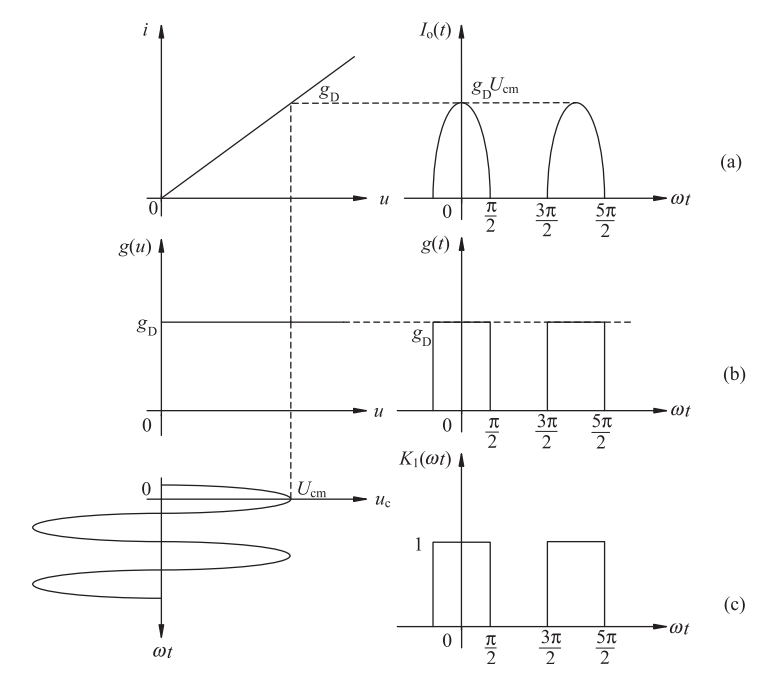
在 的负半周(当 时),二极管截止,流过负载 的电流为 。
故在的整个周期内,流过负载的电流可以表示为
现引入开关函数
该函数表示高度为 1 的单向周期性方波,称为单向开
关函数,于是电流 i 可以表示为
单向开关函数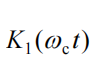 的傅里叶级数展开式为
的傅里叶级数展开式为
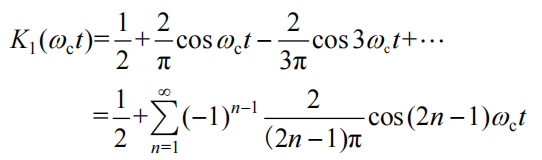
代入电流表达式中,可得电流 i 中包含的频率分量为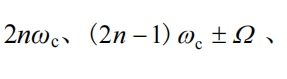
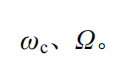

通过设计带宽 的带通滤波器,取出通频带内的频率分量,可以产生调幅信号。电路可以实现频谱搬移功能。


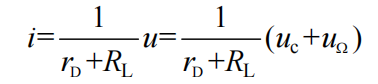
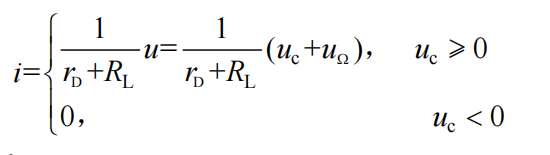
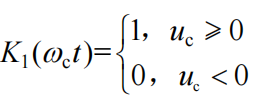
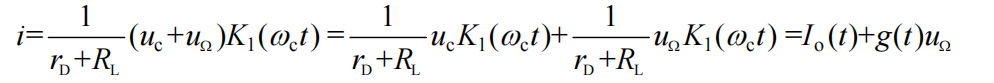


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 使用C#创建一个MCP客户端
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现