仿射密码

仿射密码是一种替换密码，利用加密函数一个字母对一个字母的加密。

加密函数：E(x) = (ax + b) (mod m)，其中

• a和m互质
• m是字母的数量

解密函数：D(x) = a^-1(x - b) (mod m)，其中a^-1是a在Z_m群的乘法逆元。

仿射密码 为单表加密的一种，字母系统中所有字母都藉一简单数学方程加密，对应至数值，或转回字母。 其仍有所有替代密码之弱处。所有字母皆借由方程E(x) = (ax + b) (mod m)加密，b 为移动大小。

 

加密与解密

加密

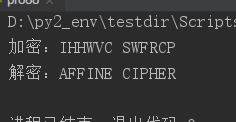
以加密函数E(x) = (5x + 8) (mod 26)为例，以字母表26个字母作为编码系统

 

明文	A	F	F	I	N	E	C	I	P	H	E	R
x	0	5	5	8	13	4	2	8	15	7	4	17
$\mathrm{y = 5x+8}$	8	33	33	48	73	28	18	48	83	43	28	93
$\mathrm{y mod 26}$	8	7	7	22	21	2	18	22	5	17	2	15
密文	I	H	H	W	V	C	S	W	F	R	C	P

对应的加密结果为：IHHWVCSWFRCP

解密

在已知a = 5，m = 26的情况下，我们需要求a关于模m的逆元，得到a^-1 = 21

因此解密函数为：D(x) = 21(x - 8) (mod 26)

 

密文	I	H	H	W	V	C	S	W	F	R	C	P
$y$	8	7	7	22	21	2	18	22	5	17	2	15
$\mathrm{x = 21(y-8)}$	0	-21	-21	294	273	-126	210	294	-63	189	-126	147
$\mathrm{x mod 26}$	0	5	5	8	13	4	2	8	15	7	4	17
明文	A	F	F	I	N	E	C	I	P	H	E	R

 

 

脚本

使用字母表加密解密的脚本：

# -*- coding:utf-8 -*-

import string

letters = string.ascii_letters

def encode(plaintext, a, b):
    encode_str = ''
    for s in plaintext:
        if s in letters:
            n = letters.find(s) % 26
            y = (a * n + b) % 26
            if s.isupper():
                y = y + 26
            encode_str += letters[y]
        else:
            encode_str += s
    return encode_str

def ext_euclid(a, m):
    if m == 0:
        return 1, 0
    else:
        x, y = ext_euclid(m, a % m)
        x, y = y, (x - (a // m) * y)
        return x,y

def decode(encodes, a, b):
    decode_str = ''
    x = ext_euclid(a,26)
    a = x[0]
    if a < 0:
        a = a + 26
    for s in encodes:
        if s in letters:
            n = letters.find(s) % 26
            y = a * (n - b) % 26
            if s.isupper():
                y += 26
            decode_str += letters[y]
        else:
            decode_str += s
    return decode_str

if __name__ == '__main__':
    plaintext = 'AFFINE CIPHER'
    a = 5
    b = 8
    s = encode(plaintext,a,b)
    print ("加密："+ s)
    d = decode(s, a, b)
    print ("解密：" + d)

 

 

破解

首先，我们可以看到的是，仿射密码对于任意两个不同的字母，其最后得到的密文必然不一样，所以其也具有最通用的特点。当密文长度足够长时，我们可以使用频率分析的方法来解决。

其次，我们可以考虑如何攻击该密码。可以看出当$\mathrm{a=1时，仿射加密是凯撒加密。而一般来说，我们利用仿射密码时，其字符集都用的是字母表，一般只有\; 26\; 个字母，而不大于\; 26\; 的与\; 26\; 互素(1,3,5,7,9,11,15,17,19,21,23,25)的个数一共有}$

 Φ(26) = Φ(2) x Φ(13) = 12

算上b的偏移可能，一共有可能的密钥空间大小也就是

12 x 26 = 312

一般来说，对于该种密码，我们至少得是在已知部分明文的情况下才可以攻击。下面进行简单的分析。

这种密码由两种参数来控制，如果我们知道其中任意一个参数，那我们便可以很容易地快速枚举另外一个参数得到答案。

但是，假设我们已经知道采用的字母集，这里假设为 26 个字母，我们还有另外一种解密方式，我们只需要知道两个加密后的字母 ${\mathrm{y1,y2即可进行解密。那么我们还可以知道}}^{}$

y₁ = (ax₁ + b) (mod 26)

y₂ = (ax₂ + b) (mod 26)

两式相减得

y₁ - y₂ = a(x₁ - x₂) (mod 26)

这里 ${\mathrm{y1,y2已知，如果我们知道密文对应的两个不一样的字符 x1与x2 ，那么我们就可以很容易得到 a ，进而就可以得到b 了。}}^{}$

 

${\mathrm{例子}}^{}$

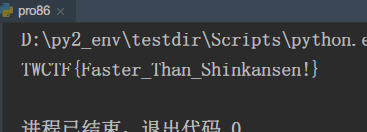
${\mathrm{TWCTF\; 2016的super\_express}}^{}$

import sys
key = '****CENSORED***************'
flag = 'TWCTF{*******CENSORED********}'

if len(key) % 2 == 1:
    print("Key Length Error")
    sys.exit(1)

n = len(key) / 2
encrypted = ''
for c in flag:
    c = ord(c)
    for a, b in zip(key[0:n], key[n:2*n]):
        c = (ord(a) * c + ord(b)) % 251
    encrypted += '%02x' % c

print encrypted

加密得到：805eed80cbbccb94c36413275780ec94a857dfec8da8ca94a8c313a8ccf9

对于 flag 中的每个字母都加密了 n 次，仔细分析，我们可以发现

　　　　　　　　c₁ = a₁c + b₁

　　　　　　　　c₂ = a₂c₁ + b₂

　 　　　　　　　　= a₁a₂c + a₂b₁ + b₂

　 　　　　　　　　= kc + d

根据第二行的推导，我们可以得到其实 ${\mathrm{cn 也是这样的形式，可以看成 cn=xc+y ，并且，我们可以知道的是，key\; 是始终不变化的，所以说，其实这个就是仿射密码。}}^{}$

此外，题目中还给出了密文以及部分部分密文对应的明文，那么我们就很容易利用已知明文攻击的方法来攻击了，利用代码如下

# -*- coding:utf-8 -*-

import gmpy

key = '****CENSORED***************'
flag = 'TWCTF{*******CENSORED********}'

data = "805eed80cbbccb94c36413275780ec94a857dfec8da8ca94a8c313a8ccf9"
encrypted = [int(data[i:i + 2], 16) for i in range(0, len(data), 2)]
plaindelta = ord(flag[1]) - ord(flag[0])
cipherdalte = encrypted[1] - encrypted[0]
a = gmpy.invert(plaindelta, 251) * cipherdalte % 251
b = (encrypted[0] - a * ord(flag[0])) % 251
a_inv = gmpy.invert(a, 251)
result = ""
for c in encrypted:
    result += chr((c - b) * a_inv % 251)
print result

gmpy安装方式：点击进入

 

在线加密解密网站：https://crypto.interactive-maths.com/affine-cipher.html

 

参考

https://zh.wikipedia.org/wiki/%E4%BB%BF%E5%B0%84%E5%AF%86%E7%A2%BC

https://en.wikipedia.org/wiki/Affine_cipher

https://ctf-wiki.github.io/ctf-wiki/crypto/classical/monoalphabetic-zh/