第十届蓝桥杯(含题目文件下载)

A组C/C++下载链接：https://www.lanzous.com/i3jmx4b

B组C/C++下载链接：https://www.lanzous.com/i3jf1qj

B组JAVA下载链接：https://www.lanzous.com/i3jmxli

据官方消息：软件类这周三会尽量出成绩，最迟星期四。

第一二题，基本nc题，代码其实都不需要了。（我的答案仅供参考，毕竟一周后才出结果。祝愿各位都能有个好的成绩！！！）

A题组队

490

B题年号字串

BYQ

C题数列求值

【问题描述】
给定数列1，1，1，3，5，9，17，..，从第4项开始，每项都是前3项的和。求第20190324项的最后4位数字。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。

本题的结果为一个4位整数（提示：答案的千位不为0），在提交答案时只填写这个整数，填写多余的内容将无法得分。

#include <bits/stdc++.h>

#define N 20190324
using namespace std;

static int x = []() {std::ios::sync_with_stdio(false); cin.tie(0); return 0; }();

int main()
{
    vector<int> vec(N, 1);

    for (int i = 3; i < vec.size(); ++i) {
        vec[i] = vec[i - 1] + vec[i - 2] + vec[i - 3];
        if (vec[i] > 9999) {
            vec[i] = vec[i] - (vec[i] / 10000) * 10000;//只保留后四位，那我们就以10000为1个单位进行减法，直到小于10000。
        }
    }
    cout << vec[vec.size() - 1];

    return 0;
}

答案：4659

D题数的分解

【问题描述】

把2019分解成3个各不相同的正整数之和，并且要求每个正整数都不包含数字2和4，一共有多少种不同的分解方法？.
注意交换3个整数的顺序被视为同一种方法，例如1000-1001-18和1001+1000+18 被视同一种。

哎，这是一个正整数，得从1开始，并且要想不重复，那么i,j,k三个数之间要有 i , j = i + 1, k = j + 1

 #include <bits/stdc++.h>

using namespace std;bool func(int n) {
    bool flag = true;
    while (1) {
        if (n < 10) {
            if (n == 2 || n == 4) {
                flag = false;
                break;
            }
            break;
        }
        int m = n % 10;
        n = n / 10;
        if (m == 2 || m == 4) {
            flag = false;
            break;
        }
    }

    return flag;
}

int main()
{
    int ncount = 0;
    for (int i = 1; i < 2019; ++i) {
        for (int j = i + 1; j < 2019; ++j) {
            for (int k = j + 1; k < 2019; ++k) {
                if (func(i) && func(j) && func(k) && i + k + j == 2019) {
                    ncount++;
                }
            }
        }
    }

    cout << ncount << endl;

    return 0;
}

答案：40785

E题迷宫

【问题描述】
下图给出了一个迷宫的平面图，其中标记为 1 的为障碍，标记为 0 的为可以通行的地方。

010000
000100
001001
110000

迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这个它的上、下、左、右四个方向之一。
对于上面的迷宫，从入口开始，可以按DRRURRDDDR 的顺序通过迷宫，一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。
对于下面这个更复杂的迷宫（30 行 50 列），请找出一种通过迷宫的方式，其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。请注意在字典序中D<L<R<U。（如果你把以下文字复制到文本文件中，
请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 maze.txt，内容与下面的文本相同）

01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个字符串，包含四种字母 D、U、L、R，在提交答案时只填写这个字符串，填写多余的内容将无法得分。

#include <bits/stdc++.h>

using namespace std;

#define N 50
#define M 30


int visited[M][N] = { 0 };//记忆已经经过的点（0表示未经过，1表示经过）
int Move[4][2] = { {1,0},{0,-1},{0,1},{-1,0} };//用来移动点
char direction[4] = { 'D','L','R','U' };//与上面的二维数组的第一维索引号对应
struct Point {
    int x;//横坐标
    int y;//纵坐标
    string str;//记忆点的轨迹
    int step;//经过距离
    Point(int xx, int yy, int ss, string s) {//构造函数
        x = xx;
        y = yy;
        str = s;
        step = ss;
    }
};

int MAP[M][N]{//迷宫
{0,1,0,1,0,1,0,1,0,0,1,0,1,1,0,0,1,0,0,1,0,1,0,1,1,0,0,1,0,1,1,0,1,0,0,1,0,0,0,0,1,0,0,0,1,0,1,0,1,0},
{0,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,1,1,0,0,1,1,0,1,0,0,1,0,1},
{0,1,1,1,1,0,1,1,0,1,0,0,1,0,0,0,1,0,0,0,0,0,1,1,0,1,0,0,1,0,1,1,1,0,0,0,1,1,0,0,0,0,0,0,0,1,0,0,0,0},
{0,1,0,0,0,0,0,0,0,0,1,0,1,0,1,0,0,0,1,1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,1,0,1,0,1,0,1,0,1,1,0,0,1,0,1,1},
{0,0,0,1,1,1,1,1,0,0,0,0,0,0,1,0,1,0,0,0,0,1,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,1,0,1,1,0,0,0,0,0,0,0,0},
{1,1,0,0,1,0,0,0,1,1,0,1,0,1,0,0,0,0,1,0,1,0,1,1,0,0,0,1,1,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,1,0,1,1,1},
{0,0,0,1,1,0,1,1,0,1,0,1,0,1,0,0,1,0,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,1,0,1,0,0,1,1,1,0,0,0,0,0,0,0},
{1,0,1,0,0,0,0,0,1,0,1,0,0,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,1,1,0,0,1,1,0,0,0,0,1,0,0,0,0,1,1,1,0,1,0},
{0,0,1,1,1,0,0,0,0,0,1,0,1,0,1,0,0,0,0,1,1,0,0,0,1,0,0,0,0,0,0,1,0,0,0,1,0,1,0,0,1,1,0,0,0,0,1,0,0,1},
{1,1,0,0,0,1,1,0,1,0,0,0,0,1,1,1,0,0,1,0,0,0,1,0,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,0,0,1,1,0,1,0,0,0},
{0,0,0,1,0,0,0,0,1,0,0,1,0,0,0,0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,1,0,1,0,0,0,1,0,1,0,1,0,1,0,0,0,0,1,0,1},
{1,1,1,0,0,1,0,0,1,0,1,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,1,0,1,0,1,0,1,0,1,0,0,1,0,0,1,0,0,0,1,0,1,0,0},
{0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,1,1,0,0,1,1,1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,0,1,0,1,0,1,0,0,0,1,1},
{1,0,1,0,1,0,1,0,0,1,1,1,0,0,0,0,1,0,0,0,0,1,1,0,0,0,0,1,0,1,1,0,0,1,1,1,1,0,1,1,0,1,0,0,0,0,1,0,0,0},
{1,0,1,0,1,0,1,0,1,0,0,0,0,1,1,0,1,0,1,0,1,0,0,1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,1,1,1,0,1,1,1,0,1,0,0,1},
{1,0,0,0,0,0,0,0,1,0,1,1,0,0,0,1,0,0,0,0,1,0,1,1,0,0,1,0,1,1,0,1,0,0,1,0,1,1,1,0,0,0,0,0,0,0,0,1,0,0},
{1,0,1,0,1,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,1,1,1,1,0,1,0,1,0,0,1},
{0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,0,1,0,0,1,0,1,0,1,0,0,0,1,1,0,1,0,1,0,1,1,0,1,1,1,0,0,0,0,1,1,0,1,0,1},
{1,1,0,0,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,0,0,0,1,0,0,0,1,1,1,0,0,0,0,1,0},
{0,0,0,0,1,0,0,0,1,1,0,0,0,0,1,1,0,1,0,1,1,0,1,0,0,0,0,0,0,1,0,0,1,0,1,0,0,1,0,0,1,0,0,0,0,1,1,1,0,1},
{1,0,1,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,1,1,1,0,1,1,0,0,1,0,1,1,0,1,0,1,1,0,1,0,1,0,1,0,0,0,0,1},
{0,0,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,1,0,1,0,1,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,1,0,0,0,1,0,0,0,1,0,1,0,1},
{1,0,1,0,0,0,0,1,0,0,0,1,1,0,0,1,0,0,0,1,0,0,0,0,1,0,1,0,1,0,0,1,0,1,0,1,0,1,0,1,1,1,1,1,0,1,0,0,1,0},
{0,0,0,0,0,1,0,0,1,0,1,0,0,0,0,0,0,1,1,0,0,1,0,1,0,0,1,0,1,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,1,0},
{1,1,0,1,0,0,0,0,0,0,1,0,0,1,1,1,0,1,1,1,0,0,1,0,0,1,0,0,0,0,1,1,1,0,1,0,0,1,0,1,1,0,1,1,1,0,1,0,0,0},
{0,0,0,0,0,1,1,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,1,1,1,0,1,0,0,0,0,0,0,1,1,0,0,1,1},
{1,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,1,0,0,0,1,1,1,1,1,0,0,0,1,0,1,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0},
{1,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,1,0,1,0,1,1,0,0,0,0,0,0,0,1,0,0,1,0,1,0,1,0,0,0,1,0,1,1,1,0,1,0,0,0},
{0,0,1,1,1,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,1,1,0,1,1,1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,1,1},
{1,0,0,0,0,0,0,1,1,0,0,1,1,1,0,1,0,1,1,1,0,1,0,0,0,1,0,0,0,1,1,0,1,1,1,0,1,0,1,0,1,1,0,1,1,1,1,0,0,0}
};

bool check(int x, int y) {//检查是否越界/走重复点/遇到墙
if (x < 0 || x >= M || y < 0 || y >= N || visited[x][y] || MAP[x][y] == 1)
    return false;
return true;
}

void BFS() {
    queue<Point> q;
    Point p(0, 0, 0, "");//初始化队列，从0,0点出发
    q.push(p);
    visited[0][0] = 1;
    //下面代码的整体思路：将我们现在到达的点P周围，可行点存入队列中，选择其中一个点作为点P更新，再将旧的P点从队列中删除，再以这个点重复之前找点的操作。
    //当这条路为死路时，会回到队列中另一个可行点，再次搜索，直到找到目标点。
    while (!q.empty()) {
        Point fro = q.front();//取出队头
        if (fro.x == M - 1 && fro.y == N - 1) {//当到达右下角时，输出路径信息与步数，退出
            cout << fro.str << endl;
            cout << fro.step << endl;
            break;
        }
        q.pop();
        for (int i = 0; i < 4; ++i) {
            int nx = fro.x + Move[i][0];
            int ny = fro.y + Move[i][1];
            if (check(nx, ny)) {
                q.push(Point(nx, ny, fro.step + 1, fro.str + direction[i]));
                visited[nx][ny] = 1;
            }
        }
    }
}

int main() {
    BFS();
    return 0;
}

答案：DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR

F题特别数的和

小明对数位中含有 2、0、1、9 的数字很感兴趣（不包括前导0），在1 到 40 中这样的数包括1、2、9、10 至 32、39 和 40，共 28 个，他们的和是 574。请问，在 1 到n 中，所有这样的数的和是多少？

【输入格式】
输入一行包含两个整数n。

【输出格式】
输出一行，包含一个整数，表示满足条件的数的和。

【样例输入】

40

【样例输出】

574

【评测用例规模与约定】
对于20% 的评测用例，1≤n≤10
对于50% 的评测用例，1≤n≤100
对于80% 的评测用例，1≤n≤1000
对于所有评测用例，1≤n≤10000

#include <bits/stdc++.h>

using namespace std;

bool check(int n) {
    int flag = false;
    while (1) {
        if (n < 10) {
            if (n == 2 || n == 1 || n == 9 || n == 0) {
                flag = true;
            }
            break;
        }
        int k = n % 10;
        if (k == 2 || k == 1 || k == 9 || k == 0) {
            flag = true;
        }
        n /= 10;
    }
    return flag;
}

int main()
{
    int num, sum = 0;
    cin >> num;
    for (int i = 1; i <= num; ++i) {
        if (check(i)) {
            sum += i;
        }
    }

    cout << sum;
    return 0;
}

G题完全二叉树的权值

给定一棵包含N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是A1,A2,...,AN ，如下图所示：

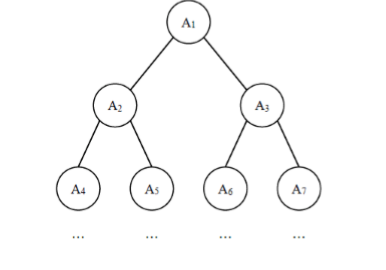
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。
注：根的深度是1。

【输入格式】
第一行包含一个整数N。
第二行包含N 个整数A1,A2,...,AN

【输出格式】
输出一个整数代表答案。

【样例输入】

7
1 6 5 4 3 2 1

【样例输出】

2

【评测用例规模与约定】
对于所有评测用例，1≤N≤100000 ，−100000≤Ai≤100000 。

这道题，需要注意的地方是可以为负值，难度都不大，每个二叉树每层最多2^(n-1)个,所以，实际上就是比较第sum(1, 2^0),sum(2^0+1,2^1),sum(2^1+1,2^2)....中取max的深度n。

我写的这个复杂了，可以自己试试简化。

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int n, sum = 0, maxnum = 0, d = 1;
    cin >> n;
    vector<int> vec(n);
    for (int i = 0; i < n; ++i) {
        cin >> vec[i];
    }
    maxnum = vec[0];
    if (n == 1) {
        cout << d << endl;
        return 0;
    }
    vec.erase(vec.begin());
    for (int i = 1; pow(2, i) <= vec.size(); ++i) {
        sum = accumulate(vec.begin(), vec.begin() + pow(2, i), 0);
        //cout << sum << endl;
        //cout << sum << " " << maxnum << endl;
        if (sum > maxnum) {
            maxnum = sum;
            d = i + 1;
        }
        vec.erase(vec.begin(), vec.begin() + pow(2, i));
    }
    if (!vec.empty()) {
        sum = accumulate(vec.begin(), vec.end(), 0);
        if (sum > maxnum) {
            d = d + 1;
        }
    }
    cout << d;
    return 0;
}

H题等差数列

数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列，只记得其中N 个整数。
现在给出这N 个整数，小明想知道包含这N 个整数的最短的等差数列有几项？
【输入格式】
输入的第一行包含一个整数N。
第二行包含N 个整数A1,A2,...,AN (注意：A1~AN并不一定是按等差数列中的顺序给出)

【输出格式】
输出一个整数表示答案。

【样例输入】

5
2 6 4 10 20

【样例输出】

10

【样例说明】
包含2、6、4、10、20 的最短的等差数列是2、4、6、8、10、12、14、16、18、20。

【评测用例规模与约定】
对于所有评测用例，2≤N≤100000 ，0≤Ai≤10^9

解决办法是：排列数列之后，找出两两之间的差值最小值作为公差。这道难度不大，但是有坑在，常数列的数目是n ，所以要单独讨论常数列。

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int n, count;
    cin >> n;
    vector<int> vec(n), vec1(n - 1);
    for (int i = 0; i < n; ++i) {
        cin >> vec[i];
    }
    sort(vec.begin(), vec.end());//数列排序
    if (accumulate(vec.begin(), vec.end(), 0) == n * vec[0]) {//当为常数列时，等差项有n项(前n项和==n*vec[0])
        cout << n;
        return 0;
    }

    for (int i = 0; i < n - 1; ++i) {
        vec1[i] = vec[i + 1] - vec[i];
    }
    sort(vec1.begin(), vec1.end());//数列之间从差，排序
    count = (vec.back() - vec.front()) / (*vec.begin()) + 1;
    cout << count;

    return 0;
}

有N个“+”，M个“-”， N+M+1个整数

凉凉，坑啊！还以为25分这么好得，暴力解决，这道等结果吧，也不确定自己对没有。

24个正号，1个负号，-25~-1 和 1这就26个整数，可以这样计算1-(-1+(-2)+(-3)...+(-25))，要考虑括号。

测试用例：

2 1
1 -20 30 -100

答案是151，过程：

1+30-(-20+(-100))

最后一道，我选择战略性放弃。

posted @ 2019-03-24 17:04 Hk_Mayfly 阅读(1858) 评论(0) 编辑收藏举报

刷新页面返回顶部

Hk_Mayfly

凡心所向，素履以往。生如逆旅，一苇以航。

第十届蓝桥杯(含题目文件下载)

A题组队

B题年号字串

C题数列求值

D题数的分解

E题迷宫

F题特别数的和

G题完全二叉树的权值

H题等差数列

公告

Hk_Mayfly

凡心所向，素履以往。生如逆旅，一苇以航。

第十届蓝桥杯(含题目文件下载)

A题 组队

B题 年号字串

C题 数列求值

D题 数的分解

E题 迷宫

F题 特别数的和

G题 完全二叉树的权值

H题 等差数列

公告

A题组队

B题年号字串

C题数列求值

D题数的分解

E题迷宫

F题特别数的和

G题完全二叉树的权值

H题等差数列