2019美国大学生数学建模竞赛B题（思路）
建模比赛已经过去三天了，但留校的十多天里，自己的收获与感受依然长存于心。下面的大致流程，很多并没有细化，下面很多情况都是在假设下进行的，比如假设飞机能够来回运送药品，运货无人机就只运货，在最大视距下侦查等。
题目下载：点击下载
首先，因为这道题中的变量太多，我们需要对变量的数量进行减小。
一.变量设置
二.约束条件
1.从基地运输到医院的药包量必须满足医院的需求。
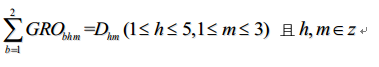
2.无人机最大行驶距离能否满足来回医院。
三.目标函数
1.计算基地到医院的时间：
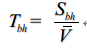
2.我们希望时间最优（最短），则取满足约束条件b的无人机运送航线的时间最大值，使得时间花费最长的取最小值，则总时间最短。
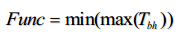
通过上面流程，我们通过程序计算，能够把需求量，运送花费时间，基地位置（经纬度）等都能够算出来。这是两个基地的情况，我们能够再增加一个基地，得出一个时间。将它与两个基地进行比较，看哪一个更短。这样一来，我们剩下的问题就是解决，派什么类型的飞机运送了。
四.通过上面，我们得出了3个基地应该是最优的情况。
我们将救援过程分为两个过程：
- 运送急救包
- 侦查路段
1.第一阶段：
a.通过医院对各种药物的需求量和医院到基地的距离，建立函数和约束条件，选择无人机的类型。
2.第二阶段：
a.计算无人机扫描的圆半径
在这里我们考虑了海拔高度。
b.建立函数，使得函数满足无人机能够满足来回侦查圆的最远位置，约束条件，在这情况下速度要尽肯能快，选出飞机类型。
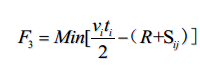
为了计算运输药物实际需要的无人机的数量，存在每架无人机每天最多出任务次数与实际需要的无人机数量的乘积为理论上需要的无人机数量。以此我们能够列出函数式。
c.我们以医院为中心，5公里为半径圆的范围内侦查。我们将侦查情况分为两种：
- 在基地在侦查圆内
- 基地在侦查圆外
基地在圆内
1.我们需要求无人机飞行的总路径，我们将它分为圆内路径长度和弧长。
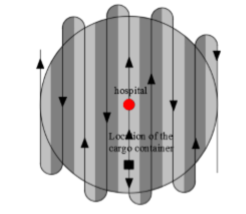
a.我们能够将圆内的每个小块看成梯形或者矩形，微元法计算。
建立等式，梯形/矩形总面积等于侦查圆的总面积。从而，我们可以得到圆内部分的总路径长度。
b.将圆外的转弯弧看成圆弧，无人机扫描的半径实际就是它的半径，长度也就很好算出了。至于转弯弧总的个数，我通过观察得到
这样，我们通过总路径，得到需要的飞机数量。
基地在圆外
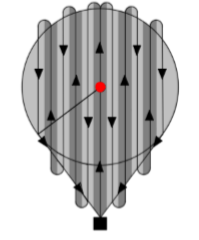
实际上，这里的总方法也是一样的，变的是总路径和侦查的面积，阴影部分是扫描的面积，总路径长度，依然是阴影部分内部长度加上转弯弧长度，不过这里还需要多出两条切线的长度。
同样的，这里我们也可以算出飞机需求的数量。
五.装箱问题(背包问题)
将无人机箱，药包箱，运货箱三种装入到集装箱中的问题，类似于三维装箱问题，不过这里需要考虑，运货箱放在无人机箱还是集装箱中。
这里进行模型的模拟，可以使用loadexpert或者loadmaster软件模拟。
这里的算法可以借鉴：
文章下载：点击进入
有想参加数学建模的，或者正在参加的朋友，欢迎加我QQ，关注我，大家一起讨论交流，一起奋斗。
