演员-评论员法(Actor-Critic)

演员-评论员算法( Actor-Critic Algorithm)是一种结合策略梯度和时序差分学习的强化学习方法。其中演员(Actor)是指策略函数 \(\pi _\theta\left( {a|s} \right)\)，即学习一个策略来得到尽量高的回报。评论员(Critic)是指值函数 \({V_\phi }\left( {{s_t}} \right)\)，对当前策略的值函数进行估计，即评估演员的好坏。

1 REINFORCE 改进

在 REINFORCE 算法中每次需要用一个策略采集完一条完整的轨迹，并计算这条轨迹上的回报。这个方法有两个缺点：

1. 方差比较大
2. 学习效率低

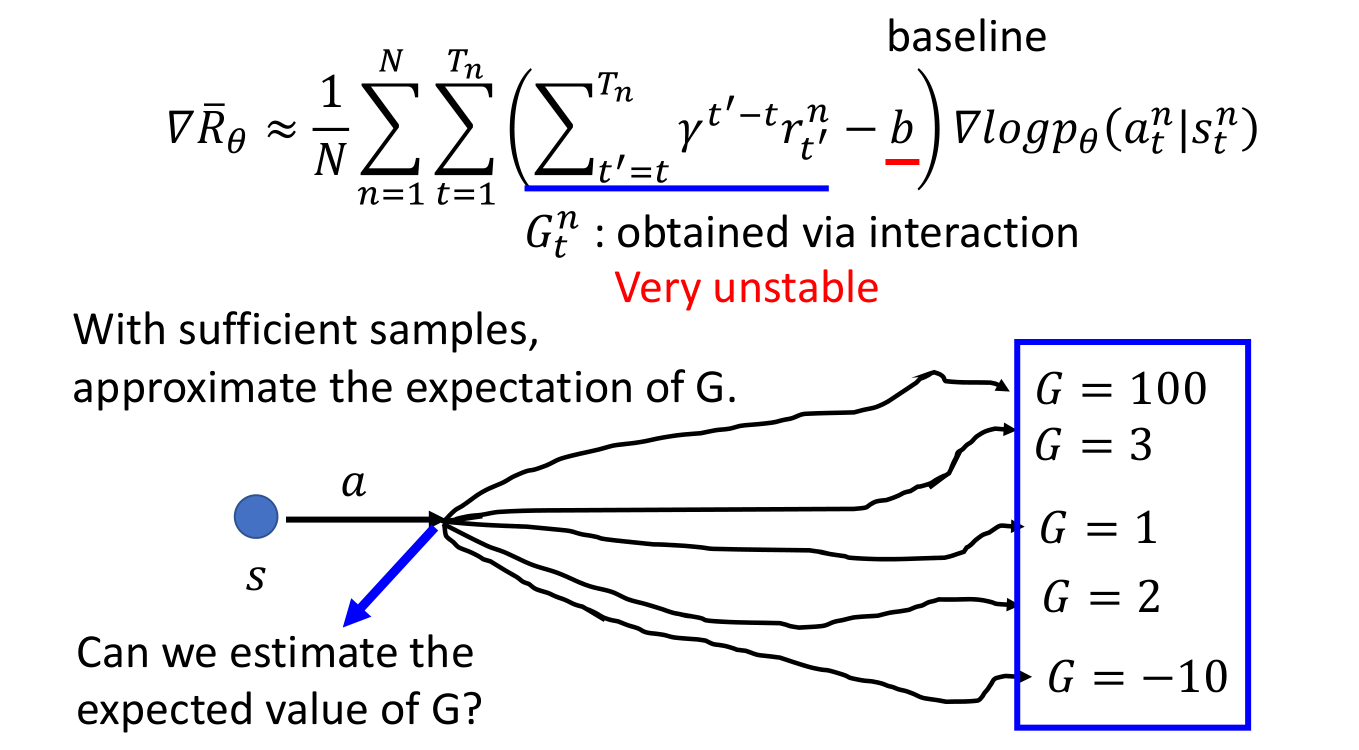
学习效率低很好理解，为什么说方差大呢？下面是李宏毅的课件中的图，因为我们在去评估在状态 \(s_t\) 时采取动作 \(a_t\) 的好坏时，需要用到这个总回报 \(G\)，最准确的做法当时是对这个 \(G\) 求期望了，然后在实际操作的时候其实是只用了一次采样来代替这个期望了。从下图中也可以看出来，这个回报 \(G\) 的随机性还是挺大的。

Return

解决这个问题的做法是可以借助时序差分学习的思想，即从状态 \(s\) 开始的总回报可以通过当前动作的即时奖励 \(r(s,a,s^{\prime})\) 和下一个状态 \(s^{\prime}\) 的值函数近似估计：

\[\hat G\left( {{\tau _{t:T}}} \right) = {r_{t + 1}} + \gamma {V_\phi }\left( {{s_{t + 1}}} \right) \tag{1-1} \]

来看一下李宏毅课程的解释，在上一节策略梯度中得到 $\mathbb{E}\left[G\left(\tau_{t : T}\right)\right]={Q^{{\pi _\theta }}}\left( {{s_t},{a_t}} \right) $，所以说我们需要的 \(G\) 的期望其实就是状态-动作值函数，而状态-动作值函数和状态值函数的关系为：

\[Q^{\pi_{\theta}}(s_t, a_t)=\mathbb{E}_{s_{t+1} \sim p_{\theta}\left(s_{t+1} | s_t, a_t\right)}\left[r\left(s_t, a_t, s_{t+1}\right)+\gamma {V_\phi} \left( {{s_{t + 1}}} \right) \right] \tag{1-2} \]

现在我们把 (2) 中的期望拿掉了，就得到了 (1) 式.

为什么拿掉呢？李宏毅课上说原作者实验了很多次，发现拿掉后结果比较好，很玄学。

2 算法流程

在演员-评论员算法中的策略函数(演员) \(\pi _\theta\left( {a|s} \right)\) 和值函数(评论员) \({V_\phi }\left( {{s_t}} \right)\) 都是待学习的函数。

在每步更新中，一方面需要更新参数 \(\phi\) 使得值函数 \({V_\phi }\left( {{s_t}} \right)\) 接近于估计的真实回报 \(\hat G\left( {{\tau _{t:T}}} \right)\). 这个真实回报是演员在当前环境 $s_t $ 下执行动作 $a_t $ 后得到的即时奖励，再加上评论员使用之前标准对新状态 \(s_{t+1}\)的打分来近似的：\({r_{t + 1}} + \gamma {V_\phi }\left( {{s_{t + 1}}} \right)\).

\[\begin{aligned} & \min _{\phi}\left(\hat{G}\left(\tau_{t: T}\right)-V_{\phi}\left(s_{t}\right)\right)^{2} \\ =& \min _{\phi}\left(r_{t+1}+\gamma V_{\phi}\left(s_{t+1}\right)-V_{\phi}\left(s_{t}\right)\right)^{2} \end{aligned} \tag{2-1} \]

评论员来根据这个误差来调整自己的打分标准，使得自己的评分更接近于环境的真实回报。

另一方面，演员需要根据评论员的打分调整自己的策略 \(\pi_\theta\). 即将值函数 \({V_\phi }\left( {{s_t}} \right)\) 带入策略函数的梯度公式：

\[\nabla J(\theta ) \approx \frac{1}{N}\sum\limits_{n = 1}^N {\sum\limits_{t = 0}^{T - 1} {\left[ { \gamma^{t}\left(r^{(n)}_{t+1}+\gamma V_{\phi}\left(s_{t+1}\right)\right) - {V_\phi }\left( {{s_t}} \right)} \right]\nabla } \log {\pi _\theta }\left( {a_t^{(n)}|s_t^{(n)}} \right)} \tag{2-2} \]

所以每步参数 \(\theta\) 的更新公式为(计算每个时刻的梯度就开始更新参数了)：

\[\theta \leftarrow \theta+\alpha \gamma^{t}\left[r_{t+1}+\gamma V_{\phi}\left(s_{t+1}\right)-V_{\phi}\left(s_{t}\right)\right] \nabla \log \pi_{\theta}\left(a_{t} | s_{t}\right) \tag{2-3} \]

具体的算法流程如下：

Actor-Critic算法

3 参考资料

1. 神经网络与深度学习-邱锡鹏
2. 李宏毅主页