策略梯度(Policy Gradient)

对于DQN来说使用一个网络直接逼近了值函数，最后取得了非常不错的效果, 但是对于一些连续性控制或者动作空间特别大的环境来说，很难全部计算所有的值函数来得到最好的策略，那么直接计算策略的方法就别提出来了。

1 策略梯度理论

在Value Based的方法中，我们迭代计算的是值函数，然后根据值函数对策略进行改进；而在Policy Based方法中，我们直接对策略 \({\pi _\theta }\left( {a|s} \right)\) 进行迭代计算，直到累积回报的期望最大，此时的参数所对应的策略为最优策略。

下图来自周博磊老师的课件\(^{[2]}\)，左边就是基于策略的方法，可以看出每到一个地方(state)就会得到一个方向(action)。右边是基于值得方法，当到一个地方时，需要计算一下周围哪个地方的值函数更大，就会往那走。

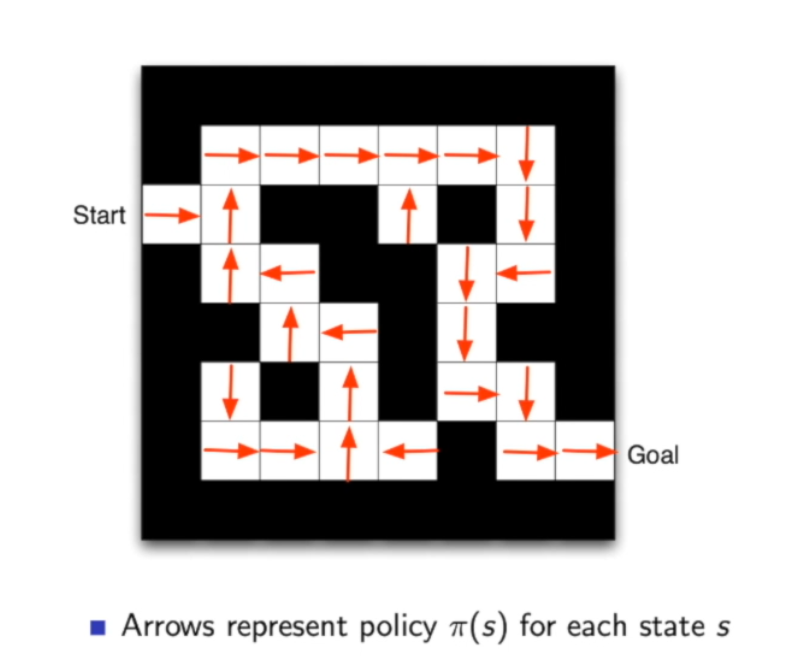
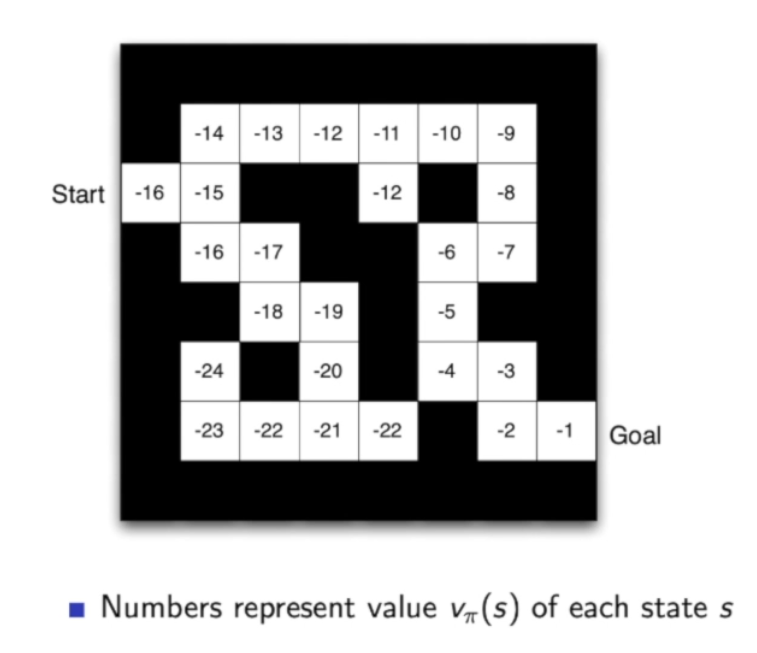
下面用 \(\tau\) 来表示一个轨迹：\(\tau = {s_0},{a_0},{s_1},{a_1} \ldots {s_T}\). 对于给定策略，智能体和环境进行一次轨迹为 \(\tau\) 的交互，收到的总回报为：

\[G\left( \tau \right) = \sum\limits_{t = 0}^{T - 1} {{\gamma ^t}{r_{t + 1}}} \tag{1-1} \]

由于策略和状态转移都有一定的个随机性，所以每次的轨迹也是随机的，我们希望基于策略的方法能够学习到一个最佳策略 \(\pi _\theta^{*} \left( {a|s} \right)\) 来最大化这个总回报的期望：

\[\begin{aligned} J\left( \theta \right) &= {\mathbb{E}_{\tau \sim{p_\theta }\left( \tau \right)}}\left[ {G\left( \tau \right)} \right]\\ &= \int {{p_\theta }\left( \tau \right)} G\left( \tau \right)d\tau \end{aligned} \tag{1-2} \]

对这个目标函数 \(J\left( \theta \right)\) 求关于参数 \(\theta\) 的偏导为：

\[\begin{aligned} \nabla J\left( \theta \right) &=\frac{\partial}{\partial \theta} \int p_{\theta}(\tau) G(\tau) \mathrm{d} \tau \\ &=\int\left(\frac{\partial}{\partial \theta} p_{\theta}(\tau)\right) G(\tau) \mathrm{d} \tau \\ &=\int p_{\theta}(\tau)\left(\frac{1}{p_{\theta}(\tau)} \frac{\partial}{\partial \theta} p_{\theta}(\tau)\right) G(\tau) \mathrm{d} \tau \\ &=\int p_{\theta}(\tau)\left(\frac{\partial}{\partial \theta} \log p_{\theta}(\tau)\right) G(\tau) \mathrm{d} \tau \\ &=\mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[\nabla \log p_{\theta}(\tau) G(\tau)\right] \end{aligned} \tag{1-3} \]

进一步求解 \(\nabla \log p_{\theta}(\tau)\) 可得：

\[\begin{aligned} \nabla & \log p_{\theta}(\tau)=\frac{\partial}{\partial \theta} \log \left(p\left(s_{0}\right) \prod_{t=0}^{T-1} \pi_{\theta}\left(a_{t} | s_{t}\right) p\left(s_{t+1} | s_{t}, a_{t}\right)\right) \\ &=\frac{\partial}{\partial \theta}\left(\log p\left(s_{0}\right)+\sum_{t=0}^{T-1} \log \pi_{\theta}\left(a_{t} | s_{t}\right)+\sum_{t=0}^{T-1} \log p\left(s_{t+1} | s_{t}, a_{t}\right)\right) \\ &=\sum_{t=0}^{T-1} \nabla \log \pi_{\theta}\left(a_{t} | s_{t}\right) \end{aligned} \tag{1-4} \]

可以看出 \(\nabla \log p_{\theta}(\tau)\) 只和策略函数 \({\pi _\theta }\left( {a|s} \right)\) 相关，和状态转移概率 \(p\left(s_{t+1} | s_{t}, a_{t}\right)\) 无关。把式 (1-4) 带入 (1-3) 可得到：

\[\begin{aligned} \nabla {J}(\theta) &=\mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[\left(\sum_{t=0}^{T-1} \nabla \log \pi_{\theta}\left(a_{t} | s_{t}\right)\right) G(\tau)\right] \\ &=\mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[\left(\sum_{t=0}^{T-1} \nabla \log \pi_{\theta}\left(a_{t} | s_{t}\right)\right)\left( \sum\limits_{t = 0}^{T - 1} {{\gamma ^t}{r_{t + 1}}} \right)\right] \\ &=\mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t=0}^{T-1}\left(\nabla \log \pi_{\theta}\left(a_{t} | s_{t}\right) \gamma^{t} G\left(\tau_{t: T}\right)\right)\right] \end{aligned} \tag{1-5} \]

这里定义 \(G\left(\tau_{t: T}\right)\) 为把时刻 \(t\) 当成起始时刻收到的总回报：

\[G\left(\tau_{t: T}\right)=\sum_{t^{\prime}=t}^{T-1} \gamma^{t^{\prime}-t} r_{t^{\prime}+1} \tag{1-6} \]

公式 (1-5) 从第二步得到第三步也就是李宏毅课中\(^{[3]}\)讲的Tip2，即时刻 \(t\) 之前的回报和时刻 \(t\) 之后的动作无关。这个在直觉上很好理解，今天老板看到你工作努力想给你奖赏，老板不会给你昨天的工资加倍，只会给你今天的工资或者未来的工资加倍。证明如下：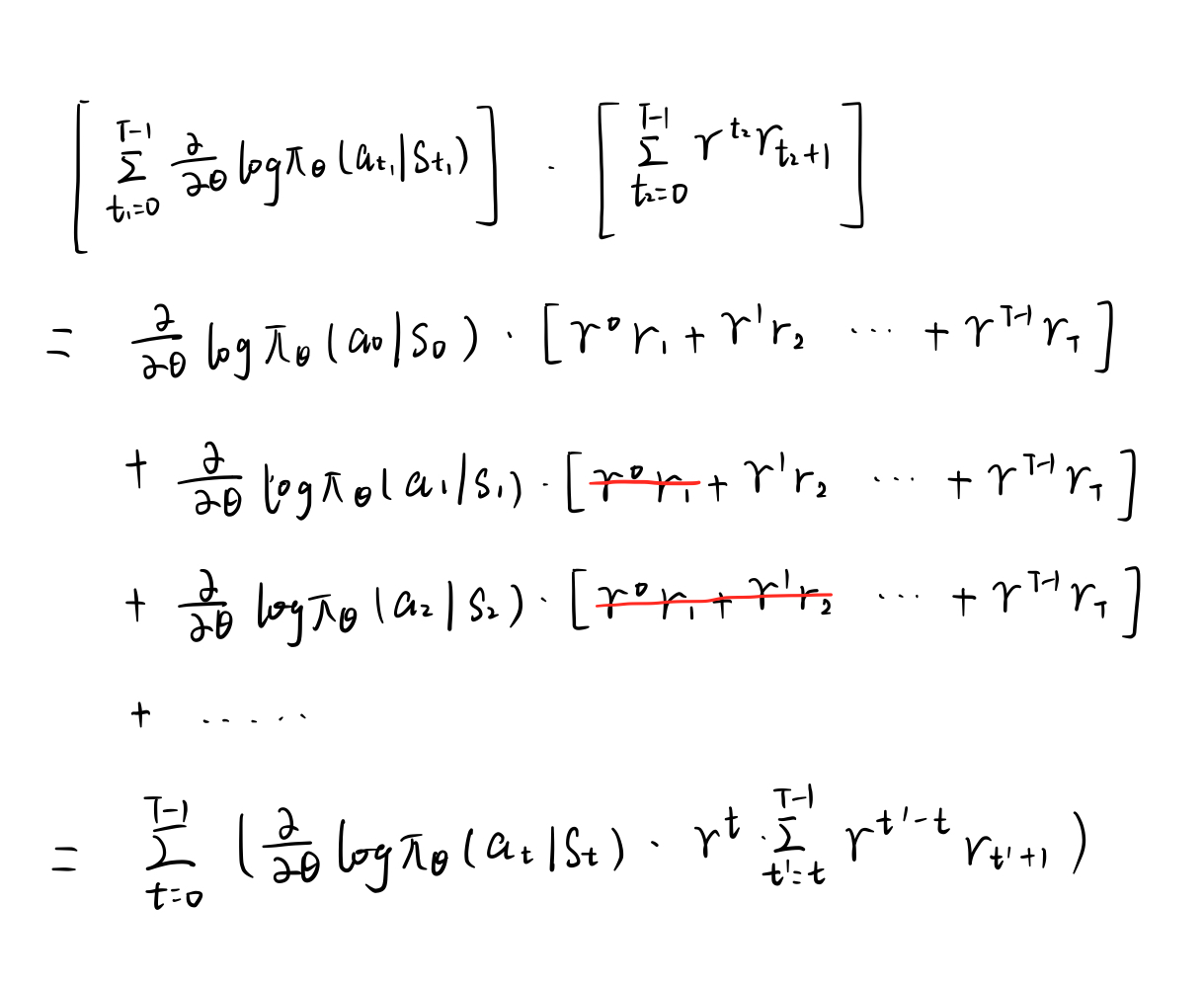

公式(1-5)证明

2 REINFORCE 算法

公式 (1-5) 中的 \(\nabla {J}(\theta)\) 是用期望表示的，期望可以通过采样的方法来近似。可以根据当前的策略 \(\pi _\theta\) 通过游走采集多条轨迹 \({\tau ^{\left( {\rm{1}} \right)}},{\tau ^{\left( 2 \right)}}, \ldots {\tau ^{\left( N \right)}}\). 其中一条轨迹 ${\tau ^{\left( n \right)}} = s_0^{\left( n \right)},a_0^{\left( n \right)},s_1^{\left( n \right)},a_1^{\left( n \right)}, \ldots $ 所以 \(\nabla {J}(\theta)\) 可以写成：

\[\nabla {J}(\theta) \approx \frac{1}{N} \sum_{n=1}^{N}\left(\sum_{t=0}^{T-1} \nabla \log \pi_{\theta}\left(a_{t}^{(n)} | s_{t}^{(n)}\right) \gamma^{t} G^{(n)}\left(\tau_{t: T}\right)\right) \tag{2-1} \]

有了策略梯度的计算公式就可以更新梯度了：

\[\hat \theta = \theta + \alpha \nabla J\left( \theta \right) \tag{2-2} \]

邱锡鹏老师书上的具体的算法如下：

REINFORCE算法

可以看出其实是每采集一条轨迹，计算每个时刻的梯度就开始更新参数了

3 带基准线的 REINFORCE 算法

假如在状态 \(s_t\) 下有三个动作 \(a,b,c\)，其概率之和为1。如果执行这个动作后得到正的总回报 \(G\left( \tau \right)\)，则需要增大这个动作被选中的概率，如果得到负的总回报则减小其概率。

在理想情况下，三个动作都被采样到了，可以看出他们的总回报 \(G\left( \tau \right)\) 全都是正的值。然而这三个动作的总概率为1，所以被选中的概率不能全都增大，肯定是有的增大有的减小。所以只能哪个动作得到的总回报更多，就让它的概率大一点。

然而在实际中，不可能采样到所有的动作，假如动作 \(a\) 没被采到，动作 \(b,c\) 得到的回报都是正的值。这样在下一个回合选中动作 \(b,c\) 的概率都会上升，而选中动作 \(a\) 的概率会下降。但这并不代表动作 \(a\) 一定不好，只是没有采样到。

Sampling the actions

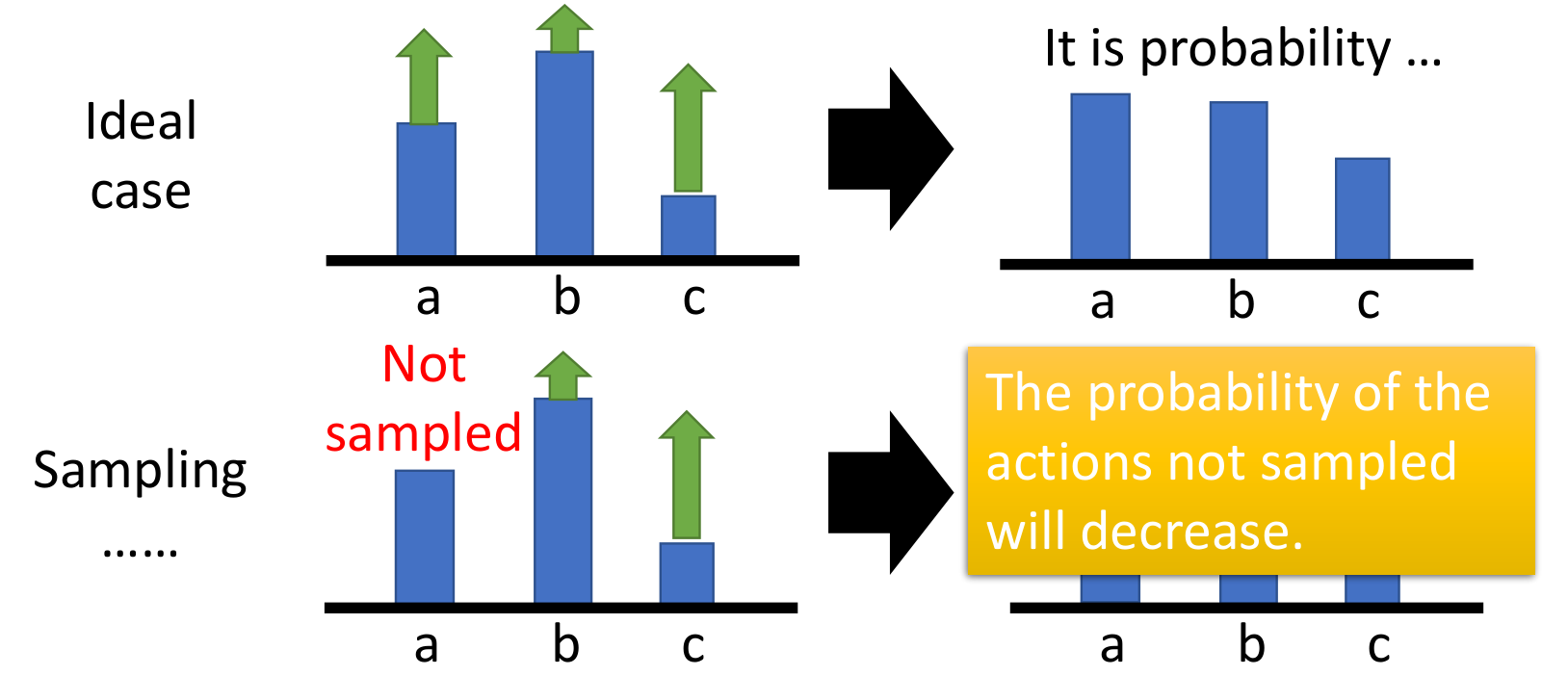
解决办法：减去一个固定值 \(b(s_t)\)，让各个动作对应的奖励有正有负。一个常用的选择是令 \(b(s_t)\) 为这个状态的值函数 \({V^{{\pi _\theta }}}\left( {{s_t}} \right)\).

邱锡鹏老师的书上有证明\(^{[1]}\)，虽然减去了一个和 \(s_t\) 相关的固定值，但是并没有影响 \(\nabla {J}(\theta)\)，也就是说参数 \(\theta\) 更新的规则是不变的.

需要注意的两点是：

1. 其实这个值函数 \({V^{{\pi _\theta }}}\left( {{s_t}} \right)\) 是不知道的，可以用监督学习的办法来做，用学习得到的函数 \({V_\phi }\left( {{s_t}} \right)\) 来近似表示 \({V^{{\pi _\theta }}}\left( {{s_t}} \right)\) . 另外 \(Loss \ function\) 定义为：

   \[L\left( \phi \right) = {\left( {{V^{{\pi _\theta }}}\left( {{s_t}} \right) - {V_\phi }\left( {{s_t}} \right)} \right)^2} \tag{3-1} \]

2. 问题又来了，上面 \(Loss\) 的定义需要用到值函数 \({V^{{\pi _\theta }}}\left( {{s_t}} \right)\)，但是我们又不知道值函数。先来看一下值函数的定义：

   \[V^{\pi_{\theta}}\left(s_{t}\right)=\mathbb{E}\left[G\left(\tau_{t : T}\right)\right] \tag{3-2} \]

   实际上所采取的办法是用蒙特卡罗方法进行估计(用经验平均代替期望)，在算法执行的时候好像更简便，直接用一次采样代表期望了。

有了上面两点，就可以对学习的函数 \({V_\phi }\left( {{s_t}} \right)\) 采用梯度下降法更新，参数 \(\phi\) 的梯度为：

\[\frac{\partial L\left(\phi | s_{t}, \pi_{\theta}\right)}{\partial \phi}=-\left(G\left(\tau_{t: T}\right)-V_{\phi}\left(s_{t}\right)\right) \frac{\partial V_{\phi}\left(s_{t}\right)}{\partial \phi} \tag{3-3} \]

有了这个基准线 \({V_\phi }\left( {{s_t}} \right)\) 就可以把策略函数的梯度公式 (2-1) 改写为:

\[\nabla J(\theta ) \approx \frac{1}{N}\sum\limits_{n = 1}^N {\sum\limits_{t = 0}^{T - 1} {\left( {{\gamma ^t}{G^{(n)}}\left( {{\tau _{t:T}}} \right) - {V_\phi }\left( {{s_t}} \right)} \right)\nabla } \log {\pi _\theta }\left( {a_t^{(n)}|s_t^{(n)}} \right)} \tag{3-4} \]

在上面的第二点中关于这个 \(\mathbb{E}\left[G\left(\tau_{t : T}\right)\right]\) 的定义其实还有点疑问，邱锡鹏老师这个做法和李宏毅的做法不太一样，李宏毅是定义 \({Q^{{\pi _\theta }}}\left( {{s_t},{a_t}} \right) = \mathbb{E}\left[G\left(\tau_{t : T}\right)\right]\). 其实李宏毅课程中这么定义也是有道理的，因为这个 \(G\left(\tau_{t: T}\right)\) 其实是总回报，他是来衡量在状态 \(s_t\) 执行动作 \(a_t\) 后得到的总奖励，然后来判定这个动作 \(a_t\) 好不好。所以说这个动作是执行过了，才能得到 \(G\). 这个定义在后面Actor-Critic还要用到，个人更偏向于李宏毅老师的定义。

\(\left\{ \begin{array}{l} {V^{{\pi _\theta }}}\left( {{s_t}} \right) = \left[ {\left. {G\left( {{\tau _{t:T}}} \right)} \right|{s_t}} \right]\\ {Q^{{\pi _\theta }}}\left( {{s_t},{a_t}} \right) = \left[ {\left. {G\left( {{\tau _{t:T}}} \right)} \right|{s_t},{a_t}} \right] \end{array} \right.\)

下面来看一下具体的算法：

带基准线的REINFORCE算法

4 参考资料

1. 神经网络与深度学习-邱锡鹏
2. 强化学习纲要-周博磊
3. 李宏毅强化学习课程
4. 智能单元
5. 机器学习笔记-知乎专栏
6. Robot Learning-策略梯度（Policy Gradient）