无约束优化问题

线性搜索下降算法

• Step 0：给定初始点\(x^0\)，\(k=0\)；
• Step 1：判断\(x^k\)是否满足终止条件，满足则终止；
• Step 2：寻找\(x^k\)处的下降方向\(d^k\)；
• Step 3：选择合适的步长\(\alpha^k>0\)，使得\(f(x^k+\alpha_k d^k)<f(x^k)\)；
• Step 4：令\(x^{k+1}=x^k+\alpha_kd^k\)，\(k=k+1\)，转向Step 1.

1. 常用的终止准则：\(\left\|\nabla f\left(x^{k}\right)\right\| \leq \epsilon\)
2. 选择步长：基于区间的直接搜索法、非精确搜索准则；
3. 下降方向：不同的下降方向选取方式就有了不同的算法
4. 收敛性、收敛速度

1 坐标轴交替下降法

基本思想：给定初始点\(x^0\)，依次沿着坐标轴\(e_1,\dots e_n\)进行搜索

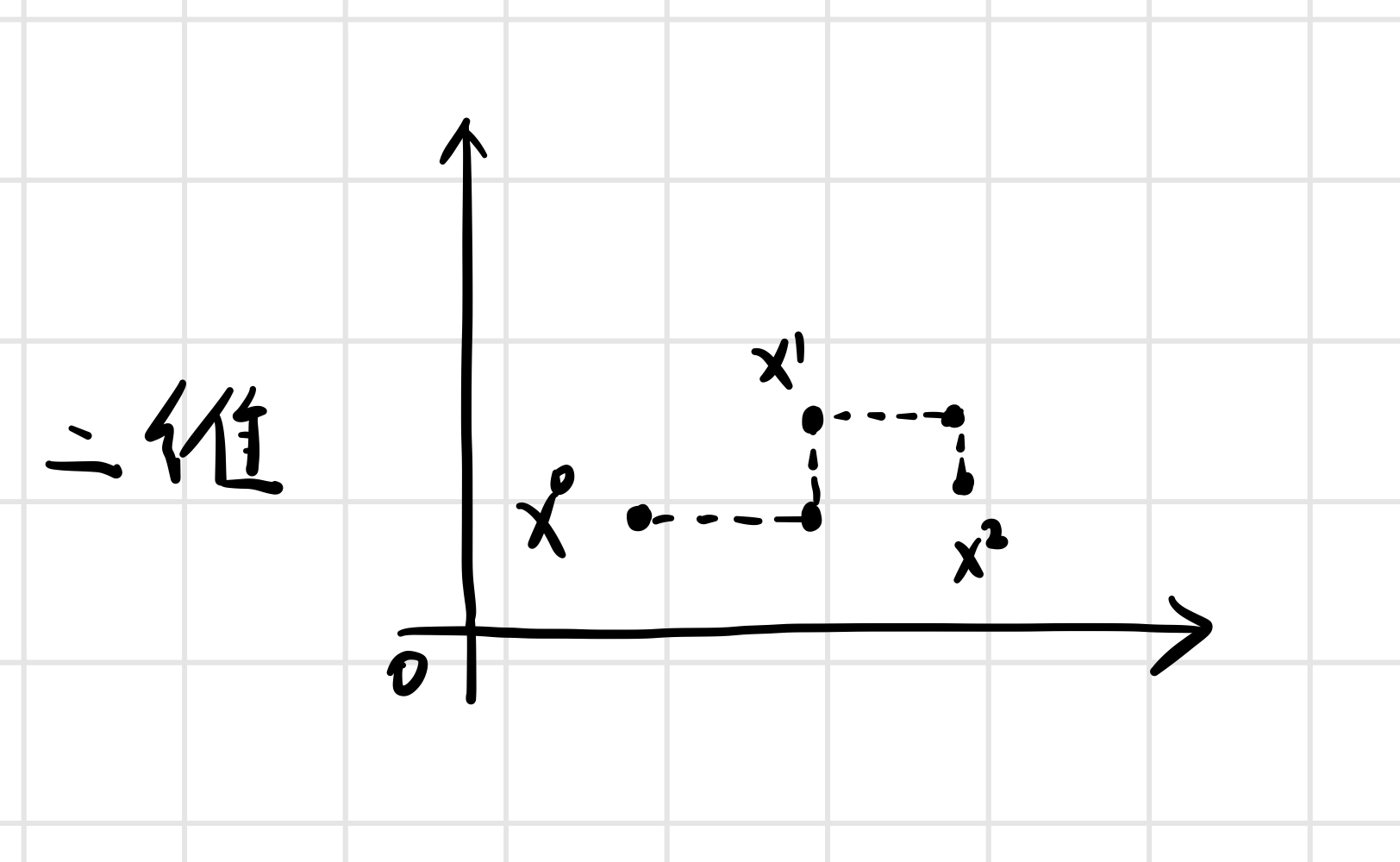
1. 给定初始点\(x^0\)，\(k=0\)；
2. 判断是否满足\(\left\|\nabla f\left(x^{k}\right)\right\| \leq \epsilon\)，满足则终止；
3. 记\(y_0=x^k\)，令\(y_i=y_{i-1}+\alpha_ie_i\)，其中\(\alpha_{i}=\arg \min f\left(y_{i-1}+\alpha e_{i}\right), i=1, \cdots, n\)
4. 令\(x^{k+1}=y_n\)，\(k=k+1\)，转到第2步

当变量之间的交叉程度较小时非常有效，比如：

\[\min f(x)=f_1(x_1)+f_2(x_2)+\dots+f_n(x_n) \]

2 最速下降法（梯度下降法）

基本思想：选择\(x^k\)处负梯度作为搜索方向，即\(d^{k}=-\nabla f\left(x^{k}\right)\)

若迭代步长\(\alpha_k\)是\(\phi(\alpha)=f(x^k+\alpha_k d^k)\)的精确最小点，则\(\phi^{'}(\alpha_k)=0\)，即：

\[\phi^{'}(\alpha_k)=-\nabla f\left(x^{k+1}\right)^{T}\nabla f\left(x^{k}\right)=0 \]

例：\(\min f(x)=0.5x_1^2+2x_2^2\)，设初始点\(x^0=(2,1)^T\)

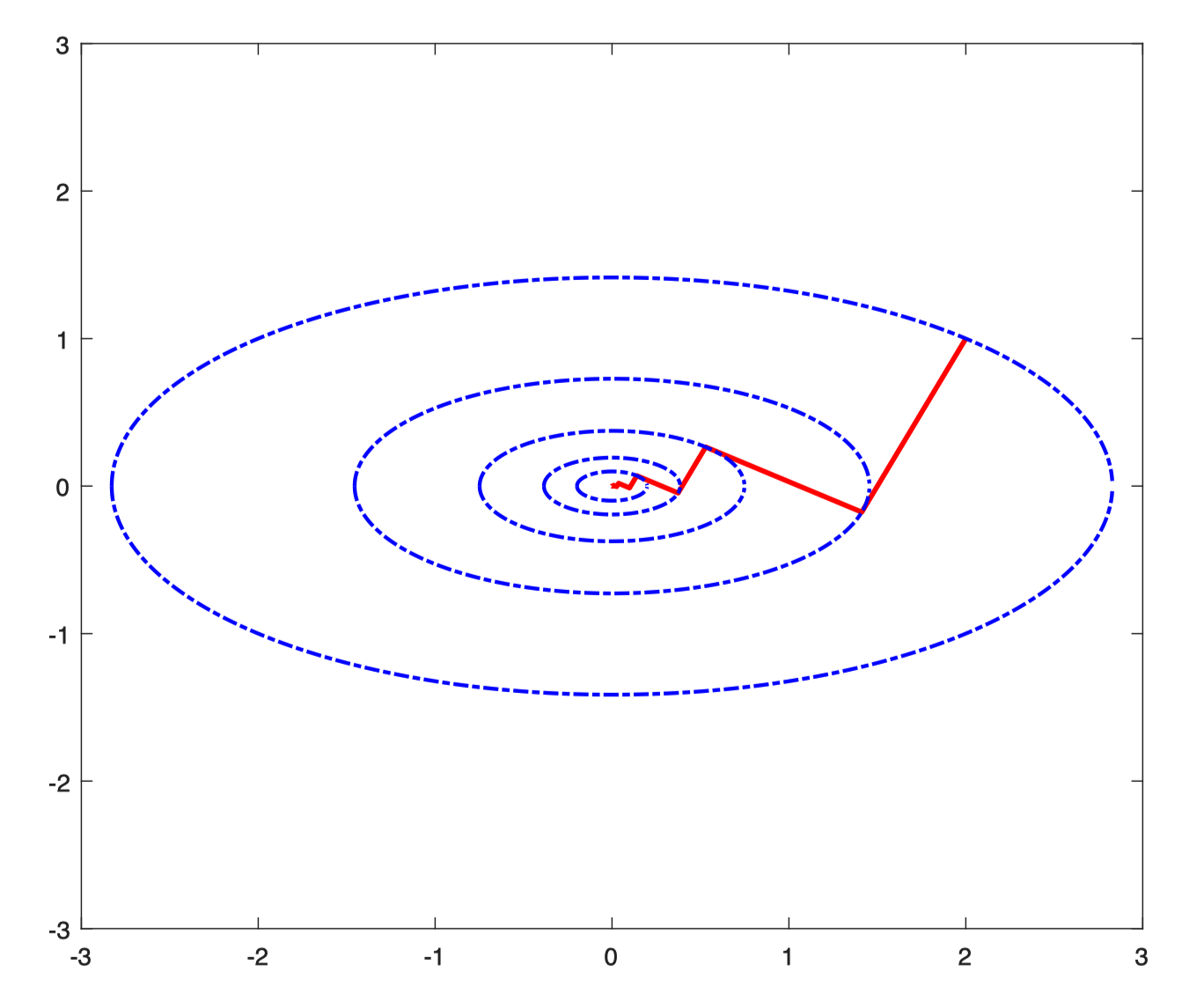
缺点：

• 收敛速度慢（线性收敛）
• 不具备二次终止性，即在有限步内求得凸二次函数最优解

3 牛顿法

基本思想：对\(x^k\)处的二次逼近函数进行最小化：

\[\min f\left(x^{k}\right)+\nabla f\left(x^{k}\right)^{T}\left(x-x^{k}\right)+1 / 2\left(x-x^{k}\right)^{T} \nabla^{2} f\left(x^{k}\right)\left(x-x_{k}\right) \]

对二次近似函数进行求导：

\[\nabla f\left(x^{k}\right)+\nabla^2 f\left(x^{k}\right)\left(x-x^{k}\right)=0 \]

进行移项可得：

\[x^{k+1}=x^k-[\nabla^2 f\left(x^{k}\right)]^{-1}\nabla f\left(x^{k}\right) \]

牛顿法步骤：

1. 给定初始点\(x^0\)，\(k=0\)；
2. 判断是否满足\(\left\|\nabla f\left(x^{k}\right)\right\| \leq \epsilon\)，满足则终止；
3. 计算\(d^k=-[\nabla^2 f\left(x^{k}\right)]^{-1}\nabla f\left(x^{k}\right)\)，步长\(\alpha_k=1\)
4. \(x^{k+1}=x^k+d^k\)

优缺点：

• 牛顿方向\(d^k=-[\nabla^2 f\left(x^{k}\right)]^{-1}\nabla f\left(x^{k}\right)\)只有在\(\nabla^2 f\left(x^{k}\right)\)正定时才是下降方向
• 当初始点\(x^0\)取得比较接近于收敛点\(x^*\)时，且\(\nabla^2 f\left(x^{k}\right)\)具有较好的性质，二阶收敛
• 计算量大，需要计算Hesse矩阵

4 修正牛顿法

• 对步长\(\alpha_k\)的修正：首先判断\(\alpha_k=1\)是否让目标函数充分下降，否则采用线搜索方法重新确定\(\alpha_k\)

• 对于方向（Hesse矩阵）的修正：选取\(d^k=-B_k^{-1}\nabla f\left(x^{k}\right)\)

  • 若\(\nabla^2 f\left(x^{k}\right)\succ 0\)，则选取\(B_k=\nabla^2 f\left(x^{k}\right)\)

  • 否则修正方法有多种：

    1. \(B_k=\nabla^2 f\left(x^{k}\right)+\lambda I\)，\(\lambda\)为适当正数保证\(B_k\)正定

    2. 考虑特征值分解\(\nabla^{2} f\left(x^{k}\right)=Q^{T} \Sigma Q\) ，其中$ \Sigma=dia g(\lambda_1,\cdots,\lambda_n)$ ，每一个对角线元素就是一个特征值。令\(B_k=Q^{T} diag(\tau_i) Q\)

       \[\tau_{i}=\left\{\begin{array}{ll} \lambda_{i}, & \text { if } \lambda_{i} \geq \delta ; \\ \delta, & \text { otherwise } \end{array}, \delta\right. \text { 为一适当的正数 } \]

5 拟牛顿法

考虑\(f(x)\)在当前点\(x^k\)处的二次近似函数

\[m_k(x)=f\left(x^{k}\right)+\nabla f\left(x^{k}\right)^{T}\left(x-x^{k}\right)+1 / 2\left(x-x^{k}\right)^{T} B_k\left(x-x_{k}\right) \]

其中\(B_k\succ 0\)，这个\(B_k\)就是为了代替\(\nabla^2 f\left(x^{k}\right)\)的，因为Hesse矩阵不好求

利用\(\min m_k(x)\)得到搜索方向\(d^k=-B_k^{-1}\nabla f\left(x^{k}\right)\)

拟牛顿法步骤：

1. 给定初始点\(x^0\)，\(B_0\succ 0\)，\(k=0\)；
2. 判断是否满足\(\left\|\nabla f\left(x^{k}\right)\right\| \leq \epsilon\)，满足则终止；
3. 计算方向\(d^k=-B_k^{-1}\nabla f\left(x^{k}\right)\)
4. 确定步长\(\alpha_k\)
5. 令\(x^{k+1}=x^k+d^k\)，确定\(B_{k+1}\)，\(k=k+1\)，转到第2步

在\(x^{k+1}\)这个点确定\(B_{k+1}\)有多种方法，如何简便获取矩阵\(B_{k+1}\)？

在\(x^{k}\)点处已知\(\nabla f\left(x^{k}\right)\)和\(B_k\)，此时刚得到\(x^{k+1}\)点，可以计算出该点的梯度\(\nabla f\left(x^{k+1}\right)\)，待求的为\(B_{k+1}\)。根据中值定理可知：

\[\nabla f\left(x^{k+1}\right)-\nabla f\left(x^{k}\right)=\nabla^2 f\left(\xi \right)(x^{k+1}-x^k), \quad \xi=\lambda x^{k}+(1-\lambda)x^{k+1},\lambda\in(0,1) \]

这个Hesse矩阵\(\nabla^2 f\left(\xi \right)\)不好算，所以用\(B_{k+1}\)来代替，所以基本要求是：

\[\nabla f\left(x^{k+1}\right)-\nabla f\left(x^{k}\right)=B_{k+1}(x^{k+1}-x^k) \]

这个就是拟牛顿方程，满足拟牛顿方程的矩阵有很多。

• 记\(y_k=\nabla f\left(x^{k+1}\right)-\nabla f\left(x^{k}\right)\)，\(s_k=x^{k+1}-x^{k}\)，则上式简写为：\(y_k=B_{k+1}s_k\)

• 记\(H_k=B_k^{-1}\)，拟牛顿方程也可以表示成\(s_k=H_{k+1}y_k\)

基于已有信息\(y_k,s_k,B_k\)获取\(B_{k+1}\)有几种方法：

• 第一类方法：选择满足拟牛顿方程且与\(B_k\)近似的矩阵

  \[\min \| B-B_{k} \|, \text { s.t. } B s_{k}=y_{k}, B=B^{T} \]

• 第二类方法：对\(B_k\)（或者\(H_k\)）进行校正，如：\(B_{k+1}=B_k+\Delta B\)

  • rank-2校正，要求\(\Delta B\)的秩为2，有DFP方法，BFGS方法
  • rank-1校正，要求\(\Delta B\)的秩为1

6 共轭方向法

共轭方向：考虑正定矩阵\(Q\)及非零向量\(d^i,d^j\)。若\((d^i)^TQd^j=0\)，则称\(d^i,d^j\)关于矩阵\(Q\)共轭。

对于问题：

\[\min f(x)=1 / 2 x^{T} Q x+c^{T} x, \quad Q \succ 0 \]

给定初始点\(x^0\)及一组关于\(Q\)共轭方向\(d^0,d^1,\cdots,d^{n-1}\)，令\(x^{k+1}=x^k+\alpha_kd^k, \quad k=0,\cdots ,n-1\)

其中

\[\alpha_{k}=\arg \min \phi(\alpha)=f\left(x^{k}+\alpha d^{k}\right) \]

对\(\phi(\alpha)\)求导可得到

\[\alpha_{k}=-\frac{\left(Q x^{k}+c\right)^{T} d^{k}}{\left(d^{k}\right)^{T} Q d^{k}}=-\frac{\nabla f\left(x^{k}\right)^{T} d^{k}}{\left(d^{k}\right)^{T} Q d^{k}} \]

共轭方向法为一类方法，共轭梯度法是其中一种。

几何解释：

对于问题

\[\min f(x)=1 / 2 x^{T} Q x+c^{T} x, \quad Q \succ 0 \]

• 当\(Q\)是一个对角阵时，\(f(x)=1 / 2 x^{T} \rm diag(q_{11},\cdots q_{nn}) x+c^{T}\)，可以发现\(f(x)\)没有交叉的项（即\(x_{ij},i\not=j\)），所以这时沿着每个维度去正交搜索就行了（作一次精确线搜索就可以得到这个维度上最小值的精确解），比如下图\(n=2\)时：

  

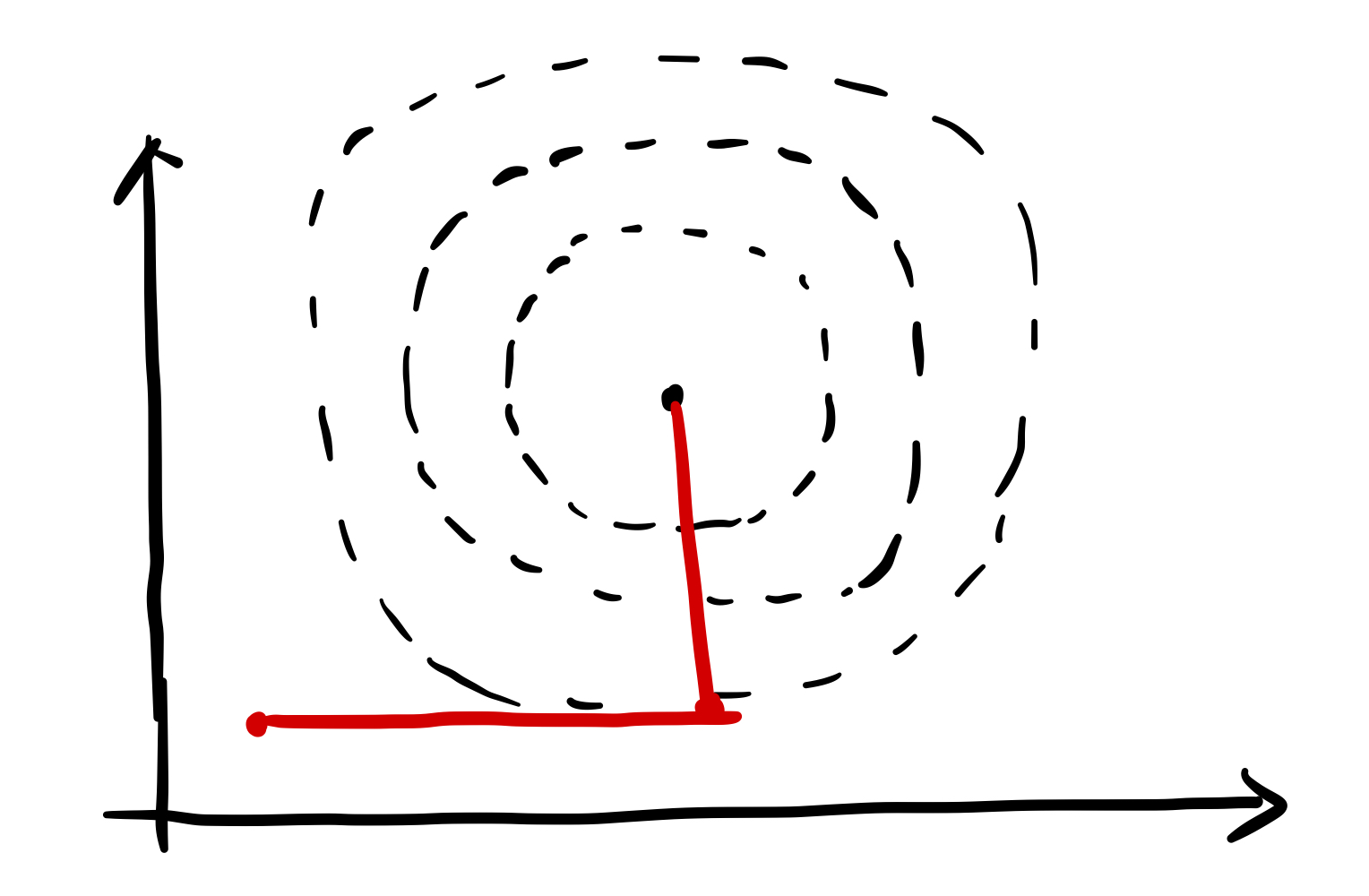
• 而\(Q\)不是对角阵时

  令\(S=(d^0,d^1,\cdots,d^{n-1})\)，\(S\)可逆，可以发现此时

  \[\hat Q = S^TQS= \left(\begin{array}{c} \left(d^{0}\right)^{\top} \\ \cdots \\ \left(d^{n-1}\right)^{T} \end{array}\right) Q\left(d^{0} \cdot \cdot \cdot d^{n-1}\right) \]

  根据共轭的性质可以知道，\(\hat Q\)一个对角阵。因此令\(x=S\hat{x}\)，上面的问题中\(f(x)\)可以写为：

  \[\begin{aligned} f(\hat x)& =1 / 2\hat x^{T}S^T Q S \hat x+(S^Tc)^{T} \hat x \\ & = 1 / 2\hat x^{T} \hat Q \hat x+(S^Tc)^{T} \hat x \end{aligned} \]

  此时变成了在\(\hat x\)坐标域上进行搜索。

7 共轭梯度法

在迭代下降过程中，借助当前点\(x^k\)的梯度信息构造共轭方向\(d^k\)

共轭梯度法步骤：

1. 给定初始点\(x^0\)，记\(d^0=-\Delta f(x^0)\)，\(k=0\)

2. 判断是否满足\(\left\|\nabla f\left(x^{k}\right)\right\| \leq \epsilon\)，满足则终止；

3. 利用线性搜索计算步长\(\alpha_k\)（上面有计算公式）；

4. 令\(x^{k+1}=x^k + \alpha_k d^k\)，并计算方向

   \[d^{k+1}=-\Delta f(x^{k+1})+\beta_kd^k \]

   其中

   \[\beta_{k}=\frac{\nabla f\left(x^{k+1}\right)^{T} \nabla f\left(x^{k+1}\right)}{\nabla f\left(x^{k}\right)^{T} \nabla f\left(x^{k}\right)} \]

   令\(k=k+1\)，转第2步