为什么要用等效基带信号?
1.1 单边带信号与 IQ 调制
1.1.1 单边带信号的产生
双边带信号占用带宽比较多,造成很大的浪费。假设双边带信号的频谱为 \(S\left( \omega \right)\),把两倍的阶跃信号与基带信号的频谱相乘,可以得到基带的单边带信号:
前面这个 2 的系数是为了使调制后的射频信号形式更简单。
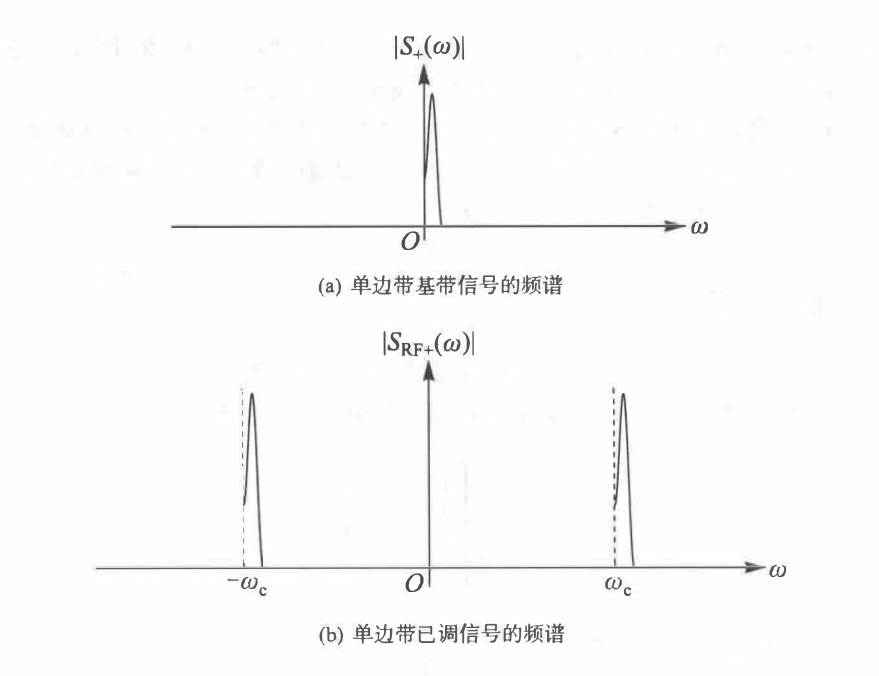
对 \({S_ + }\left( \omega \right)\) 做傅里叶反变换,我们可以求出单边带基带信号的时域形式:
这里的证明用到了 \(2u\left( \omega \right) = 1 + Sgn\left( \omega \right)\),式子 \(s\left( t \right) * \frac{1}{{\pi t}}\) 的运算是对 \(s\left( t \right)\) 的希尔伯特变换,记为 \(\hat s\left( t \right)\)。
这样从双边带基带信号 \(s\left( t \right)\) 就可以通过以下方式得到一个单边带基带信号:
1.1.2 单边带信号的发送
在通信原理中课本上是直接给出了单边带调制信号的表达式,但是没有给过程。首先我们假设双边带基带信号 \(s\left( t \right) = {A_0}\cos \left( {{\omega _0}t} \right)\),对这个信号进行载波调制,我们得到双边带调制信号 \({s_{DSB}}\left( t \right)\):
而我们得到的单边带调制信号(以下边带为例):
我们来看一下这个单边带调制信号实际上是怎么从单边带基带信号得到的。
上一节我们得到单边带基带信号:\({s_ + }\left( t \right) = s\left( t \right) + j\hat s\left( t \right)\),从表达式上来看,这其实是个复数信号。然而在实际电路中,所有信号都是实数,如何表达一个复数信号呢?一个复数 \(x + jy\) 是和一个实数对 \(\left( {x,y} \right)\) 相对应,也就是说一个实数对就可以表达一个复数。
当我们用载波信号 \(\cos \left( {{\omega _c}t} \right)\) 与单边带基带信号相乘后得到:
虽然 \({s_{RF + }}\left( t \right)\) 是一个单边带已调信号(这个频谱图在上面有),但是他的实部和虚部其实都是双边带信号,而且他们之间也没有什么联系。那么我们可以采用复指数信号为载波,得到一个单边带的已调信号,为了符号方便,我们仍用 \({s_{RF + }}\left( t \right)\) 表示:
我们来看一下这个信号实部的频谱图:
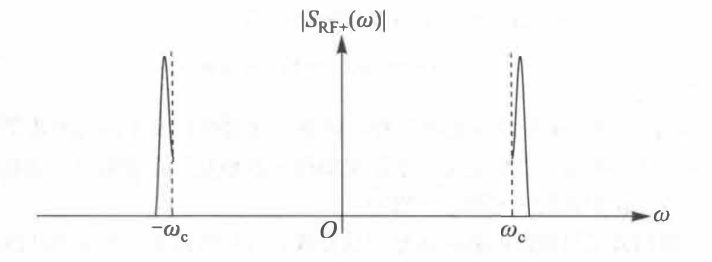
这其实就是双边带信号经过边带滤波后得到的上边带信号,即 \({s_{USB}}\left( t \right)\)。而虚部所含的信息和实部其实是一样的,虚部部分其实就是下边带信号,即 \({s_{LSB}}\left( t \right)\)。
从频谱上来看 \(s\left( t \right)\cos \left( {{\omega _c}t} \right)\) 是双边带频谱,而 \(s(t)\cos \left( {{\omega _c}t} \right) - \hat s(t)\sin \left( {{\omega _c}t} \right)\) 是单边带频谱,这其实是因为单边带信号同时利用了载波的幅度和相位,而双边带信号只利用了载波的幅度。或者等价地说,双边带信号只利用了余弦分量,而单边带信号同时利用了正弦和余弦两个正交分量。
这样的话,我们就找到了单边带信号的发射方案,只要发射实部或者虚部就可以了,一般我们发射实部部分[1]。
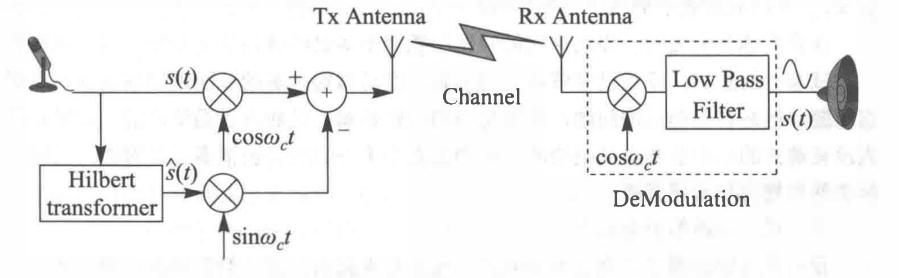
1.1.3 IQ调制
为了实现恰好将双边带信号的一个边带消掉的目的,单边带信号的正弦和余弦分量要满足希尔伯特变换的约束关系,如果不满足,则信号占用的带宽仍然和双边带信号相同。
如果我们独立地设置正弦和余弦分量,虽然带宽仍然和双边带信号相同,但是传递的信息也增加了 一 倍,频谱效率和单边带信号是相同的,而且省掉了希尔伯特变换这个环节。
假设 I 路的信号为 \({x_I}\left( t \right)\),Q 路信号为 \({x_Q}\left( t \right)\),则经过 IQ 调制后的信号为:
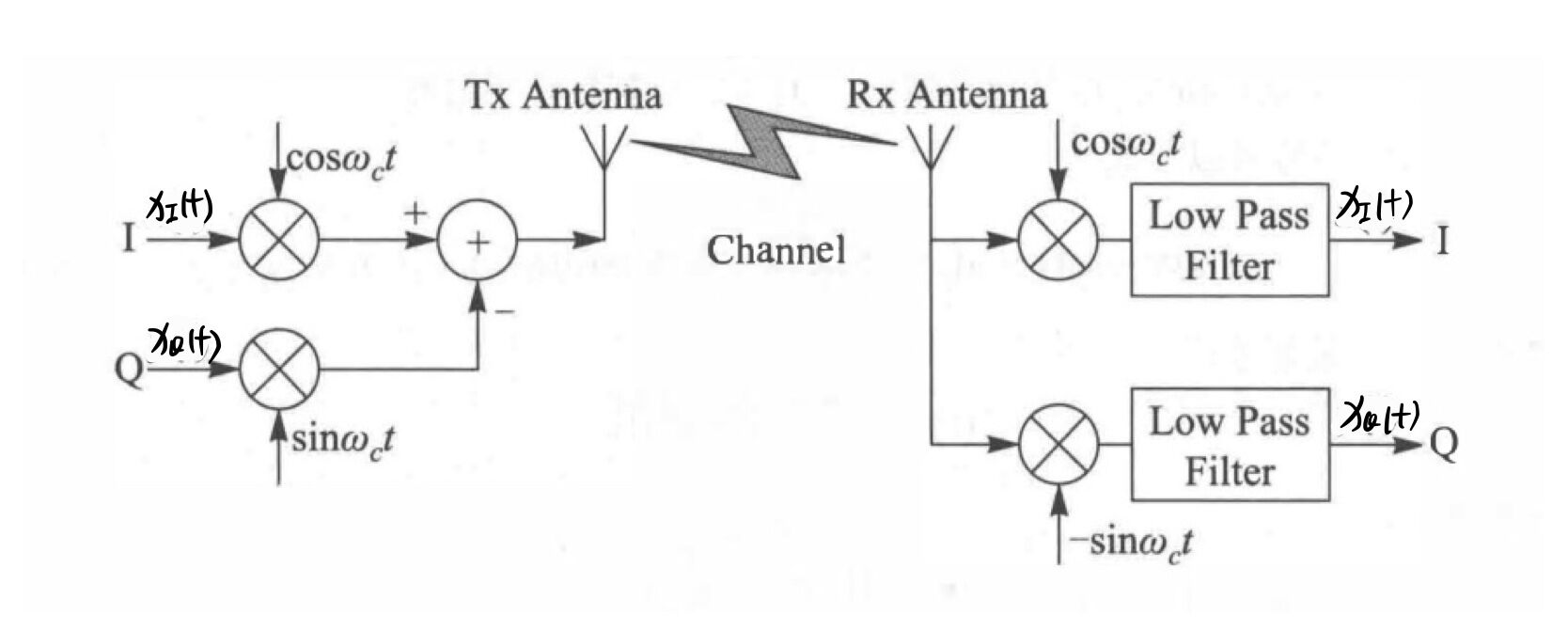
在下一节中可以得到复数信号 \(\left[ {{x_I}\left( t \right) + j{x_Q}\left( t \right)} \right]{e^{j{w_c}t}}\) 与实数信号 \({x_I}\left( t \right)\cos \left( {{\omega _c}t} \right) - {x_Q}\left( t \right)\sin \left( {{\omega _c}t} \right)\) 存在着一一对应的关系,为了表达的方便,我们经常把 IQ 信号看成是复数信号 [1:1]。自然界中的信号是实数,实数信号是实际的发射和接收过程,为了简化模型, 因此有了信号的复数表示。所以发送信号一般建模成:
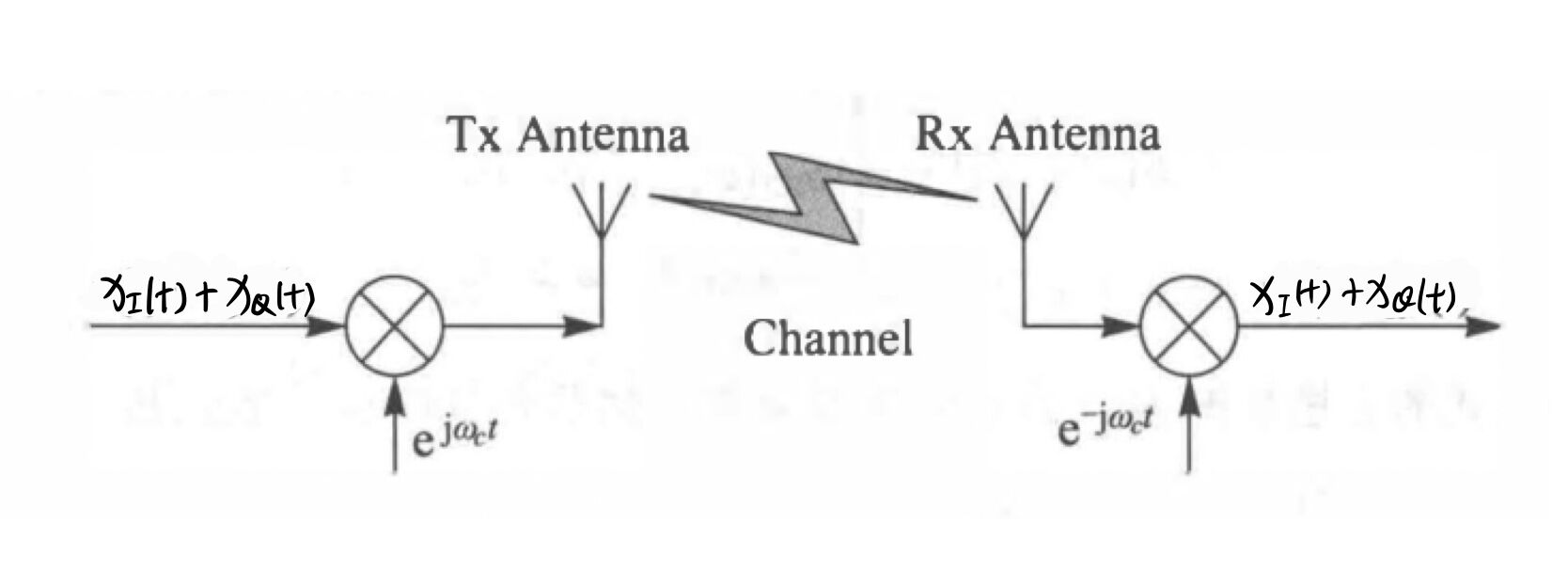
1.2 带通信号的复基带表示
如果信号带宽 B 远小于中心频率 \(f_c\),则信号 \(x\left( t \right)\) 称为带通信号,通信系统中的许多信号都是实带通信号。带通信号也可以由两个低通信号(的调制)来表示[2]:
\({x_I}\left( t \right)\) 称为 \(x\left( t \right)\) 的同相分量,\({x_Q}\left( t \right)\) 称为 \(x\left( t \right)\) 的正交分量。
定义复信号 \(u\left( t \right) = {x_I}\left( t \right) + j{x_Q}\left( t \right)\),我们可以得到:
由此可以看出,这个所得的复信号的实部其实就是带通信号,即:
这个复信号 \(u\left( t \right)\) 就称作是 \(x\left( t \right)\) 的等效基带信号或复包络,等式右边称为带通信号 \(x\left( t \right)\) 的复基带表示。
从信号与系统的学习中我们知道,一个信号 \(x\left( t \right)\) 通过系统,得到的信号时域上 \(y\left( t \right)\) 等于 \(x\left( t \right)\) 与系统的冲激响应 \(h\left( t \right)\) 的卷积。这在计算基带信号通过低通系统时运算方便,但是这对于带通信号和带通系统来说计算复杂。于是将信号经过等效处理,将复杂运算变为简单运算[3]。
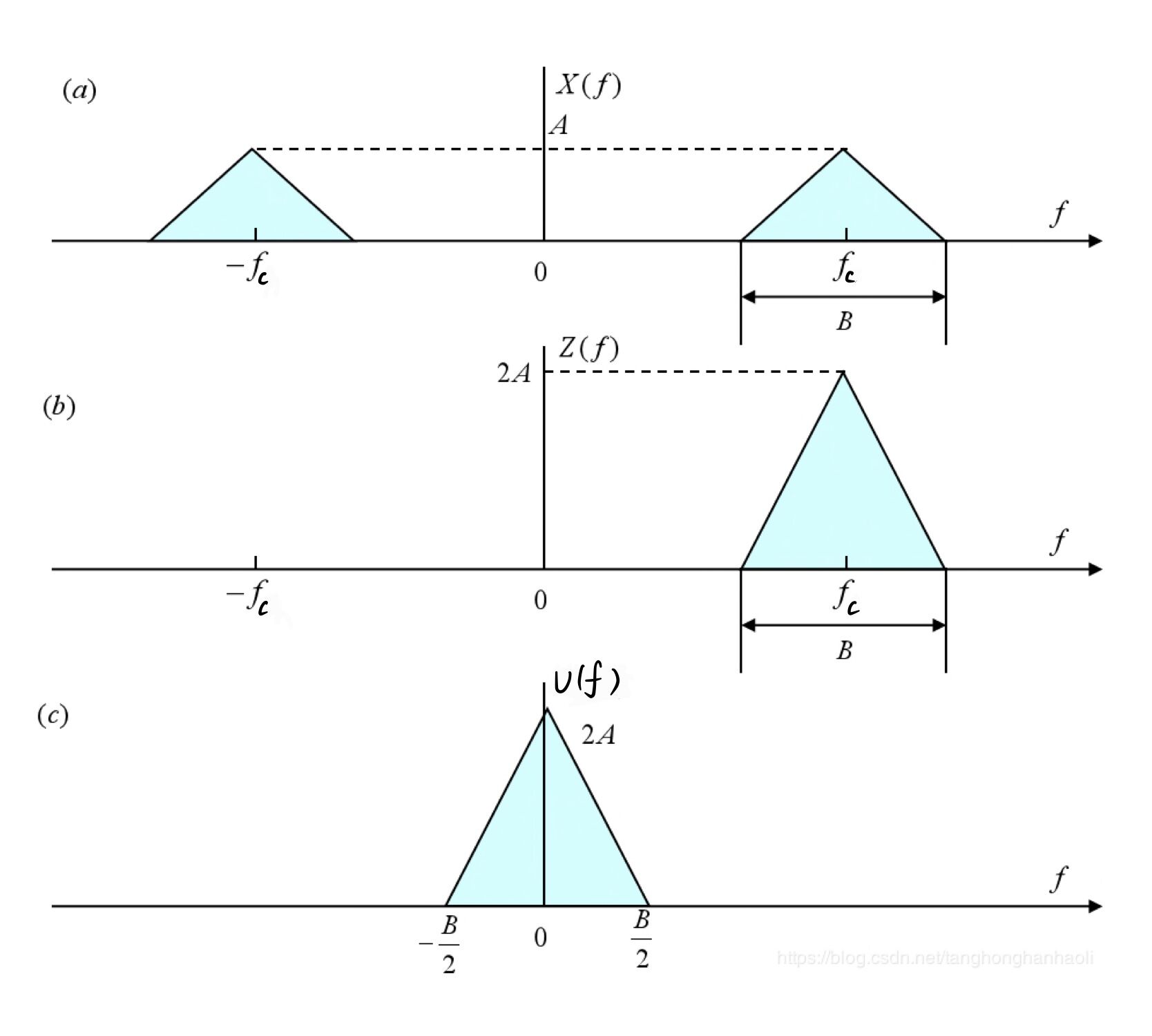
1.3 等效基带信号的频域图解
假设已知一个实带通信号为 \(x\left( t \right)\),其中心频率为 \(f_0\),带宽为 B,频谱示意图为 (a)。定义其解析信号 \(z\left( t \right)\) 为:
解析信号的实部为 \(x\left( t \right)\),虚部为 \(x\left( t \right)\) 的希尔伯特变换,其频谱示意图为 (b),正频率成分变为原来两倍,不再有负频率成分。解析信号本质上是原信号的正频谱部分,是实信号的一种“简练”形式[2:1]。
进一步,我们可知 \(x\left( t \right)\) 的复包络为 \(u\left( t \right) = {x_I}\left( t \right) + j{x_Q}\left( t \right)\),由于下式成立:
我们可知 \(u\left( t \right) = z\left( t \right){e^{ - j{w_c}t}}\),其复包络信号是将其频谱的中心点从 \(f_c\) 搬移到零频率处,这也是为什么称之为等效基带表示,或者说称 \(u\left( t \right)\) 为带通信号 \(x\left( t \right)\) 的低通表示[4]。