通信网实验—话务量分析

1 实验原理

通信业务量分析就是利用Relang B公式或C公式。确定业务量、中继线（或信道）数量和阻塞概率（或呼叫等待概率）之间的关系式。业务量理论就是用来设计在一定的服务等级上，能够处理一定呼叫容量的服务系统，目的是使固定数量的中继线路或信道可为一个数量更大的、随机的用户群体服务。

Erlang B公式也叫爱尔兰第一公式，应用于阻塞呼叫清除系统，该系统的排队模型为\(\rm{M/M/m(m)}\)。当用户呼叫时\(\rm{m}\)条线路均被占用时，新的呼叫直接被拒绝。Erlang B公式可表示为：

\[P_{c}=\frac{a^{m} / m !}{\sum\limits_{k=0}^{m} a^{k} / k !} \]

Erlang C公式也叫爱尔兰第二公式，应用于阻塞呼叫延迟系统，该系统的排队模型为\(\rm{M/M/m}\)。这个与Erlang B公式不同的是，当线路均被占用时新的呼叫不是直接被拒绝，该服务系统用一个队列缓冲来保存阻塞呼叫，如果不能直接获得一个信道，呼叫请求就一直延迟一段时间，直到有空闲信道或者被拒绝接续。Erlang C公式可以表示为：

\[ P_{c}=\frac{a^{m}}{a^{m}+m !\left(1-\frac{a}{m}\right) \sum\limits_{k=0}^{m-1} \frac{a^{k}}{k !}} \]

2 仿真结果

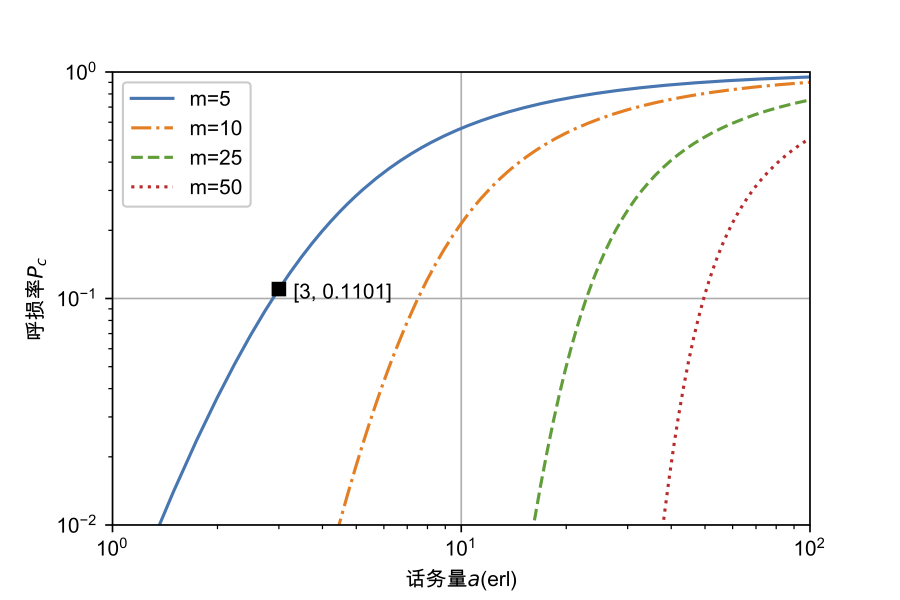
通过给定的信道数\(m\)，以及话务量\(a\)，绘制出呼损率\(P_c\)的变化曲线，Erlang B公式仿真曲线如图1所示：

3 代码

# Erlang B
from math import factorial
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import numpy as np
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']

def Erlang_B(a, m):
      sum = 0.0
      for k in range(m+1):
            sum += a**k/(factorial(k))
		
      return a**m/(factorial(m) * sum)
	
# 生成话务量
a = np.linspace(1, 100, 400)

p_m5 = []
p_m10 = []
p_m25 = []
p_m50 = []

for a0 in a:
      p_m5.append(Erlang_B(a0, 5))
      p_m10.append(Erlang_B(a0, 10))
      p_m25.append(Erlang_B(a0, 25))
      p_m50.append(Erlang_B(a0, 50))


# loglog绘图：https://www.bilibili.com/read/cv4194543
plt.loglog(a, p_m5)
plt.loglog(a, p_m10, '-.')
plt.loglog(a, p_m25, '--')
plt.loglog(a, p_m50, ':')
plt.legend(['m=5', 'm=10', 'm=25', 'm=50'])
plt.ylim(10e-3, 1)
plt.xlim(1, 100)

# 话务量为3, m=5时
plt.plot(3, Erlang_B(3, 5), 'ks')
show_max='['+str(3)+', '+str(round(Erlang_B(3, 5), 4))+']'
plt.annotate(show_max,xy=(3.3, 0.1))

plt.xlabel(r'话务量$a$(erl)')
plt.ylabel(r'呼损率$P_c$')
plt.grid()
plt.savefig('fig_1.eps')
plt.show()