Performance Scaling Laws

 

 

并行优化有两个 scaling laws指导优化的界。

Amdahl's Law

Amdahl's Law又叫strong scaling law。

Amdahl's Law
For a given workload in single node, the theoretical speedup of the latency of the workload, is constricted both by the number of processors executing and the serial proportion of the workload.

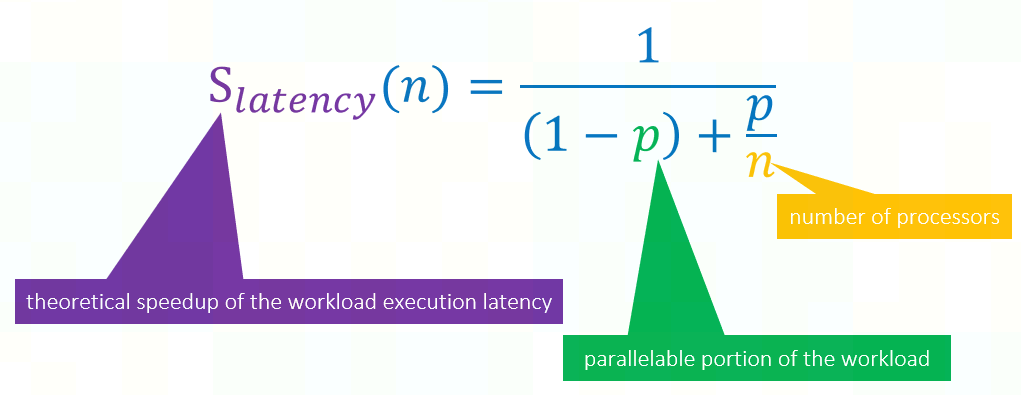
阿姆达尔定律解决的问题是：给定workload，优化其性能，关注于把给定的任务做好。
假设给定workload的初始latency为，其中可并行优化部分latency为, 非可并行优化部分latency为。
那么，使用n路并行只能优化其并行部分，优化后可并行部分最好latency为，非可并行优化部分latency仍为，总latency为。
因此，性能提升上限为, 即为。

Amdahl's Law是面向工程师的，提醒工程师谨防无用功，在性能优化时，除了看模块性能增益外，更要关注模块对整个workload的增益。在优化前一定要做好收益分析，而收益分析的前提是性能分布。
举个例子：一个可并行优化部分latency占总workload latency比为50%的workload。不管可并行部分怎么优化，它对这个workload的贡献上限为2x；且在模块性能已到8x优化后，对改部分的优化的投入的收益会很marginal，可以考虑多分析分析其他部分。

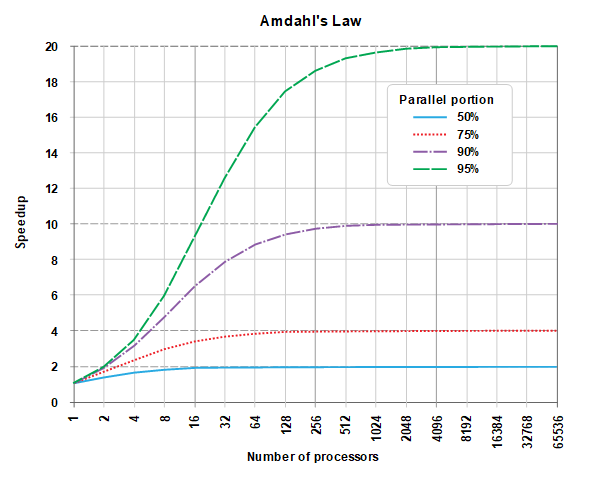
Amdahl's Law告诉我们对给定workload的优化是有明显饱和区的，因此要格外关注性价比指标。如何关注性价比指标，就是要做好测量，无测量不优化。对程序员来说就是执行好profiling based optimization。

Gustafson's Law

Gustafson's Law又叫weak scaling law。

Gustafson's Law
For a scaled-up/scaled-out workload in 𝑛 nodes, the theoretical speedup of the latency of the workload, is constricted both by the number of processors executing and the serial proportion of the workload.

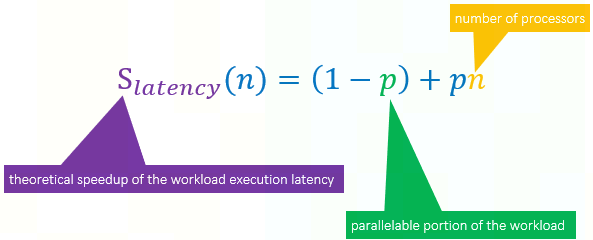
古斯塔夫森定律解决的问题是：做什么事情才能体现系统的能力，关注于做正确的事。
它把一个可在𝑛个nodes里运行的大规模workload的latency设为，其中并行部分latency为, 非并行部分latency为。
那么，如果使用个node去运行这个workload的话，并行部分所需要的latency会变为，非并行部分latency认为，总latency为。
因此，性能提升为, 即为。

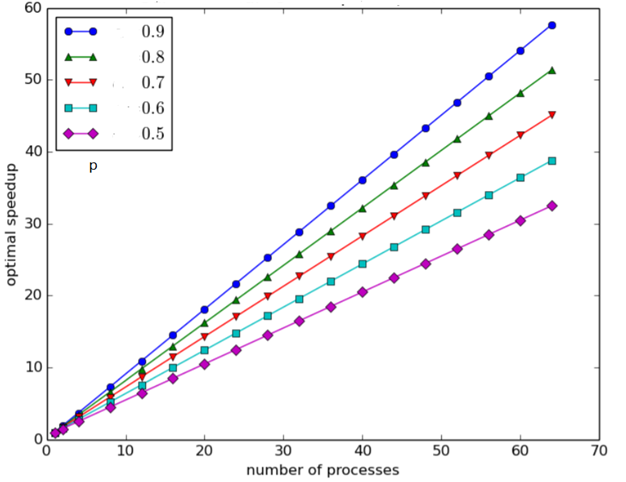
Gustafson's Law是面向决策者的，促使决策者思考在计算系统能力提高的时候除了考虑对现有应用场景(workload)好处外，更重要的是考虑新的能力会解锁哪些新应用场景(workload)。其隐藏的原因是：现有的workload一般在设计时是考虑了现有计算系统的承载能力的，因此在计算系统能力提高尤其是有质的提高时，对现有workload的优化都是服从Amdahl's Law，有可见的饱和区。而探索适配新的计算系统的workload，则服从Gustafson's Law，不管斜率如何，都有明显的线性区。
这也是在算力飞涨的如今，行业的前驱者(如Google，NV)不断寻找并启封以前的mission impossible workloads的内在驱动力。大规模模型训练，科学仿真(如分子动力学)等的蓬勃兴起就是题中之义。Amdahl's Law并不能给新计算系统的发展带来真正的原生需求，也就不能真正驱动算力的健康发展，只有Gustafson's Law才能。
同理可以看通信行业，困扰5G的不是网络优化等问题，而是需要解锁新的应用场景来justify它。