寻找模式之旅(1)_字符串匹配 之 确定性方法
— 寻找模式之旅
前言:科学家和工程师们一直试图从复杂的世界中找到简单的模式,从而通过研究简单的模式达到研究复杂事物的目的。正如我们“从乱草堆中找针”所做的一样,我们找的是那个“尖的银白色的硬的物体”,而这正是“针”的模式,因为它用得太多了,我们给这个模式起了个名字叫“针”,仅此而已。当然,这是我从我的角度给“针”编的一个出身故事,如果不对,还希望“针”兄不要见怪。J最近陆陆续续看了一些很杂的东西,总觉得渐渐地思想中隐出一条线来。我们做很多事情,其实是出于对简洁的模式的特殊癖好,出于对它给我们带来的兴奋的痴狂迷恋。所以,我想以“寻找模式之旅”为题,把我最近看的一些整理一下,也算是对自己的一个鞭策。这个系列的东西很杂,从字符串匹配,到素性判别,到分形,再到数据压缩。但它们有个共同的主线,那就是“模式”。
首先上场的是字符串匹配问题。分为三个文档:
Part 1:确定性方法。讨论基于逐个字符比对的方法,这跟我们刚开始学英语的时候辨认单词的方法一样,把这个单词与单词表或是心中记下来的那个单词的写法逐个字母比较,呵呵。主要的方法有基于前缀的方法,如著名的KMP算法,shift and/shift or算法;基于后缀的方法,主要介绍Horspool算法。
Part 2:随机化方法。讨论基于模式的算法,首先找到那些符合特定模式的子串,再对这些子串进行逐字符比对,这种由粗到精,多级过滤的方法是一种通用的系统架构,对于提高方案的性能很有效。
Part 3:正则表达式。
字符串匹配
-----确定性方法
我最初接触模式这个词就来自于字符串匹配,在很多教科书里把它叫做“模式匹配”。于是,我与“模式”就这样非正式地见面了。现在想来,把字符串匹配叫做“模式匹配”可能正是取的“在目标文本中找出含有给定字符串模式的文本段”之意吧。因为字符串匹配已经不再仅仅满足于找与给定字符串完全相同的文本段了,它也需要一写抵抗诸如拼写错误这类的能力,这就是所谓的“柔性字符串匹配”,其应用面应该更广了。这次我打算讨论的还仅仅是单字符串的精确匹配问题的确定性方法,主要讨论基于前缀的匹配算法和基于后缀的匹配算法两大类。
问题重述
字符串匹配问题有很广泛的用途:我们每天使用的windows中的文件查找或是word文档中的查找,都是字符串匹配问题的实现;我们能在搜索引擎上查找含有相应关键字的网页,也离不开字符串匹配;很多人做网络,在进行协议分析或是p2p流量整形的时候,字符串匹配算法时你发现目标的有力工具,就像生物学家的显微镜一样必不可少;提到生物学家,计算生物学家要在数以T计的数据找到带有一定模式的DNA序列,用眼睛肯定是不行的,还得使用字符串匹配算法…
除了这些直接的用途外,在解决字符串匹配问题中所提出的想法,怎么避免在不可能的子串上做无用功等等,对现在正如火如荼进行中的图像检索来说也是一笔值得借鉴的经验。
算法分析
一、基于前缀搜索的方法
所谓前缀搜索就是在搜索窗口沿着文本的读入顺序从前到后逐个读入文本字符,搜索窗口中文本,使其是模式串的最长公共前缀。
假设已经知道读入直到文本位置i的所有字符,并且已知既是已读入文本的后缀也是模式串P的前缀的最长字符串的长度,当该长度等于模式串P的长度时,就产生一个成功匹配。现在要解决的问题是:当读入下一个文本字符时,如何快速更新匹配长度。有两条思路:
ü 第一种思路直面问题,找到一种有效的机制来计算既是已读入文本的后缀也是模式串P的前缀的最长字符串。Knuth、Morris、Pratt找到了这种方法,即是我们所熟知的KMP算法。
ü 第二种思路就是维护一个集合,它包含了所有既是已读入文本的后缀也是模式串P的前缀的字符串,并且每读入一个文本字符时就更新该集合。当模式串的长度小于机器内基本类型的字长时,我们可以使用位图来维护这个集合,从而使用位并行方法来加速算法。这就是将要讨论的Shift-And/Shift-Or算法。
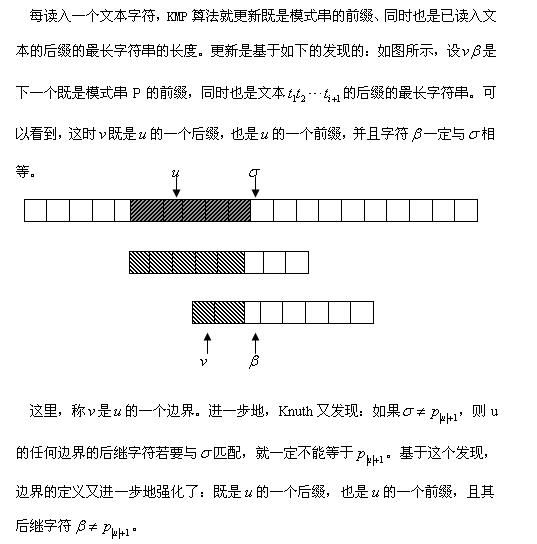
1.1 KMP算法
到这里,基本算法思路就出来了:

依惯例给出KMP的实现代码(C语言)。
1.2 Shift-And/Shift-Or算法
Shift-And/Shift-Or算法的想法很简单,它不想花很大的脑筋去想每次应该怎么更新最长前缀,索性每次都把既是模式串的前缀又是读入文本的后缀的字符串一股脑地保存到一个集合里,再根据新来的字符更新这个集合就行了。虽然更新集合可比更新最大前缀不费脑子多了;可是费时间,因为集合中的元素需要一个一个更新。有没有什么办法不这么费时间呢?有的!如果模式串的长度不超过32的话,我们可以使用位图来表示这个集合,到时候用位并行,一次就把一个集合更新完了,真所谓“条条大路通罗马”。

下面先给出Shift-And算法的代码。
从实现的角度来看,算法是不是可以更简单呢?这就是Shift-Or由此产生的原因。Shift-Or算法主要通过对位取反消除了更新公式中,从而加速了D的更新。各位可以想想为什么用反码就可以消除
呢?呵呵。
下面给出Shift-Or算法的实现代码。
二、 基于后缀搜索的方法
如果说基于前缀搜索的算法是搜索已读入文本中是否含有模式串的前缀的话,那么后缀搜索的意思也就很明显了,所谓后缀搜索也就是搜索已读入文本中是否含有模式串的后缀;如果有,是多长,显然,当后缀长度等于模式串的长度时,我们就找到了一个匹配。
基于后缀搜索的方法中最著名的其实是1977年提出的Boyer-Moore(简称BM)算法了。但是,它移动时需要计算三个距离,并在其中选择出最大的安全滑动距离来滑动模式串。算法比较复杂,而且时间性能并未如理论研究所显示的那样好。1980年Horspool做出了一个大胆的假设,他认为:对于较大的字母表来说,首先满足模式串最后一个字符的匹配性总是能产生最大的安全滑动距离。从此,出现了Horspool算法。
Horspool算法认为:对于每个文本搜索窗口,将窗口内的最后一个字符()与模式串的最后一个字符进行比较。如果相等,则继续从后向前验证其他字符,直到完全相等或者某个字符不匹配。然后,无论匹配与否,都将根据
在模式串的下一个出现位置将窗口向右移动。
下面给出Horspool算法的源代码。
总结
在确定性算法中,理论分析认为KMP算法的最坏时间复杂度是线性的,线性时间复杂度被认为是所有串匹配算法的最坏时间复杂度的下界,因而KMP算法被认为是最优的算法。但是事实却并非如此,Gonzalo Navarro指出:在字符串匹配领域有两个典型的例子,一是著名的KMP算法,它在实际应用中比简单的蛮力算法还要慢一倍。二是在著名的BM系列算法中,应用最成功的算法是对原始算法进行高度简化后得到的算法(即Horspool算法)。
我想这是我们最应该从中获得教训的地方,理论的美妙需要落到实际的应用中去检验。
最后给出上述算法的性能结论:
(1) 当模式串长度小于8时,KMP算法才比基于后缀和基于子串的搜索方法有效。而在这个范围内,Shift And/Shift Or算法能够在所有机器上运行,速度至少是KMP算法的两倍,并易于实现。
(2) 随着字母表的增大,Horspool算法越来越占据绝对优势。
另外,本文没有给出基于子串的匹配算法的研究,包括BOM、BNDM算法,是串匹配中理论与实践结合的典范,但本人还没有进行过学习。
参考文献
【1】 Gonzalo Navarro etc. Flexible Pattern Matching in Strings