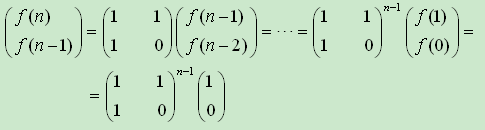Fibonacci数的生成

 

   Fibonacci数被称为“黄金分割数”，因为其相邻两项的比值越来越趋近黄金分割比例。据说是进制数的先驱的Fibonacci频繁被人们提起却是由于其在《算盘书》中提出的“兔子繁殖”问题：

如果一对兔子每月能生一对小兔（一雄一雌），而每对小兔在它出生后的第三个月里，又能开始生一对小兔，假定在不发生死亡的情况下，由一对出生的小兔开始，50个月后会有多少对兔子？

   Fibonacci可能没想到的是，这道题目最后成就了他，从此他的名字永远留在了数学史和计算机史上。由这道题引发的一个数列被人们称为Fibonacci数列。

   那么什么是Fibonacci数列呢？它的定义如下：

 一个数列被称为Fibonacci数列，当他满足如下条件：

                 f(n)= 0 ,n = 0

                 f(n)= 1, n = 1

                 f(n)= f(n-1)+f(n-2),其它

 我们现在要讨论的问题就是，如何计算第n项Fibonacci数的值呢？下面我们就开始讨论几种不同的方法。

方法一、递归法（从后往前推）

   想要知道f(n)，知道f(n-1)和f(n-2),f(n)就好办了，因为f(n) = f(n-1)+f(n-2)，而f(n-1)、f(n-2)又可以表示成其前两项的和，直到n = 0,1为止。这样，一个问题被分解成很多个相同形式的子问题。只要解决了这些子问题，那么最初的问题自然就被解决了。这就是分治法的思路。

   自此，我们可以写一个递归的程序来解决这个问题：

 

#include <iostream>
#include "fibo.h"

using namespace std;

unsigned long fibo_recursion(int n)
{
   if(n < 0)
   {
     cout<<"error!"<<endl;
     cout<<"Please input a number that is larger than or equal to 0"<<endl;
     return 0UL;
   }
   else if(n == 0)
    {
      return 0UL;
    }
    else if(n == 1)
    {
      return 1UL;
    }
    else
      return (fibo_recursion(n-1) + fibo_recursion(n-2));
}

                                                                                                                     

我们可以看到，代码非常简洁，就是公式的翻版。但是只要执行过的人就会有深刻的体会，代码的效率是很低的。算一个f(40) 要14.75s，而f(50)6分钟还算不出来（Pentium4 2.8GHz,1.5G内存，WINDOWS XP）。现在，我们分析一下，为什么会这么慢呢？我们重走一下流程：

           

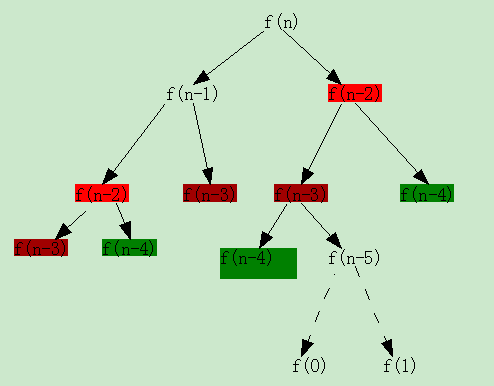
  我们发现，在分治的过程中，有很多的子问题被重复计算了，这种情况越往下走越严重。甚至，我们发现，某一项被重复计算的次数等于其后两项被重复计算的次数之和，还是Fibonacci数列！！！这种情况是不妙的，说明递归越深，重复计算的次数是随着深度的增加呈指数增长的态势的。这就解释了为什么f(40)14.75s能算出来，而f(50)6分钟还算不出来了。怎样避免重复计算呢。我们来看方法二。

方法二、递推法（从前往后推）

 不重复计算的方法就是，从前往后推。由f(0)、f(1) 算出f(2) ，依次类推，一直到f(n)。这样，每项只被计算一次。我们看下源码：

 

#include <iostream>

using namespace std;

unsigned long fibo_recurrence(int n)
{
  if(n < 0)
   {
     cout<<"error!"<<endl;
     cout<<"Please input a number that is larger than or equal to 0"<<endl;
     return 0UL;
   }
  else if(n == 0)
   {
     return 0UL;
   }
  else if(n == 1)
   {
     return 1UL; 
   }
  else
   {
     unsigned long nebor[2] = {0,1};
     int k = 2;
     int parity = 0;
     while(k<=n)
      {
         parity = (k & 1);
         nebor[parity] += nebor[1-parity]; 
         k++;
      }
     return (nebor[parity]); 
   }
}

 

这段程序比前一段多加了一个错误处理，这在程序设计的时候是应该考虑的。

现在我们跑一下f(50) ，时间是0s，也就是其运算时间在几十毫秒以内。

感觉递推法，已经不错了，是不是还有别的方法呢？有的！那就是：矩阵法。

方法三、矩阵法

矩阵法也是基于Fibonacci的定义。我们可以把Fibonacci数列的定义改写成以下形式：

   

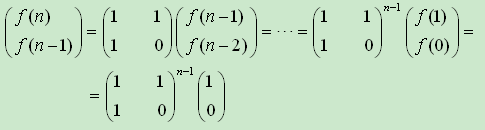
这样，我们发现计算f(n)就变成了矩阵的幂的计算。

 对于幂的计算也有相应的Horner法。下面给出源码：

 

#include <iostream>
#include <vector>

using namespace std;
typedef struct
{
    unsigned long a11;
    unsigned long a12;
    unsigned long a21;
    unsigned long a22;
}matrix;

inline matrix matrix_square(matrix a)
{
    matrix res = {0};

    res.a11 = a.a11*a.a11 + a.a12*a.a21;
    res.a12 = a.a11*a.a12 + a.a12*a.a22;
    res.a21 = a.a21*a.a11 + a.a22*a.a21;
    res.a22 = a.a21*a.a12 + a.a22*a.a22;
    
    return res; 
    
}


inline matrix matrix_multiply(matrix a,matrix b)
{
    matrix res = {0};
    
    res.a11 = a.a11*b.a11 + a.a12*b.a21;
    res.a12 = a.a11*b.a12 + a.a12*b.a22;
    res.a21 = a.a21*b.a11 + a.a22*b.a21;
    res.a22 = a.a21*b.a12 + a.a22*b.a22;
    
    return res; 
    
}

vector<unsigned> decTobin(int val, int n)
{
    vector<unsigned> coefs;
    int ppow = 1;
    int p = 2;
    for (int i = 0; i < n; i++)
    {
        coefs.push_back( (val % (p*ppow))/ppow );
        ppow *= p;
    }
    return coefs;
}

unsigned long fibo_matrix(int val)
{
     int val2 = val-1;
     if(val2 == 0)
     {
         return 0UL;
     }
     else if (val2 == 1)
     {
         return 1UL;
     }
     else
     {

         int n = 0;
        while(0 != val2)
        {
          n++;
          val2 = val2/2;
        }
        matrix result = {1,0,0,1};
        matrix begin = {1,1,1,0};
        vector<unsigned> bin(n);
        bin = decTobin(val-1,n);
        if (bin[0] == 1)
        {
            result.a12 = 1;
            result.a21 = 1;
            result.a22 = 0;
        }
        for (int i = 1;i<n;i++)
        {
            begin = matrix_square(begin);
            if (bin[i] != 0)
             {
               result = matrix_multiply(result,begin);  
             }
        }
        return (result.a11);
     }
}

       

结束本文。