已知向量\(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\)满足\(\left | \boldsymbol{a}\right |=2\),\(\boldsymbol{b}=\boldsymbol{a}\cdot\boldsymbol{b}=3\),\(\boldsymbol{c}=x\boldsymbol{a}+y\boldsymbol{b}\)\((x>0,y>0)\),若向量\(\boldsymbol{c}-2\boldsymbol{a}\)与向量\(\boldsymbol{c}-\dfrac{2}{3}\boldsymbol{b}\)的夹角为\(\dfrac{\pi}{3}\),则\(\left | \boldsymbol{c}-\dfrac{1}{2}\boldsymbol{a}\right|\)的取值范围是\((\qquad)\)
\(\mathrm{A}.\left[\sqrt{7}-2,\sqrt{7}+2\right]\) \(\qquad\mathrm{B}.\left( 3,\sqrt{7}+2\right]\) \(\qquad\mathrm{C}.[1,3)\) \(\qquad\mathrm{D}.\left(\sqrt{3},\sqrt{7}+2\right]\)}
解析:
由题易知\(\boldsymbol{b}=3\),且\(\boldsymbol{a},\boldsymbol{b}\)的夹角为\(\dfrac{\pi}{3}\),若记$$ \overrightarrow{OA}=\boldsymbol{a}, \overrightarrow{OB}=\boldsymbol{b}, \overrightarrow{OC}=\boldsymbol{c},$$如图所示.
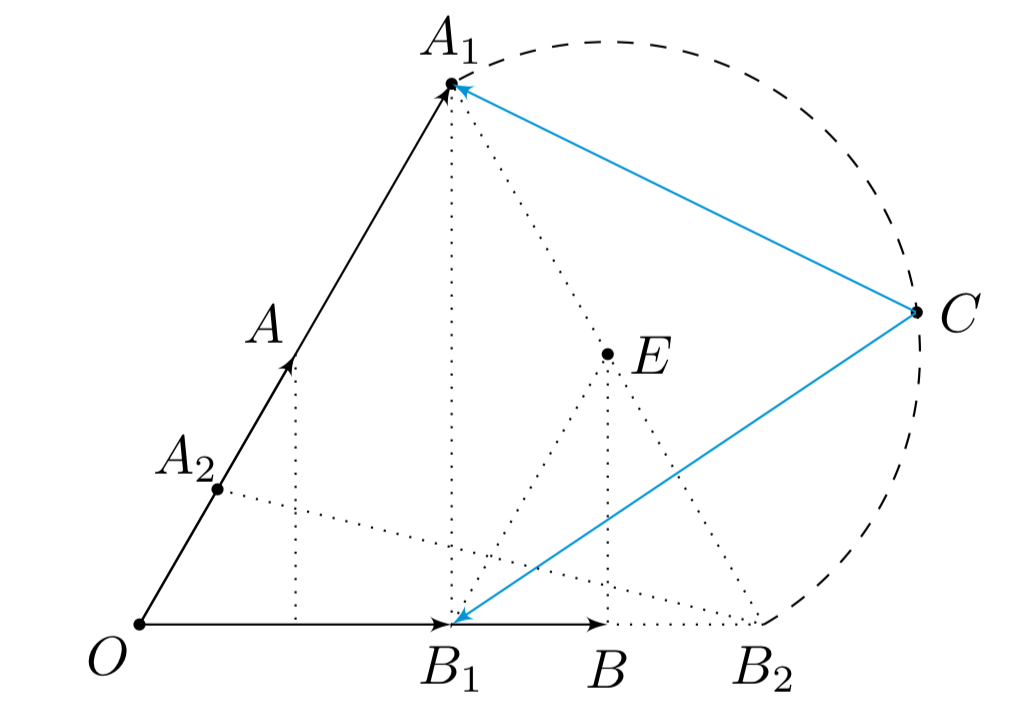
图中$$ \overrightarrow{OA}=\dfrac{1}{2} \overrightarrow{OA_1}=2 \overrightarrow{OA_2}, \overrightarrow{OB}=\dfrac{3}{2} \overrightarrow{OB_1}=\dfrac{3}{4} \overrightarrow{OB_2}.$$ 则由题可知 $$\left< \overrightarrow{CA_1}, \overrightarrow{CB_1}\right>=\dfrac{\pi}{3}.$$又因$C$点在角$\angle AOB$内部,因此点$C$的轨迹是以$A_1B_2$为直径的一段圆弧$($不含端点$)$.所以$$ 3=| \overrightarrow{A_2A_1}|<| \overrightarrow{CA_2}|=\left | \boldsymbol{c}-\dfrac{1}{2}\boldsymbol{a}\right|\leqslant |A_2E|+2=\sqrt{7}+2.$$ 所以$\left | \boldsymbol{c}-\dfrac{1}{2}\boldsymbol{a}\right|$的取值范围为$\left( 3,\sqrt{7}+2\right]$.