已知正方形\(ABCD\)的边长为\(7\),点\(M,N\)分别在\(AB,BC\)上,且\(AM=BN=3\),现有一束光线从点\(M\)射向点\(N\),光线每次碰到正方形的边时反射,则这束光线从第一次回到\(M\)时所走过的路程为\((\qquad)\)
\(\mathrm{A}.40\sqrt{5}\) \(\qquad\mathrm{B}.60\) \(\qquad\mathrm{C}.60\sqrt{5}\) \(\qquad\mathrm{D}.70\)}
解析
如图所示,将边\(AD\)关于\(BC\)对称得到\(A_1D_1\),将\(BC\)关于\(A_1D_1\)对称得到\(B_1C_1\),
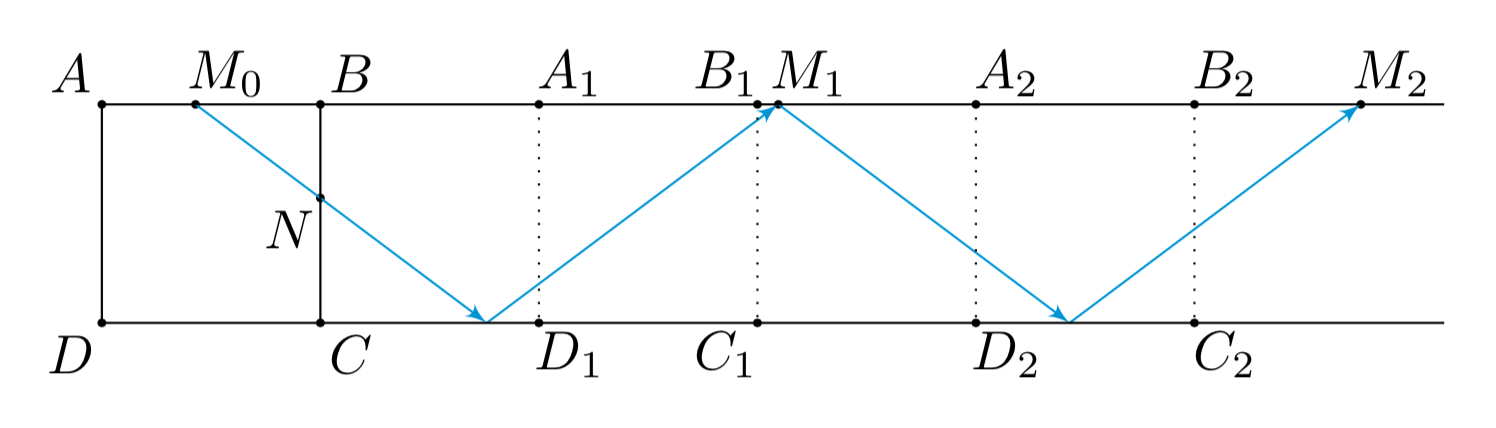
依此类推.则光线第$k$次回到边$AB$上时,在水平方向走过的路程为$$|M_0M_k|=k\cdot 2\cdot 7\cdot \dfrac{4}{3}=\dfrac{56k}{3},k=1,2,3,\cdots.$$ 由于在直线$AB$上任意两个相邻的$M$点的间距为$8$或$6$,所以当$M_k$与$M_0$重合时,有两种可能. 情形一 若 $$ \begin{split} &|M_0M_k|=(4+4+3+3)\cdot (n-1)+(4+4)\\ \Longleftrightarrow &56k=42(n-1)+24\\ &n\in\mathbb{N}^\ast. \end{split} $$ 由于$$ LHS \neq RHS\pmod{7}.$$ 所以该种情形不可能. 情形二 若$$|M_0M_k|=(4+4+3+3)\cdot n\Leftrightarrow 56k=42n,n\in\mathbb{N}^\ast. $$所以$k=\dfrac{3}{4}n$,当$n=4$时,$k$取得最小值,相应的$\left|M_0M_k\right|$也取得最小值$56$,光线走过的实际最短路程为$$ \dfrac{5}{4}\cdot\left| M_0M_k\right|=70.$$