已知正方体\(ABCD-A_1B_1C_1D_1\)的棱长为\(\sqrt2\),点\(P\)为对角线\(A_1C_1\)的中点,\(E,F\)分别为对角线\(A_1D\),\(BC_1(\)含端点\()\)上的动点,则\(PE+PF\)的最小值为\((\qquad)\)
\(\mathrm{A}.\sqrt{2}\) \(\qquad\mathrm{B}.\sqrt{3}\) \(\qquad\mathrm{C}.2\) \(\qquad\mathrm{D}.2\sqrt{2}\)
解析 如图所示,将正方体\(ABCD-A_1B_1C_1D_1\)关于平面\(A_1B_1C_1D_1\)对称得到正方体\(A'B'C'D'-A_1B_1C_1D_1\),则$$
PE+PF=PE'+PF.$$显然\(A_1D'\)和\(BC_1\)平行,因此当\(E',P,F\)三点共线并且\(E'F\perp BC_1\)时,所求表达式取得最小值.
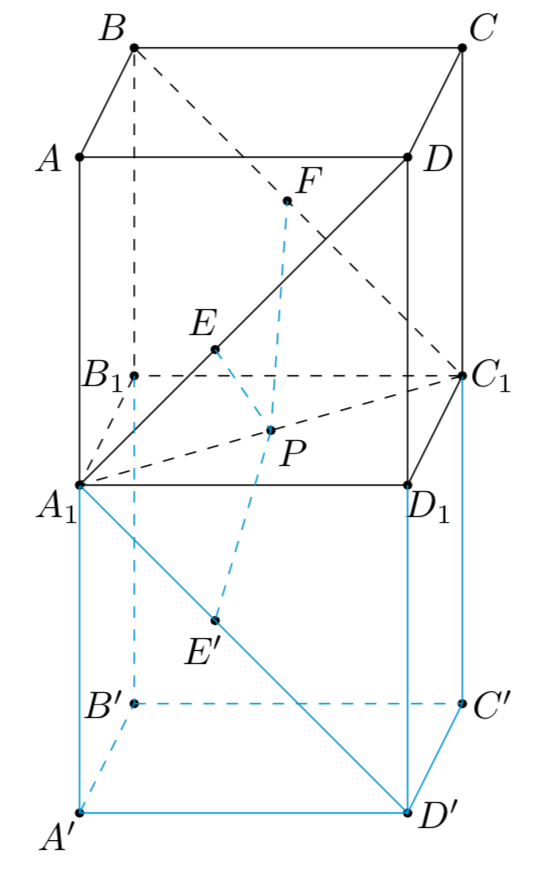
即求$A_1$到$BC_1$的距离,而$\triangle A_1BC_1$为正三角形,所以$A_1$到$BC_1$的最小值为$\sqrt{3}$.因此正确选项为$\rm B$.