设\(F_1,F_2\)是椭圆\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)\)的左右焦点,点\(P\)在椭圆上, 且\(\angle F_1PF_2=\dfrac{\pi}{3}\), \(\triangle F_1PF_2\)的外接圆的半径与其内切圆半径之比为\(2:1\).
\((1)\) 求椭圆的离心率\(e\);
\((2)\) 设\(AB\)是椭圆垂直于\(x\)轴的弦,\(C\)的坐标为\((3,0)\),直线\(BC\)与椭圆交于点\(E\),若直线\(AE\)恒过定点\(\left(\dfrac{4}{3},0\right)\),求椭圆的方程.
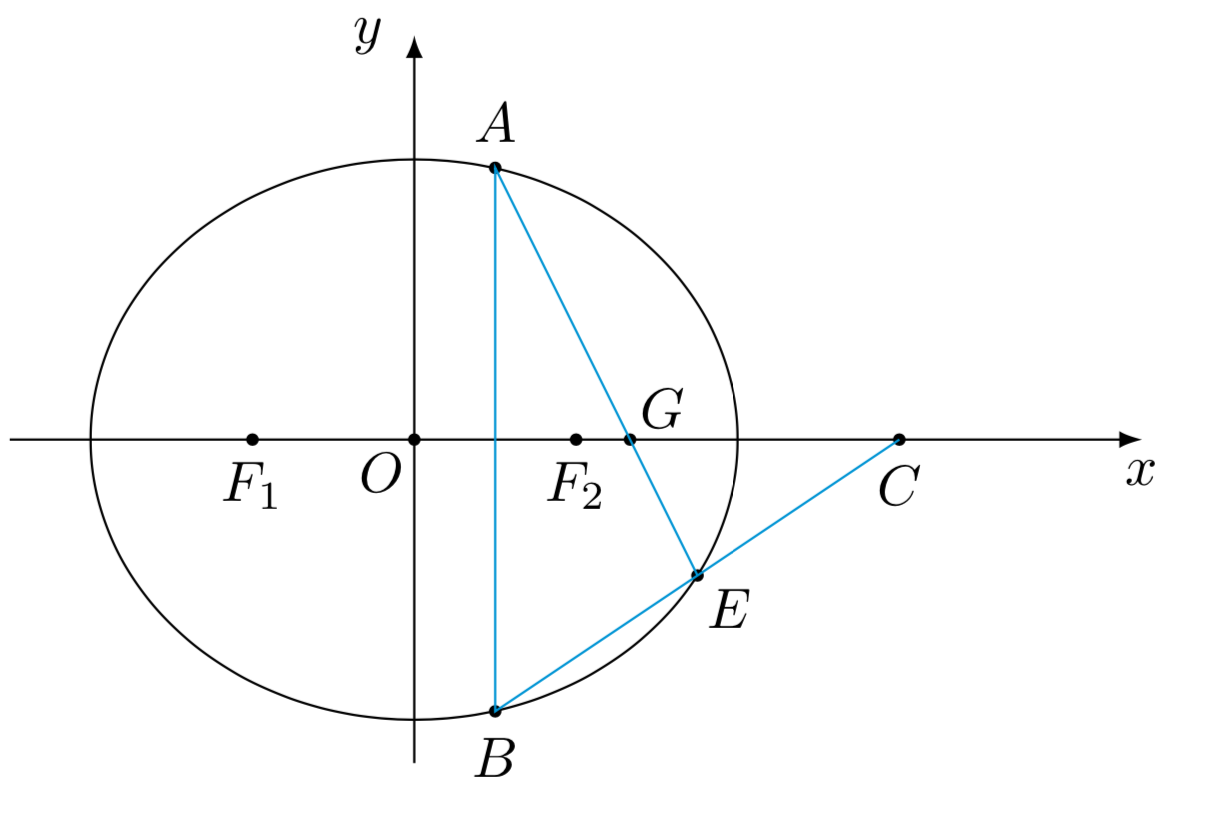
解析: $(1)$ 设$\triangle F_1PF_2$的外接圆和内切圆半径分别为$R,r$,设$c$为椭圆的半焦距,则由正弦定理可知$$ R=\dfrac{1}{2}\cdot \dfrac{|F_1F_2|}{\sin \angle F_1PF_2}=\dfrac{2\sqrt{3}c}{3}.$$ 由椭圆焦点三角形面积公式可知,$\triangle F_1PF_2$的面积$$ S_{\triangle F_1PF_2}=b^2\tan\dfrac{\angle F_1PF_2}{2}=\dfrac{\sqrt{3}}{3}b^2=\dfrac{\sqrt{3}}{3}(a^2-c^2).$$ 易知$\triangle F_1PF_2$的周长为$$ L_{\triangle F_1PF_2}=|PF_1|+|PF_2|+|F_1F_2|=2(a+c).$$ 由等面积法计算得$\triangle F_1PF_2$的内切圆半径长为$$ r=\dfrac{2S_{\triangle F_1PF_2}}{L_{\triangle F_1PF_2}}=\dfrac{\sqrt{3}}{3}\left(a-c\right).$$又由$R:r=2:1$可得$$ e=\dfrac{c}{a}=\dfrac 12.$$ $(2)$ 法一 如图,连接$AC$,由于$A,B$关于$x$轴对称,因此直线$BC$和$AC$也关于直线$x$轴对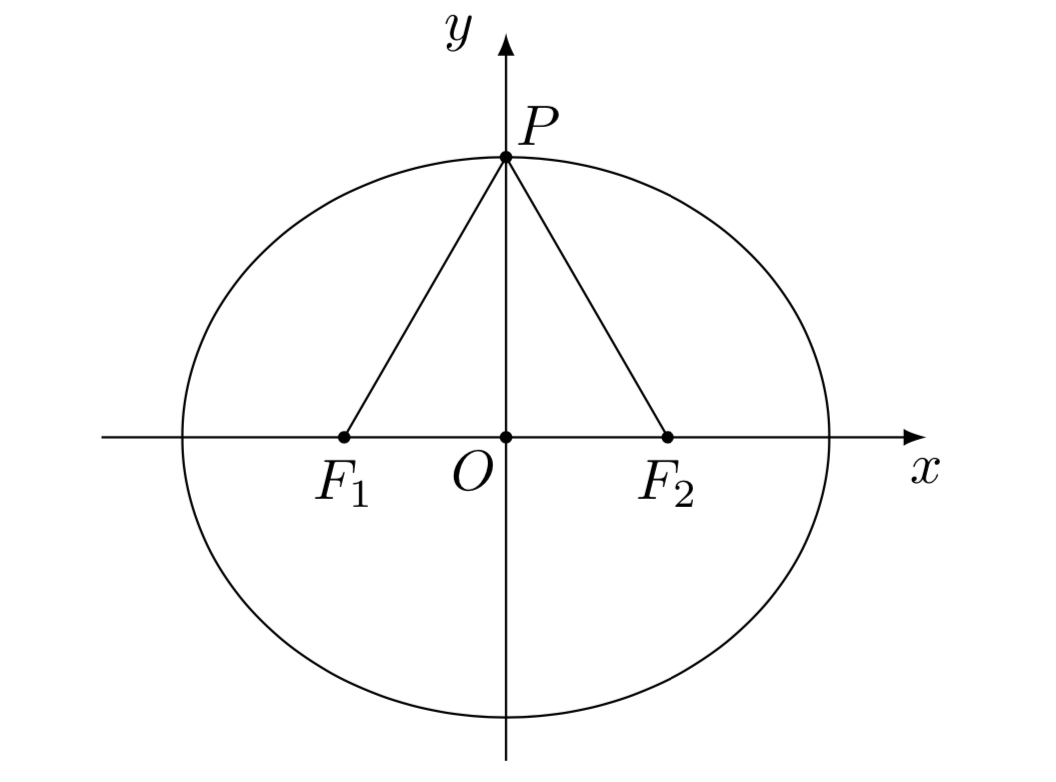
称,从而$AC$与椭圆的另一个交点$M$也与$E$关于$x$轴对称,所以$M,G,B$三点共线.其中$G$的坐标为$$G\left(\dfrac{4}{3},0\right),$$ 结合$(1)$可设椭圆方程为$\dfrac{x^2}{4t}+\dfrac{y^2}{3t}=1$,其中$t>0$.则$C$点位于$G$点关于椭圆的极线$$x=3t$$上.而$C(3,0)$,所以$t=1$,于是可得所求椭圆方程为$\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$. 法二
设待求椭圆方程为$\dfrac{x^2}{4t^2}+\dfrac{y^2}{3t^2}=1$,其中$t>0$,则$A,B,E$三点坐标可记为 $$ \begin{split} &A\left(2t\cos\alpha,-\sqrt{3}t\sin\alpha\right) ,\\ &B\left(2t\cos\alpha,\sqrt{3}t\sin\alpha\right),\\ &E\left(2t\cos\beta,\sqrt{3}t\sin\beta\right). \end{split} $$ 由于$BE$直线的$x$截距为$3$,因此由截距坐标公式可得 $$ \begin{split} 3&=\dfrac{2t\cos\alpha\cdot \sqrt{3}t\sin\beta-2t\cos\beta\cdot\sqrt{3}t\sin\alpha}{\sqrt{3}t\sin\beta-\sqrt{3}t\sin\alpha}\\ &=\dfrac{2t\sin\left(\beta-\alpha\right)}{\sin\beta-\sin\alpha}\\ &=\dfrac{2t\cos\dfrac{\beta-\alpha}{2}}{\cos\dfrac{\beta+\alpha}{2}}. \end{split} $$ 同理,由直线$AE$的$x$截距为$\dfrac{4}{3}$,可得$$ \dfrac{4}{3}=\dfrac{2t\cos\dfrac{\beta+\alpha}{2}}{\cos\dfrac{\beta-\alpha}{2}}.$$将以上两式相乘可得$ 4=4t^2$,从而解得 $t=1$ ,于是所求椭圆方程为 $\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$.
