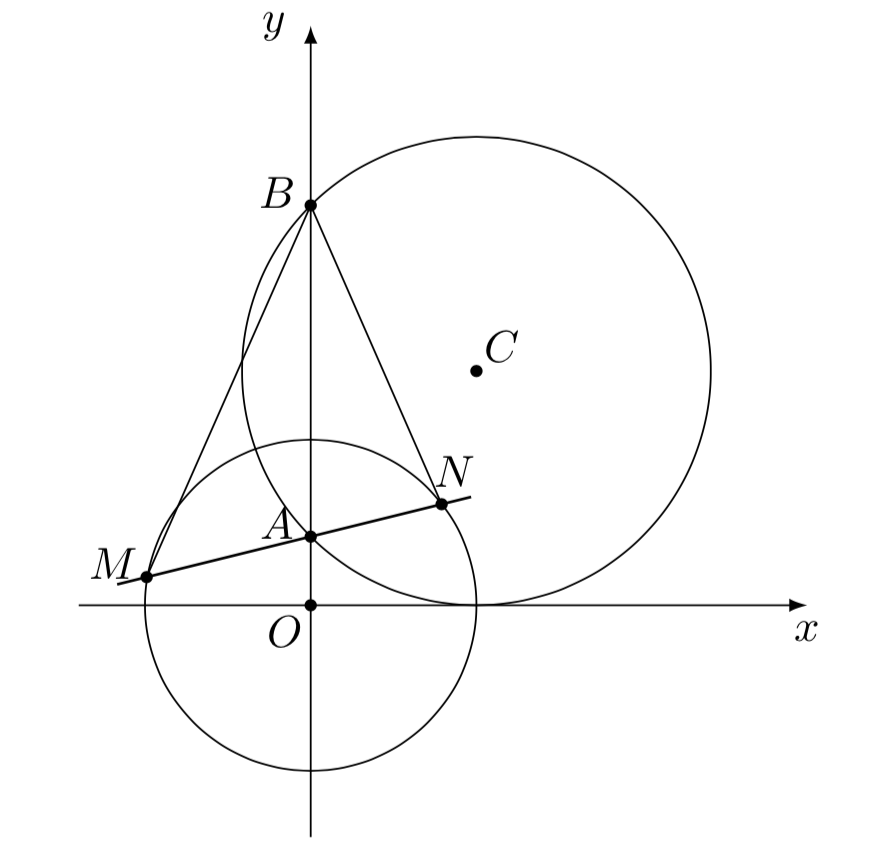
\((15\text{年湖北卷理科})\) 如图,圆\(C\)与\(x\)轴相切于点\(T(1,0)\),与\(y\)轴正半轴交于两点\(A,B(B\)在\(A\)的上方\()\),且\(|AB|=2\).
\((1)\) 圆\(C\)的标准方程为\(\underline{\qquad\qquad}\);
\((2)\) 过点\(A\)任作一条直线与圆\(O:x^2+y^2=1\)相交于\(M,N\)两点,下列三个结论:
① \(\dfrac{|NA|}{|NB|}=\dfrac{|MA|}{|MB|};\)
② \(\dfrac{|NB|}{|NA|}-\dfrac{|MA|}{|MB|}=2;\)
③ \(\dfrac{|NB|}{|NA|}+\dfrac{|MA|}{|MB|}=2\sqrt{2};\)
其中正确结论的序号是\underline{\qquad\qquad}(写出所有正确结论的序号).
解析:
\((1)\) 由题可设圆\(C\)的标准方程为$$
(x-1)2+(y-b)2=b^2,b>0.$$
取\(AB\)中点\(E\),连接\(EC\),\(AC\)
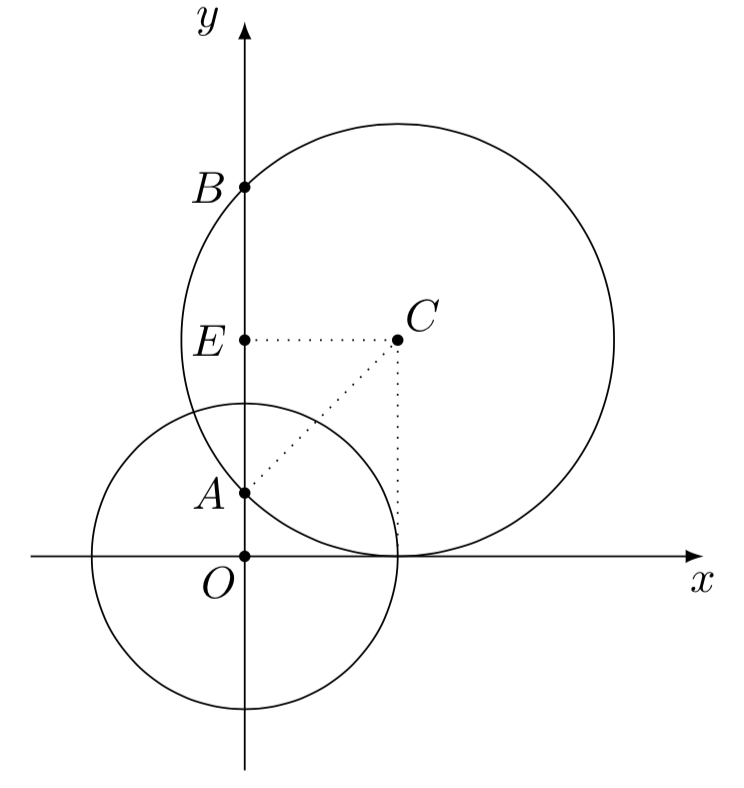
则有$$ 1^2+1^2=|EC|^2+|EA|^2=|AC|^2=b^2.$$所以$b=\sqrt2$.因此所求圆$C$的方程为$$(x-1)^2+(y-\sqrt{2})^2=2.$$ $(2)$ 法一 结合$(1)$可知$A(0,\sqrt{2}-1)$,$B(0,\sqrt{2}+1)$,设$N(\cos\theta,\sin\theta)$,则 $$ \begin{split} \dfrac{|NA|}{|NB|} =&\sqrt{\dfrac{\cos^2\theta+\left(\sin\theta-\sqrt{2}+1\right)^2}{\cos^2\theta+\left(\sin\theta-\sqrt{2}-1\right)^2}}\\ =&\sqrt{ \dfrac{\left(\sqrt{2}-\sin\theta\right)(\sqrt{2}-1)}{(\sqrt{2}-\sin\theta)(\sqrt{2}+1)}}\\ =&\sqrt{3-2\sqrt{2}}=\sqrt{2}-1. \end{split} $$ 同理可得$$ \dfrac{|MA|}{|MB|}=\sqrt{2}-1.$$因此结论 ①②③ 均正确. 法二 结合阿波罗尼斯圆的知识可知$A,B$两点是关于圆$O$的一对反演点,且有 $$\dfrac{|NA|}{|NB|}=\dfrac{|MA|}{|MB|}=\sqrt{2}-1.$$因此结论 ①②③ 均正确. 法三 结合$(1)$可知$A(0,\sqrt{2}-1)$,$B(0,\sqrt{2}+1)$.如图,连接$OM,ON$,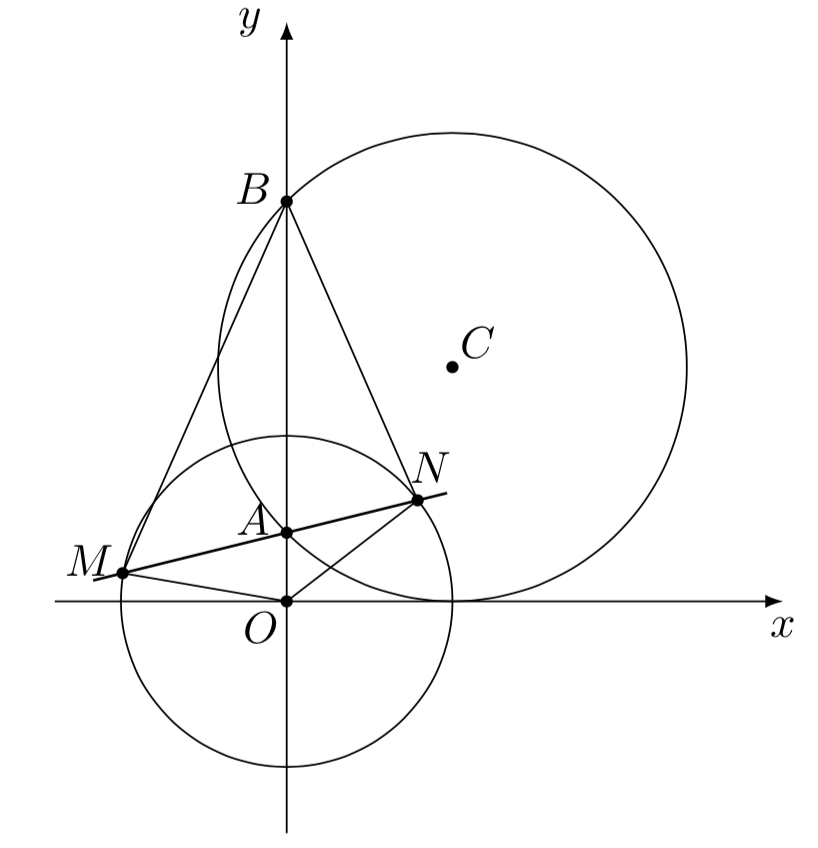
由于$$\dfrac{|OA|}{|ON|}=\dfrac{|ON|}{|OB|}=\sqrt{2}-1.$$因此 $\triangle OAN\sim \triangle ONB $ ,于是$$ \angle OBN=\angle ONA=\angle OMA.$$于是 $\triangle ABN\sim \angle AMO$ ,所以$$ \dfrac{|NA|}{|NB|}=\dfrac{|OA|}{|OM|}=\sqrt{2}-1.$$ 因此结论 ①②③ 均正确.