如图,三棱锥\(A-BCD\)中,\(AC=AD=BC=BD=10\),\(AB=8\),\(CD=12\),点\(P\)在侧面\(ACD\)上,且到直线\(AB\)的距离为\(\sqrt{21}\),则\(PB\)的最大值是\(\underline{\qquad\qquad}\).
解析: 由题,到直线$AB$距离等于$\sqrt{21}$的点构成的集合是一个圆柱面.这个圆柱面与$\triangle ACD$相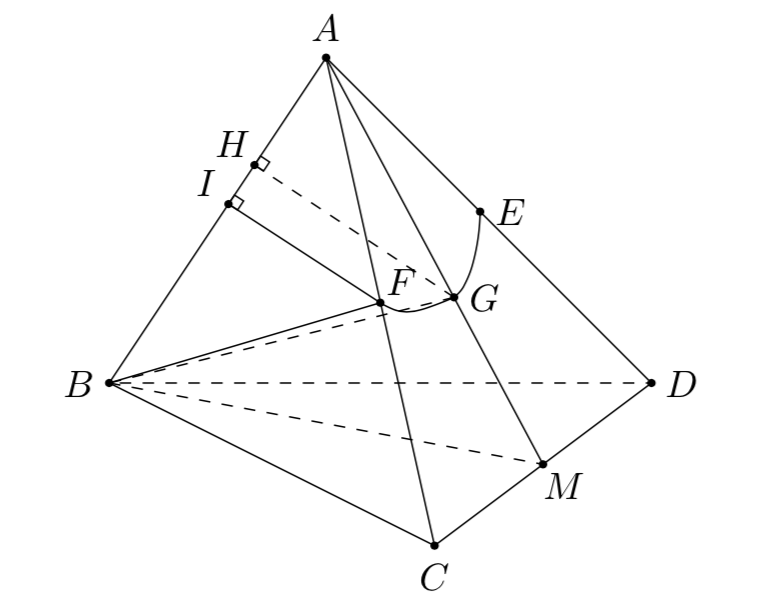
交所得为一椭圆.如图曲线$EGF$为该椭圆上一段,因此当$P$在曲线$EGF$运动时,始终满足题意,于是转求$BP$长度的最大值. 易知曲线$EGF$关于$AM$对称,显然,当$P$位于$E,F,G$三点当中的一点时,所求距离取得最大值.\\ 设$M$为$CD$中点,连接$AM,BM$,易得$$ |AM|=|BM|=|AB|=8.$$因此$\triangle ABM$为正三角形,过$G$作$AB$的垂线,垂足为$H$,则$|GH|=\sqrt{21}$,当$P$位于$G$点时$$ \begin{split} |BP|&=\sqrt{|BH|^2+|GH|^2}\\ &=\sqrt{\left(|AB|-|GH|\cdot \cot 60^\circ\right)^2+|GH|^2}\\ &=\sqrt{92-16\sqrt{7}}. \end{split} $$ 而当$P$位于$F$点时,过$F$作$AB$的垂线,垂足为$I$,则$|FI|=\sqrt{21}$,易求得$$ \tan \angle CAB=\dfrac{\sqrt{21}}{2}.$$于是$$ \begin{split} |BP|&=\sqrt{|BI|^2+|FI|^2}\\ &=\sqrt{\left(|AB|-|AI|\right)^2+|FI|^2}\\ &=\sqrt{\left(|AB|-\dfrac{|FI|}{\tan\angle CAB}\right)^2+|FI|^2}\\ &=\sqrt{57}. \end{split} $$ 显然,当$P$位于$E$$($或$F)$处时$|BP|$取得较大值$\sqrt{57}$.因此所求距离最大值为$\sqrt{57}$.