已知椭圆\(E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) \((a>b>0)\)的长轴长为\(4\),离心率为\(\dfrac{\sqrt{2}}{2}\).
\((1)\) 求椭圆\(E\)的标准方程;
\((2)\) 过\(P(1,0)\)作直线\(AB\),与椭圆相交于\(A,B\)两点.是否存在定直线\(l\),对于任意给定的直线\(AB\),使得\(l\)上的任意一点\(Q\),与\(A,P,B\)三点连线的斜率始终成等差数列? 若存在,求出该直线方程;若不存在,请说明理由.
解析:
\((1)\) 由题易得椭圆方程为\(\dfrac{x^2}{4}+\dfrac{y^2}{2}=1\).
\((2)\) 假设存在满足题意的直线,则根据对称性,易知该定直线垂直于\(x\)轴,
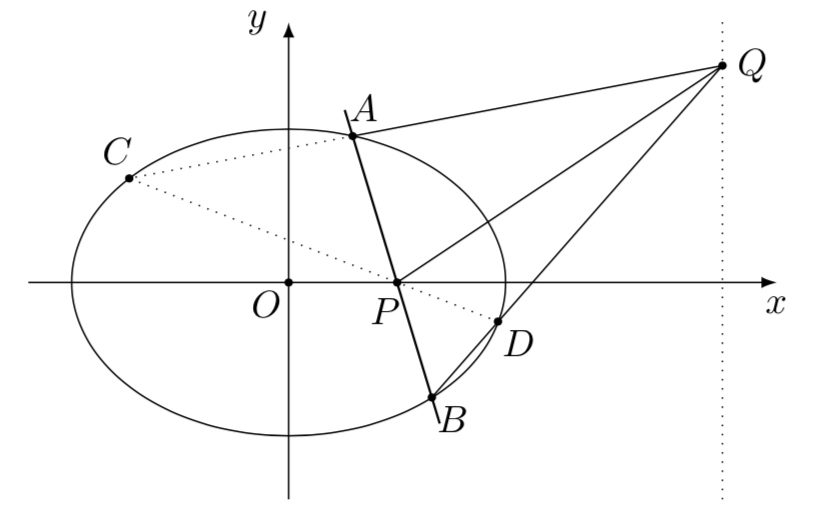
设$QB$直线与椭圆交于另一点$D$,连接$DP$并延长,与椭圆交于另一点$C$,分别记直线$QB,QP,QA,QC$的斜率为$$ k_1,k_0,k_2,k_3.$$ 对于$A,B,Q$构成的点组,满足$$ k_1+k_2=2k_0.$$ 对于$C,D,Q$构成的点组,满足$$ k_3+k_2=2k_0.$$于是对比以上两式可知$k_1=k_3$,因此$C,A,Q$三点共线. 从而结合极点极线的知识可判定$Q$点必然也恒位于$P$点关于椭圆$E$的极线,也即直线$x=4$上 . 存在直线$x=4$满足题意,以下给与证明.设$A(x_1,y_1)$, $B(x_2,y_2)$ ,$Q(4,t)$,$t\in\mathbb{R}$. 情形一 当直线$AB$斜率为$0$,也即$AB$直线与$x$轴重合时,直线$QA,QB$的斜率之和为$$ \dfrac{t-0}{4-(-2)}+\dfrac{t-0}{4-2}=\dfrac{2}{3}t.$$ 此时$QP$的斜率为$\dfrac{t-0}{4-1}=\dfrac{t}{3}$,满足题意. 情形二 当直线$AB$的斜率不为$0$时,设直线$AB$的方程为$$ x=my+1,m\in\mathbb{R}.$$将该直线与椭圆的方程联立消去$x$并整理可得$$(2+m^2)y^2+2my-3=0.$$由韦达定理易得$$ y_1+y_2=\dfrac{-2m}{2+m^2},y_1y_2=\dfrac{-3}{2+m^2}.$$ 从而直线$QA,QB$的斜率之和为$$ \begin{split} \dfrac{t-y_1}{4-x_1}+\dfrac{t-y_2}{4-x_2}&=\dfrac{t-y_1}{3-my_1}+\dfrac{t-y_2}{3-my_2}\\ &=\dfrac{6t-(3+mt)(y_1+y_2)+2my_1y_2}{9-3m(y_1+y_2)+m^2y_1y_2}\\ &=\dfrac{4t\cdot(3+2m^2)}{6\cdot(3+2m^2)}\\ &=2\cdot \dfrac{t}{3}. \end{split} $$ 显然$QA,QB$的斜率和等于$QP$斜率的二倍,满足题设. 因此,存在直线$x=4$满足题意.
