已知函数\(f(x)=\dfrac{6{\ln}x}{x}\),关于\(x\)的不等式\(f^2(x)+af(x)+b^2>0\)有且仅有一个整数解,则实数\(a\)的取值范围是\(\underline{\qquad\qquad}.\)
解析:
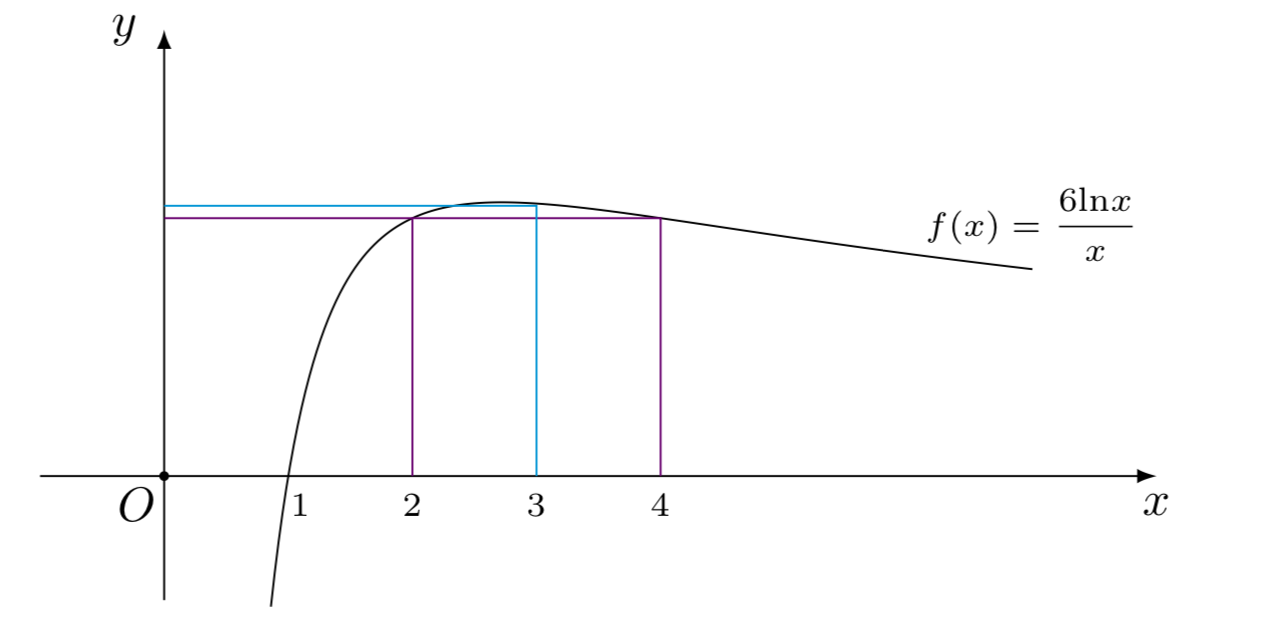
函数\(f(x)\)的图象如图所示
经分析易知$$ \lim_{x\to 0^+}f(x)=-\infty,\quad \lim_{x\to +\infty}f(x)=0^+.$$ 设\(t=f(x)\),则关于\(t\)的方程\(t^2+at+b^2=0\)\((\ast)\)的根有三种情形.
情形一 方程\((\ast)\)无实根,此时由题中所给不等式解出\(t=f(x)\in\mathbb{R}\),显然不满足题意,舍去.
情形二 方程\((\ast)\)有两个相等的实根,记为\(t_0\),此时由题中所给不等式解出$$
t\in\left{t\mid t\in\mathbb{R},t\neq t_0\right}.$$无论\(t_0\)是何值,此时的\(t\),也即\(f(x)\)都不满足题意.
情形三 方程\((\ast)\)有两个不等的实根,记为\(t_1,t_2\),其中\(t_1<t_2\),由韦达定理可知\(t_1t_2=b^2\geqslant 0\).
若\(t_1,t_2\leqslant 0\),此时\(x=2\)和\(x=3\)均满足题中所给不等式,不符题设,舍去.
若\(t_1=0,t_2>0\), 则\(t_2=-a\),此时必须\(t_2\in\left[f(2),f(3)\right)\),即有\(a\in\left(-2{\ln}3,-3{\ln}2\right]\).
若$t_1,t_2>0$,则$$ \forall x\in\left\{x\bigg | x\in\mathbb{N} \text{ 且 } x\geqslant \dfrac{36}{t_1^2} \right\}, f(x)<\dfrac{6\sqrt{x}}{x}=\dfrac{6}{\sqrt{x}}\leqslant t_1.$$ 因此,此时有无数个正整数满足题中所给不等式,不符题设,舍去. 综上可得,所求$a$的取值范围为$\left(-2{\ln}3,-3{\ln}2\right]$.