每日一题_191030

已知$\triangle ABC$的内角$A,B,C$所对的边分别为$a,b,c$,若$a=\sqrt{2}$,$b^2-c^2=6$,则角$A$最大时,$\triangle ABC$的面积等于$\underline{\qquad\qquad}.$
解析:
法一 由题有$$
\begin{split}
\cos A&=\dfrac{b^2+c2-a^{2}{2bc}=\dfrac{b}2+c^2-2}{2bc}\
&=\dfrac{b^2+c2-\dfrac{1}{3}\left(b^2-c2\right)}{2bc}\
&=\dfrac{b}{3c}+\dfrac{2c}{3b}\
&\geqslant \dfrac{2\sqrt{2}}{3}.
\end{split} $$当且仅当$$ \left(\dfrac{b}{3c}=\dfrac{2c}{3b}\right)\land \left(b^2-c2=6\right)$$即$(b,c)=\left(2\sqrt{3},\sqrt{6}\right)$时等号成立.因此$\cos A$的最小值为$\dfrac{2\sqrt{2}}{3}$,此时$A$最大,所求三角形面积为 $$S_{\triangle ABC}=\dfrac{1}{2}bc\sin A=\sqrt2.$$

法二 建立如图所示的平面直角坐标系,设$A(x,y)$,


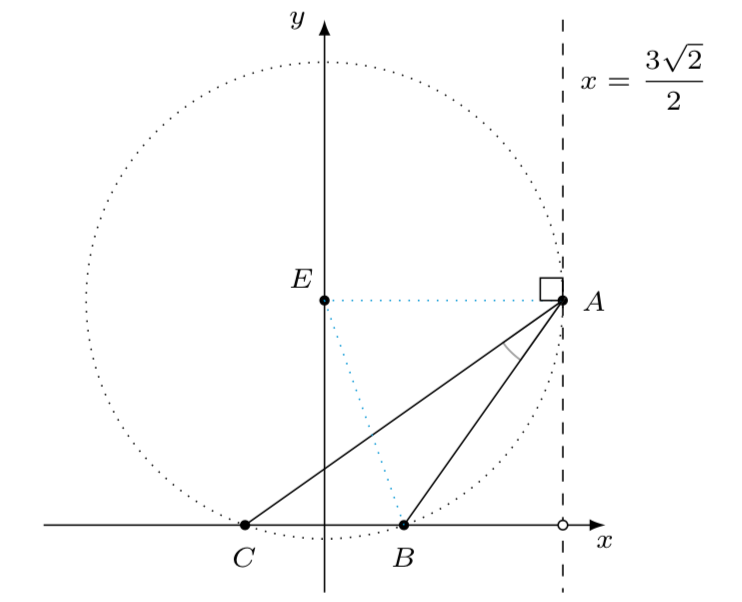
则由$b^2-c^2=6$可得$x=\dfrac{3\sqrt{2}}{2}$.或者由等差幂线知识易知$A$的轨迹为 $$x=\dfrac{3\sqrt{2}}{2},y\neq 0.$$ 于是接下来的问题即求使得$A$角最大的位置,即米勒最大视角问题,当经过$B,C$两点的圆$($记为圆$E)$与$A$的轨迹相切时,$A$角最大. 此时 $$\dfrac{3\sqrt{2}}{2}=|EA|=|EB|=\sqrt{|OE|^2+|OB|^2}.$$ 解得$|OE|=2$.此时$\triangle ABC$的面积为 $$S_{\triangle}=\dfrac{1}{2}\cdot |BC|\cdot |OE|=\sqrt{2}.$$