定义在封闭的平面区域\(D\)内任意两点的距离的最大值称为平面区域\(D\)的``直径''.已知锐角三角形的三个顶点\(A,B,C\)在半径为\(1\)的圆上,且\(\angle BAC=\dfrac{\pi}{3}\),分别以\(\triangle ABC\)各边为直径向外作三个半圆,这三个半圆和\(\triangle ABC\)构成平面区域\(D\),则平面区域\(D\)的"直径"的最大值是\(\underline{\qquad\qquad}\).
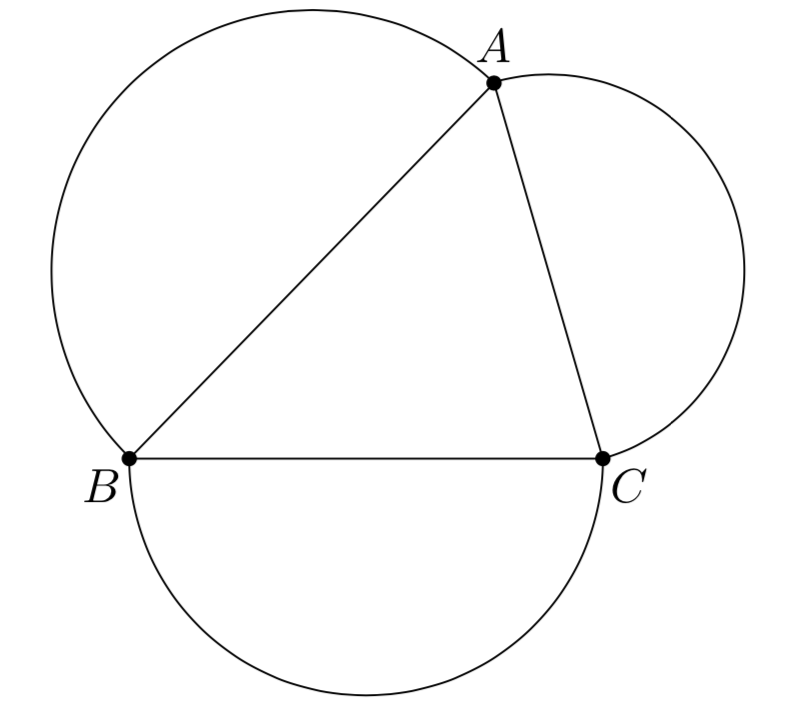
解析: 如图将平面区域\(D\)划分为四块
区域\(\rm I:\)以\(AB\)为直径的半圆\((\)包含周长\()\)区域.
区域\(\rm II:\)以\(BC\)为直径的半圆\((\)包含周长\()\)区域.
区域\(\rm III:\)以\(CA\)为直径的半圆\((\)包含周长\()\)区域.
区域\(\rm IV:\)\(\triangle ABC\)内部的\((\)不包含周长\()\)区域.
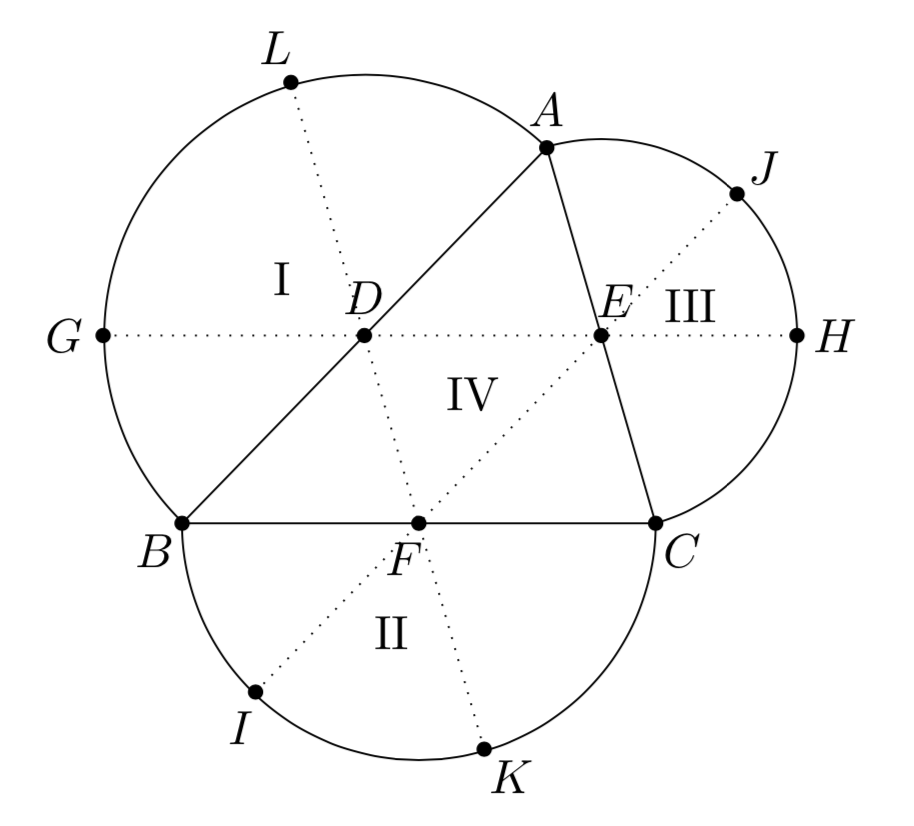
如图,$D,E,F$分别为$\triangle ABC$三边上的中点,分别连接并延长$DE,EF,DF$交区域$D$的边界于$G,H,I,J,K,L$六点, 根据题意,仅需考察以下三组距离的最大值即可$:$ 区域$\rm I$内点到$\rm II$内点的距离,区域$\rm II$内点到$\rm III$内点的距离,区域$\rm I$内点到$\rm III$内点的距离. 而区域$\rm I$内点到区域$\rm II$内点的最大值即$|KL|$,又$$ |DL|=|DB|,|FK|=|FB|.$$ 所以区域$\rm I$内点到区域$\rm II$内点距离的最大值即$\triangle BDF$的周长,记为$C_{\triangle BDF}$,于是原题转化为求$$ \mathrm{max}\left\{C_{\triangle BDF},C_{\triangle CEF},C_{\triangle ADE} \right\}.$$ 而$$C_{\triangle BDF}=C_{\triangle CEF}=C_{\triangle ADE}=\dfrac12C_{\triangle ABC}.$$于是问题进一步转化为求$\triangle ABC$周长的最大值,也即求$AB+AC$的最大值,分别记$$ (BC,AC,AB)=(a,b,c).$$则由余弦定理$$ b^2+c^2-a^2=2bc\cos A=bc.$$于是$$ (b+c)^2-3=3bc\leqslant \dfrac{3}{4}\left(b+c\right)^2.$$所以$b+c$的最大值为$2\sqrt3$,当且仅当$b=c=\sqrt3$时取得,因此平面区域$D$的``直径''的最大值为$\dfrac{3\sqrt{3}}{2}$.