每日一题_190912

已知椭圆 \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) \((a>b>0)\) 的左右焦点分别为 \(F_1(-c,0)\), \(F_2(c,0)\), 动弦 \(AB\) 过左焦点, 若 $\left| \overrightarrow{F_2A}- \overrightarrow{F_2B} \right| \geqslant \left| \overrightarrow{F_2A}+ \overrightarrow{F_2B} \right| $ 恒成立, 则椭圆的离心率的取值范围是\(\underline{\qquad\qquad}\).
解析: 如图, 设直线 \(AB\) 的倾斜角为 \(\theta\), 则 \(\theta\) 的取值范围为 \([0,\pi)\),

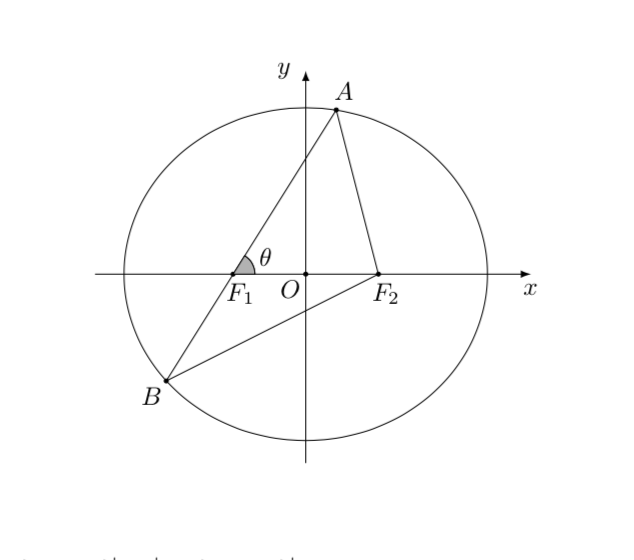
对题中所给条件不等式 \(\left| \overrightarrow{F_2A}- \overrightarrow{F_2B} \right| \geqslant \left| \overrightarrow{F_2A}+ \overrightarrow{F_2B} \right|\) 两边平方可化简为
$$
\overrightarrow{F_2A}\cdot \overrightarrow{F_2B}\leqslant 0.
$$ 即

\[\forall \theta\in[0,\pi), \left( \overrightarrow{F_2F_1}+\overrightarrow{F_1A} \right)\cdot \left(\overrightarrow{F_2F_1}+\overrightarrow{F_1B} \right)\leqslant 0,$$ 记上述不等式左侧为 $LHS$, 则 \]

	\begin{split}
		 LHS =&\overrightarrow{F_2F_1}^2+\overrightarrow{F_2F_1}\cdot \overrightarrow{F_1A}+\overrightarrow{F_2F_1}\cdot \overrightarrow{F_1B}+\overrightarrow{F_1A}\cdot\overrightarrow{F_2B}\\
		 =&4c^2-2c\cdot \dfrac{b^2}{a-c\cos\theta}\cdot \cos\theta+2c\cdot \dfrac{b^2}{a+c\cos\theta}\cdot \cos\theta \\

&-\dfrac{b^2}{a-c\cos\theta}\cdot \dfrac{b^2}{a+c\cos\theta} \
=& \dfrac{4a^2c2\sin^2\theta -b^4}{a2-c^2\cos2\theta}.
\end{split}$$ 从而 $$
\forall \theta\in[0,\pi), 4a^2c2 \sin^2\theta-b4\leqslant 0. $$
于是可得 \(4a^2c^2-b^4\leqslant 0\). 若记椭圆离心率为 \(e=\dfrac ca\), 则有
$$
e^2+2e-1\leqslant 0, e\in (0,1).
$$ 解得 \(e\) 的取值范围为 \(\left(0,\sqrt2-1\right )\).