JTX发的一道题

题目

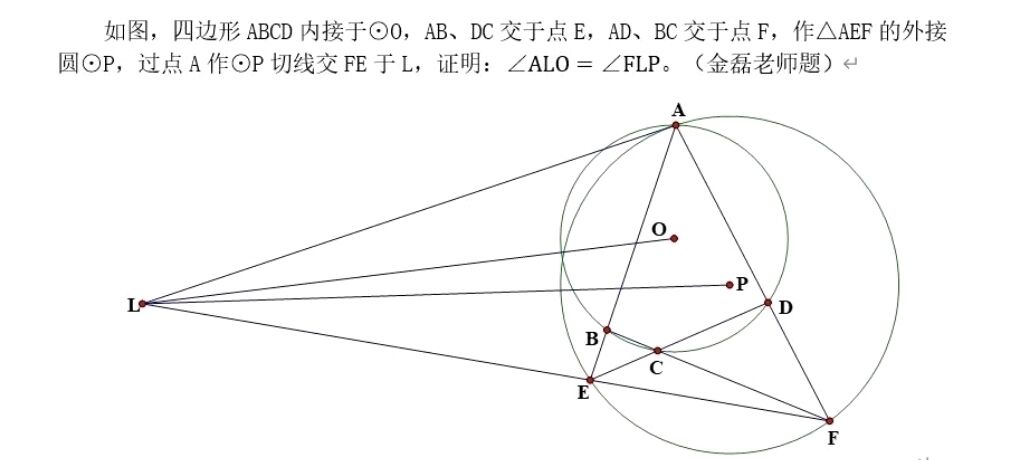
Geogebra作图

证明：

作出完全四边形ABECFD的密克尔点G，连接OG，作EF中点M，过点O作LA垂线并交于点N；
设$\angle OLN=\alpha,\angle FLP=\beta,\angle ALF=\gamma$

$先证明G在EF上且OG\bot EF$

$$\angle EGC+\angle EGF=\angle ABC+\angle ADC=180^\circ$$

$$OE^2-OF^2=EB\cdot EA-FD\cdot FA=EG\cdot EF-FG\cdot FE=EG^2-FG^2$$

设圆$O$半径为$r$

$$OG^2=OE^2-EG^2=EG\cdot EF+r^2-EG^2=EG\cdot FG+r^2$$

计算点$L$对圆$O$的幂

$$\begin{align} &LA\cdot(2LN-LA)=OL^2-r^2=OG^2+GL^2-r^2\\ \Leftrightarrow &2LA\cdot LN-LA^2=OG^2+LG^2-r^2 \\\Leftrightarrow &2LA\cdot LN=LA^2+EG\cdot FG+r^2+LG^2-r^2=LM\cdot LG \end{align}$$

即点ANGM四点共圆

$$\begin{align} 0&=LN\cdot LA-LG\cdot LM\\ &=OL \cos\alpha\cdot PL \cos(\gamma-\beta)-OL\cos(\gamma-\alpha)\cdot PL\cos\beta\\ &=OL\cdot PL (\cos\alpha\cos(\gamma-\beta)-cos\beta\cos(\gamma-\alpha))\\ &=OL\cdot PL \sin\gamma \sin(\beta-\alpha) \end{align}$$

即证$\alpha=\beta$