《高等应用数学问题的MATLAB求解》——第2章习题代码
(1)书上的代码
tic,A=rand(500);B=inv(A);norm(A*B-eye(500)),toc
(2)转化为latex的代码有问题,换元没问题
syms x s;y=x^5+3*x^4+4*x^3+2*x^2+3*x+6;y1=simplify(subs(y,x,(s-1)/(s+1)))
(3)
>> syms k int;
>> simplify(sin(k*pi+pi/6))
(4)使用sym和vpa,这里可以看出sym是针对于常数的
\(\sqrt 2\): vpa(sqrt(sym(2)),200)
\(\sqrt[6]{11}\):vpa((sym(11))^(1/6),200)
\(\sin 1^\circ\):vpa(sin(pi/sym(90)),200)
\(e^2\):vpa(exp(sym(2)),200)
\(\ln (21)\):vpa(log(sym(21)),200)
\(\log_2(e)\):vpa(log2(exp(sym(1))),200)
(5)①是正确的
vpa(log10(sym(12345678)))
(6)代入化简
\(e^{j\pi}+1=0\):exp(sym(j)*pi)+sym(1)
\(\frac{1-2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}=\frac{1-\tan\alpha}{1+\tan\alpha}\)simplify((1-2*sin(alpha)*cos(alpha))/(cos(alpha)^2-sin(alpha)^2)-(1-tan(alpha))/(1+tan(alpha)))
(7)\(f(x)=x^2-x-1,f(f(f(f(f(f(f(f(f(f(f(x))))))))))\)
syms x;f=@(x)x^2-x-1;size(coeffs(f(f(f(f(f(f(f(f(f(f(x)))))))))),x),2)-1
(8)
>> v=3:11;A=rand(v);B=reshape(A,numel(A),1);mean(B)
(9)
>> syms x;f(x)=x*sin(x)/(sqrt(x^2+2)*(x+5));g(x)=tan(x);
>> simplify(f(g(x))),simplify(g(f(x)))
(10)\(\binom{50}{10}\)
双精度:vpa(factorial(50)/(factorial(10)*factorial(40)))
符号型:factorial(sym(50))/(factorial(sym(10))*factorial(sym(40)))
nchoosek:nchoosek(sym(50),10)
(11)\((12!,12039287653026128192934)\)
gcd(factorial(sym(12)),sym(12039287653026128192934))
(12)\(P(x)=x^5+10x^4+34x^3+52x^2+37x+10,Q(x)=x^5+15x^4+79x^3+177x^2+172x+60\),\((P,Q)=x^4+9x^3+25x^2+27x+10\)
syms x;P=x^5+10*x^4+34*x^3+52*x^2+37*x+10;Q=x^5+15*x^4+79*x^3+177*x^2+172*x+60;gcd(P,Q)
(13)\((0,1000]\)以及\([3000,5000]\)可以被11整除的数
vec=[];
for k=1:1000
if(mod(k,11)==0)
vec=[vec,k];
end
end
vec2=[];
for k=3000:5000
if(mod(k,11)==0)
vec2=[vec2,k];
end
end
(14)
>> v=[];for k=1:1000,if isprime(k)==1,v=[v,k];end;end
(15)
>>A=magic(100);A(find(A>1000))=0;
(16)
>> [row column]=find(A==34438)
(17)
>> tic,s=0;m=sym(1);for k=1:1e+5,if isprime(k)==1,s=s+1;m=m*k;end;end,toc
(18)
>> A=[1,2,3,4;4,3,2,1;2,3,4,1;3,2,4,1];B=[1+4j,2+3j,3+2j,4+1j;4+1j,3+2j,2+3j,1+4j;2+3j,3+2j,4+1j,1+4j;3+2j,2+3j,4+1j,1+4j];
>> A(5,6)=5
(19)
>> A=magic(8);B=A(2:2:end,:)
(27)
>> x1=1;x2=x1/2+3/(2*x1);n=2;
>> while abs(x1-x2)>1e-14,x1=x2;x2=x2/2+3/(2*x2);n=n+1;end
(28)
>> S=1;n=1;S1=S*(1+2/n^2);
>> while abs(S1-S)>1e-12,n=n+1;S=S1;S1=S*(1+2/n^2);end
(29)
>> v=[];for m=1:9,for n=0:9,for k=0:9,if m^3+n^3+k^3==100*m+10*n+k;v=[v,100*m+10*n+k];end,end,end,end
(30)
n=3;T1=1;T2=1;T3=1;v=[T1,T2,T3];while n<300,v=[v,T1+T2+T3];T3=v(end);T2=v(end-1);T1=v(end-2);n=n+1;end
(32)
>> n=2;PI=2;delta=n^2/(n^2-1);
>> while (delta-1)>1e-6,PI=PI*delta;n=n+2;delta=n^2/(n^2-1);end
>> delta=sqrt(2);PI=1;while abs(delta/2-1)>1e-6,PI=PI*delta/2;delta=sqrt(delta+2);end
>> PI=2/PI;
(33)
1
>> syms x;f(x)=x^2*sin(0.1*x+2)-3;a=-4;b=0;
>> while abs(f((a+b)/2))>1e-10
if f((a+b)/2)*f(a)<0
b=(a+b)/2;
else
a=(a+b)/2;
end
end
>> vpa(f((a+b)/2))
2
>> syms x;f(x)=x^2*sin(0.1*x+2)-3;fx(x)=diff(f(x));x0=-4;x1=x0-f(x0)/fx(x0);
>> while abs(x1-x0)>1e-12,x0=x1;x1=x1-f(x1)/fx(x1);end
(37)矩阵反演\(M^{-1}=(A+BCB^T)^{-1}=A^{-1}-A^{-1}B(C^{-1}+B^TA^{-1}B)^{-1}B^TA^{-1}\)
编写函数:
function Temp=my_inv(A,B,C)
A_inv=inv(A);
C_inv=inv(C);
Temp=A_inv-A_inv*B*inv(C_inv+B'*A_inv*B)*B'*A_inv;
测试函数:
M=[-1 -1 -1 1 0;-2 0 0 -1 0; -6 -4 -1 -1 -2; -1 -1 0 2 0; -4 -3 -3 -1 3];
A=diag([1,3,4,2,4]);
B=[0 1 1 1 1; 0 2 1 0 1;1 1 1 2 1; 0 1 0 0 1;1 1 1 1 1];
C=[1 -1 1 -1 -1;1 -1 0 0 -1;0 0 0 0 1;1 0 -1 -1 0;0 1 -1 0 1];
my_inv(A,B,C)-inv(M);
(38)
(39)①\(f(x)=x\sin x,x\in(-50,50);②f(x)=x\sin\frac{1}{x},x\in(-1,1)\)
x1=linspace(-50,50);x2=linspace(-1,1);
y1=x1.*sin(x1);y2=x2.*sin(1./x2);
plot(x1,y1);figure;plot(x2,y2)
(40)
(42)\(-50\leq x,y \leq 50 ,x\sin x+y\sin y=0\)
ezplot('x*sin(x)+y*sin(y)',[-50,50])
(43)\(\sin\frac{1}{t},t\in(-1,1)\)
t=[-1:0.01:0.1,-0.1:0.0001:0.1,0.1:0.01:1];
plot(t,sin(1./t))
(44)极坐标图形:\(\rho=1.0013\theta^2\);\(\rho=\frac{1}{2}\cos7\theta\);\(\rho=\frac{\sin\theta}{\theta}\);\(\rho=1-\cos^37\theta\).
theta=0:0.01:2*pi;
rho1=1.0013.*theta.^2;
rho2=cos(7*theta)/2;
rho3=sin(theta)./theta;
rho4=1-cos(7*theta).^3;
polar(theta,rho1);
figure;polar(theta,rho2);
figure;polar(theta,rho3);
figure;polar(theta,rho4);
(45)
>> ezplot('x^2+y^2-3*x*y^2');hold on,ezplot('x^3-x^2-y^2+y')
>> clear;clc
>> ezplot('exp(-(x+y)^2+pi/2)*sin(5*x+2*y)'),hold on,ezplot('(x^2-y^2-x*y)*exp(-x^2-y^2-x*y)')
(46)\(W(z)e^{W(z)}=z\)
ezplot('y*exp(y)-x')
(47)
>> t=0:.1:2*pi; a=1/2; b=1/3; x=sin(t); y=sin(a*t); z=sin(b*t);
>> plot3(x,y,z)
>> t=0:.1:2*pi; a=2^(1/8); b=3^(1/2); x=sin(t); y=sin(a*t); z=sin(b*t);
>> plot3(x,y,z)
(48)
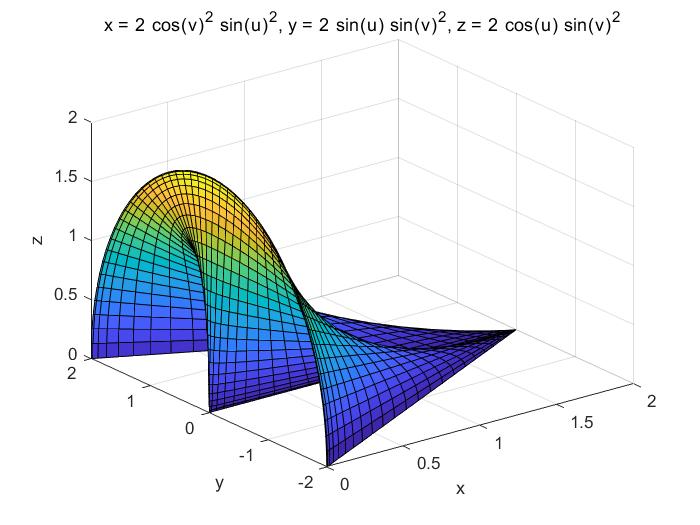
>> syms u v; x=2*sin(u)^2*cos(v)^2; y=2*sin(u)*sin(v)^2;z=2*cos(u)*sin(v)^2;
>> ezsurf(x,y,z,[-pi/2,pi/2,-pi/2,pi/2])
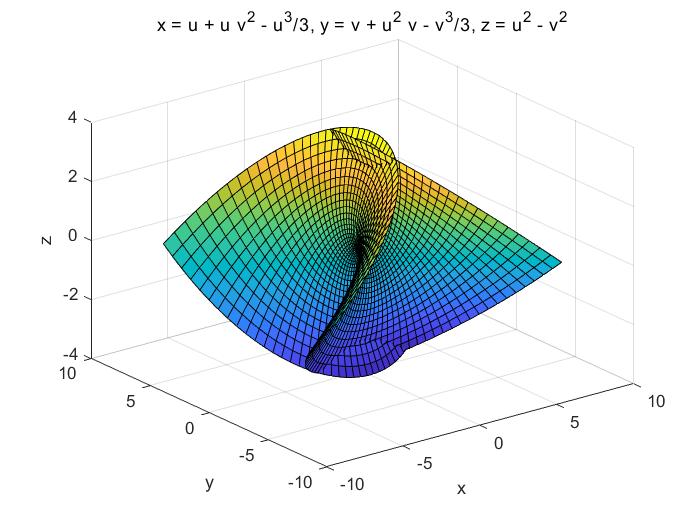
>> syms u v;x=u-u3/3+u*v2;y=v-v3/3+v*u2;z=u2-v2;
>> ezsurf(x,y,z,[-2,2,-2,2])
(49)\(xy,\sin(xy),e^{\frac{2x}{x^2+y^2}}\),第三个趋于0有问题
x=linspace(-1,1);y=linspace(-1,1);[xx,yy]=meshgrid(x,y);
zz1=xx.*yy;zz2=sin(xx.*yy);zz3=exp(2*xx./(xx.^2+yy.^2));
mesh(xx,yy,zz1);figure;surf(xx,yy,zz1);figure;contour(xx,yy,zz1);
figure;mesh(xx,yy,zz2);figure;surf(xx,yy,zz2);figure;contour(xx,yy,zz2);
figure;mesh(xx,yy,zz3);figure;surf(xx,yy,zz3);figure;contour(xx,yy,zz3);
(50)
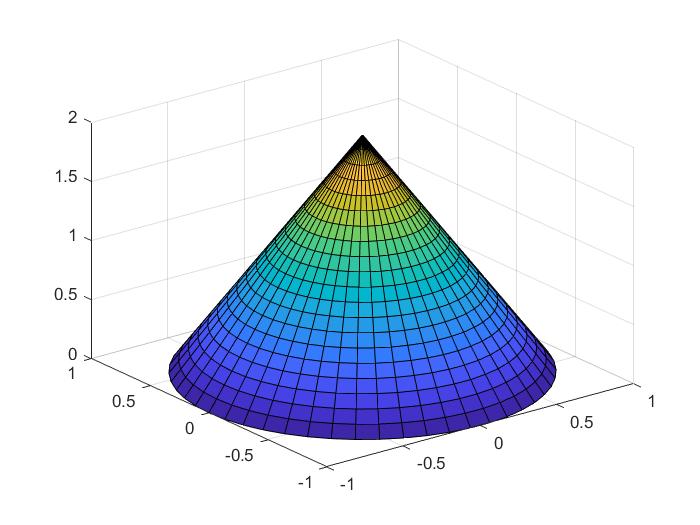
>> z0=0:.1:2;r=(2-z0)/2;[x y z]=cylinder(r,50);z=2*z;surf(x,y,z)
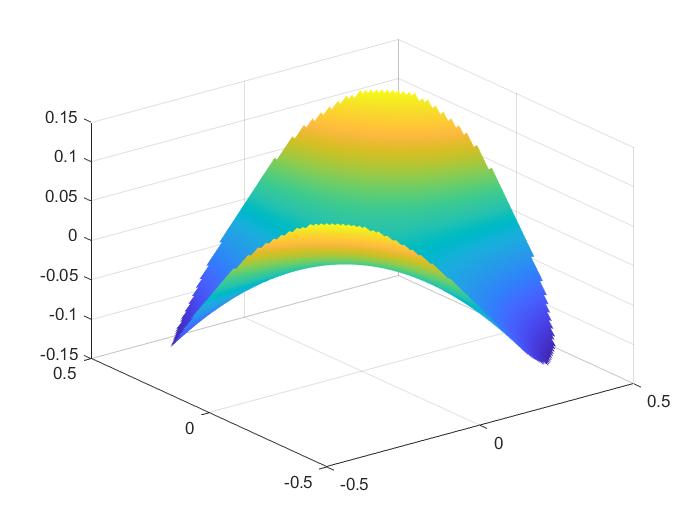
(51)
>> [x y]=meshgrid(-1:.01:1,-1:.01:1);z=x.*y./(x.^2+y.^2<=0.25);surf(x,y,z);shading interp
(52)\(f(x,y)=\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}},-8\leqslant x,y\leqslant 8\)
[X Y]=meshgrid(linspace(-8,8),linspace(-8,8));
surf(X,Y,sin(sqrt(X.^2+Y.^2))./sqrt(X.^2+Y.^2));
shading interp;
(53)不同方向不同半径(修改\(r\))的球面,\(\begin{cases}x=r\sin u\\y=r\cos u\\z=v\end{cases}\)
>> syms u v;r=sym(1);
>> x=r*sin(u);y=r*cos(u);z=v;
>> ezsurf(x,y,z,[0,2*pi,-1,1])
>> ezsurf(x,z,y,[0,2*pi,-1,1])
>> ezsurf(z,x,y,[0,2*pi,-1,1])
(54)分别使用surfc、surfl、waterfall绘制\(z=xy\)、\(z=\sin(x^2y^3)\)、\(z=\frac{(x-1)^2y^2}{(x-1)^2+y^2}\)、\(z=-xye^{-2(x^2+y^2)}\)
>> [X,Y]=meshgrid(linspace(-2,2),linspace(-2,2));
>> Z1=X.*Y;
>> Z2=sin(X.^2.*Y.^3);
>> Z3=(X-1).^2.*Y.^2./((X-1).^2+Y.^2);
>> Z4=-X.*Y.*exp(-2*(X.^2+Y.^2));
>> subplot(3,4,1),surfc(X,Y,Z1);shading interp;
>> subplot(3,4,2),surfc(X,Y,Z2);shading interp;
>> subplot(3,4,3),surfc(X,Y,Z3);shading interp;
>> subplot(3,4,4),surfc(X,Y,Z4);shading interp;
>> subplot(3,4,5),surfl(X,Y,Z1);shading interp;
>> subplot(3,4,6),surfl(X,Y,Z2);shading interp;
>> subplot(3,4,7),surfl(X,Y,Z3);shading interp;
>> subplot(3,4,8),surfl(X,Y,Z4);shading interp;
>> subplot(3,4,9),waterfall(X,Y,Z1);
>> subplot(3,4,10),waterfall(X,Y,Z2);
>> subplot(3,4,11),waterfall(X,Y,Z3);
>> subplot(3,4,12),waterfall(X,Y,Z4);
(55)\((x^2+xy+xz)e^{-z}+z^2yx+\sin(x+y+z^2)\)
>> f='(x^2+x*y+x*z)*exp(-z)+z*z*y*x+sin(x+y+z^2)';
>> ezimplot3(f)
(56)
>> ezimplot3('x^2+y^2+z^2-64',[-10,10]);
>> hold on,ezimplot3('y+z')


 浙公网安备 33010602011771号
浙公网安备 33010602011771号