C++ 按照字典序实现combination
C++ 按照字典序实现combination
引言
C++ STL提供了permutation相关的函数（std::next_permutation和std::prev_permutation），但是没有提供combination相关的函数，本文将基于字典序的方法实现一个combination相关的函数。
算法回顾
1.permutation用法
C++的permutation是基于字典序实现的，从一个初始有序的序列出发对元素进行重新排列，当排列到最后一个字典序的时候该函数返回false，否在返回true，具体如下：
std::vector vec = { 1, 2, 3 };
std::sort(vec);
do {
// ...
} while (std::next_permutation(vec.begin(), vec.end()));
2.字典序
假设S是由连续的整数构成的序列：
设A和B是集合S的两个r子集，其中r是满足 \(1 \leq r \leq n\)的固定整数。如果在并集\(A \cup B\)但不在交集\(A \cap B\)中的最小整数在A中，我们就认为在字典序中A先于B。
举个例子：假设\(A = \{2, 3, 4, 7, 8\}, B = \{2, 3, 5, 6, 7\}\)，不难发现\(A \cap B = \{2, 3, 7\} , A \cup B = \{2, 3, 4, 5, 6, 7, 8\}\)，其中4是在\(A \cup B\)中但是不在\(A \cap B\)中的最小整数，它在A中，所以A的字典序是小于B的。
3.元素重复问题
组合数是不关注元素顺序的，对于\(\{1, 2\}\)和\(\{2, 1\}\)是俩个相同的集合。所以我们约定当我们书写集合\(S = \{a_1, a_2, ..., a_n\}\)时，必有\(1 \le a_1 \lt a_2 \lt a_3 \lt ... \lt a_r \le n\)。这样对于对于\(\{1, 2\}\)和\(\{2, 1\}\)来说，它们最终的写法都是\(\{1, 2\}\)。按照这种方式，我们回顾一下刚才的俩个集合
我们将A和B对齐之后不难发现在第三个元素的位置4是小于5的，所以A的字典序是小于B的。
算法实现
1.算法原理
假设初始序列是\(\{1, 2, 3, 4\}\)，我们需要求解3子集的字典序，第一个3子集是\(\{1, 2, 3\}\)最后一个3子集是\(\{2, 3, 4\}\)。那么\(\{1, 3, 4\}\)的后继是多少呢？
不难发现此时的以1开始的序列中3, 4已经是最大值了，那么接下来应该是以2开头的序列，即\(\{2, 3, 4\}\)
定理：设\(a_1a_2...a_r\)是\(\{1, 2, ..., n\}\)的\(r\)子集。在字典序中，第一个\(r\)子集是\(12...r\)。最后一个\(r\)子集是\((n-r+1)(n-r+2)...n\)。假设\(a_1a_2...a_r \ne (n-r+1)(n-r+2)...n\)。设\(k\)是满足\(a_k \lt n\)且使得\(a_k+1 \notin \{a_1, a_2, ..., a_r\}\)的最大整数，那么在字典序中，\(a_1a_2...a_r\)的直接后继\(r\)子集是\(a_1...a_{k-1}(a_k+1)(a_k+2)...(a_k+r-k+1)\)。
2.算法证明
根据字典序的定义，\(12...r\)是在字典序的第一个\(r\)子集，而\((n-r+1)(n-r+2)...n\)是最后一个\(r\)子集。现在，设\(a_1a_2...a_r\)是任意一个\(r\)子集，但不是最后一个\(r\)子集，确定出定理中的\(k\)。于是
其中
因此，\(a_1a_2...a_r\)是以\(a_1a_2...a_{k-1}a_k\)开始的最后的\(r\)子集。而下面的\(r\)子集
是以\(a_1...a_{k-1}a_k+1\)开始的第一个\(r\)子集，从而是\(a_1a_2...a_r\)的直接后继。
3.具体实现
我们首先按照STL风格来定义我们的函数接口：
template <typename I, typename Comp>
constexpr bool combination(I first, I middle, I last, Comp comp);
和permutation不同的是，combination需要一个参数告诉我们子集\(r\)的大小，比如对于一个有6个元素的序列的4子集来说，我们可以通过以下方式去调用我们的函数：
combination(sequence.begin(), sequence.begin() + 4, sequence.begin() + 6, std::less<>());
接下来我们来梳理一下算法。
假设\(S = \{1, 2, ..., n \}\)，从\(r\)子集\(a_1a_2...a_r\)开始。
当\(a_1a_2...a_r \ne (n-r+1)(n-r+2)...n\)时执行下列操作：
(1) 确定最大的整数\(k\)使得\(a_k+1 \le n\)且\(a_k+1 \notin \{a_1, a_2, ..., a_r\}\)。
(2) 用\(r\)子集\(a_1...a_{k-1}(a_k+1)(a_k+2)...(a_k+r-k+1)\)替换\(a_1a_2...a_r\)。
我们使用\(left\)来指向\(a_k\)，由于左半部分是递增序列，我们可以通过反向遍历左半部分来获其所在的位置：
auto left = middle, right = last;
--right; --left;
for (; left != first && !comp(*left, *right); --left);
这里有两个问题需要注意:
1、如何找到\(a_k+1\)。
\(a_k+1\)实际上可以看成是原序列中\(a_k\)的后面那一个元素，比如当\(S=\{1,2,3,4\}, a_k=2\)时，\(a_k\)后面的元素是3。当\(S=\{1,2,4,5\}, a_k=2\)时，\(a_k\)后面的元素是4。
由于右半部分也是递增序列，我们可以通过正向遍历右半部分来获取其位置
for (right = middle; right != last && !comp(*left, *right); ++right);
2、如何准确的找到\(\{1,3,4,5\}\)来替换\(\{1,2,5,6\}\)。
我们可以使用强大的观察法来尝试发现规律。
我们使用\(left\)来指向\(a_k\)， 使用\(right\)来指向\(a_k+1\)，同时我们将这两个元素标红。同时，我们将处于\([left+1, middle)\)和\([right+1,last)\)内的元素标蓝。
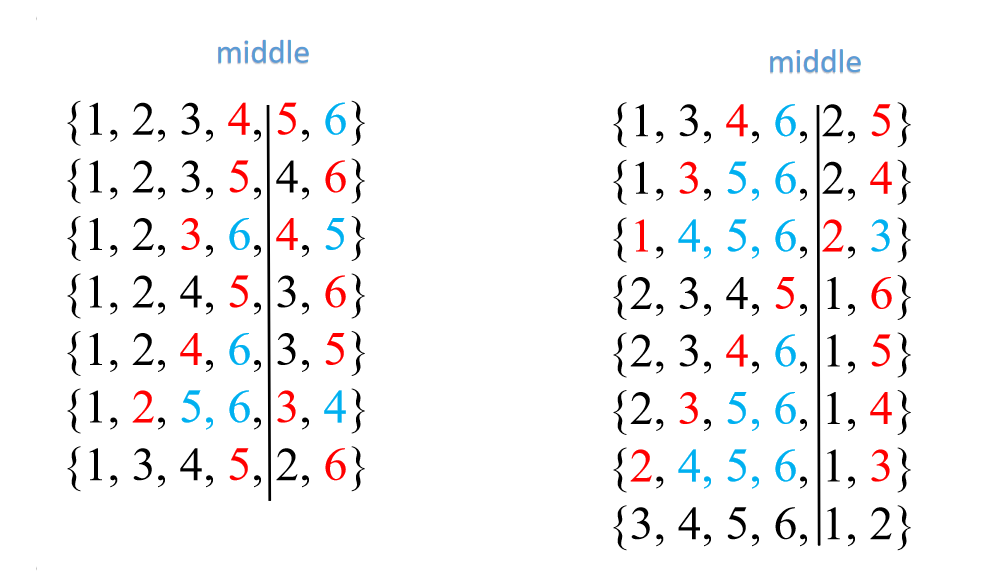
不难发现，我们只需要将红色的元素交换，并将蓝色的元素左移就可以获得该序列的后继序列。
比如\(\{1, 2, 5, 6, 3, 4\}\)，我们首先交换红色部分得到\(\{1, 3, 5, 6, 2, 4\}\)，然后将蓝色部分的\(\{5,6,4\}\)左移2个单位得到\(\{4,5,6\}\)最后再放回该序列就可以得到\(\{1,3,4,5,2,6\}\)
代码如下：
bool is_over = left == first && !comp(*first, *right);
right = middle;
if (!is_over)
{
for (; right != last && !comp(*left, *right); ++right);
std::iter_swap(left++, right++);
}
shift_left(left, middle, right, last);
关于shift_left的代码我们只需要将std::rotate中的相关变量名称修改一下即可，这里不再考虑具体实现和优化。
template <typename I>
void shift_left(I first1, I last1, I first2, I last2)
{
if (first1 == last1 || first2 == last2)
return;
std::reverse(first1, last1);
std::reverse(first2, last2);
while (first1 != last1 && first2 != last2)
{
std::iter_swap(first1, --last2);
++first1;
}
if (first1 == last1)
{
std::reverse(first2, last2);
}
else
{
std::reverse(first1, last1);
}
}
全部代码如下：
template <typename I>
void shift_left(I first1, I last1, I first2, I last2)
{
if (first1 == last1 || first2 == last2)
return;
std::reverse(first1, last1);
std::reverse(first2, last2);
while (first1 != last1 && first2 != last2)
{
std::iter_swap(first1, --last2);
++first1;
}
if (first1 == last1)
{
std::reverse(first2, last2);
}
else
{
std::reverse(first1, last1);
}
}
template <typename I, typename Comp>
constexpr bool combination(I first, I middle, I last, Comp comp)
{
if (first == middle || middle == last)
return false;
auto left = middle, right = last;
--right;
--left;
// The left should less than right.
for (; left != first && !comp(*left, *right); --left);
// If all elements in left is greater than right, the iteration should be stopped.
bool is_over = left == first && !comp(*first, *right);
right = middle;
if (!is_over)
{
// Find a_k + 1
for (; right != last && !comp(*left, *right); ++right);
std::iter_swap(left++, right++);
}
// Replace (a_1, ..., a_{k-1}) with (a_k + 1, ..., a_k + r - k + 1)
shift_left(left, middle, right, last);
// Return false to stop do-while loop.
return !is_over;
}
我们可以使用leetcode90来验证算法的正确性：
class Solution {
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
vector<vector<int>> res;
auto comp = less<>();
res.emplace_back(nums);
for (int i = 0; i < nums.size(); ++i) {
sort(nums.begin(), nums.end(), comp);
do {
res.emplace_back(nums.begin(), nums.begin() + i);
} while (combination(nums.begin(), nums.begin() + i, nums.end(), comp));
}
return res;
}
};
参考文献
Introductory Combinatorics (5th Edition) by Richard A. Brualdi (Author)
