抽象代数预习笔记

lash elephant kangaroo（抽🐘袋鼠）

抽象代数里有些语言还是比较严谨的，尽可能保持原样。

这英语不会翻译啊，乱翻译了，保留一下英语名称。

一、群

1.1 定义

群：一个有序二元组 $(G, *)$，其中 $G$ 是集合，$*$ 是二元运算，满足：

1. 结合律：$\forall a, b, c\in G, (a*b)*c=a*(b*c)$
2. 单位元：$\exist e\in G, \forall a\in G, a*e=e*a=a$，$e$ 称为单位元
3. 逆元性：$\forall a\in G, \exist a^{-1}\in G, a*a^{-1}=a^{-1}*a=e$，$a^{-1}$ 称为 $a$ 的逆元

阿贝尔群：群的基础上同时满足交换律 $\forall a, b\in G, a*b=b*a$

群的命题：

1. 单位元 $e$ 唯一，思路：假设 $f, g$ 都是，由群的性质 2 得到 $f=g$
2. $a$ 的逆元唯一，思路：假设 $b, c$ 都是，那么 $c=c*e=c*(a*b)=(c*a)*b=e*b=b$
3. $(a^{-1})^{-1}=a$，思路：通过上一条和群的性质 3 得到
4. $(a*b)^{-1}=(b^{-1})*(a^{-1})$，思路：设 $c=(a*b)^{-1}$，反复使用已有性质
5. 广义结合律，即 $n$ 个数的结合律，思路：归纳法，让任何括号顺序等于到一个很简单的括号顺序

群的命题，令 $a, b\in G$，方程 $ax=b$ 和 $ya=b$ 有唯一解 $x, y\in G$，也就是消去律：

1. 如果 $au=av$，那么 $u=v$
2. 如果 $ub=vb$，那么 $u=v$

群元素的阶（order）：最小正整数 $n$ 使得 $x^n=1$，把它记为 $|x|$，如果不存在则为无穷大

1.2 二面体群（dihedral groups）

也就是一个正 $n$ 边形，允许旋转 $r$ 与翻转 $s$，所有本质不同操作组成的群 $|D_{2n}|=2n$。使用排列来表示，则节点 $i$ 操作后跑到 $\sigma(i)$，二元运算 $st$ 为先做 $t$ 再做 $s$（函数复合）。旋转、翻转的性质有：$|r|=n$, $|s|=2$, $s\neq r^i$, $sr^i\neq sr^j (0\leq i, j \leq n-1, i\neq j)$, $r^is=sr^{-i}$

生成（generators）和关系（relations）：群 $G$ 的一个子集 $S$，如果任意群元素能被写成 $S$ 内元素与其逆元的积，那么 $S$ 就是 $G$ 的生成，$G=\langle S\rangle$（有限群甚至不需要用 $S$ 的逆元）。关系是 $S$ 的关于其元素的积的等式，例如上一段的例子。

表示（presentation）：如果群 $G$ 有生成 $S$ 和一些关系 $R_1, \cdots, R_m$（每个是一个等式），且所有的关系都能被它们推出，那么把这些生成和关系成为 $G$ 的表示，$G=\langle S \mid R_1, \cdots, R_m \rangle$。例如，$D_{2n}=\langle r, s \mid r^n=s^2=1, rs=sr^{-1}\rangle$。

（但是这玩意有的时候很难直观表示群，因为有一些极其隐藏的等式）

1.3 对称群（symmetric groups）

也就是所有排列组成的群，二元运算即为复合（注意运算顺序）。大小为 $n$ 的排列，对称群为 $S_n$。排列可以写成环的集合，长度为 $1$ 的环省略不写，单位元直接写为 $1$。

1.4 矩阵群（matrix groups）

数域（field）$F$ 是指 $(F, +)$ 一个阿贝尔群，$(F-\{0\}, *)$ 也是个阿贝尔群，且满足分配律。记 $F^\times=F-\{0\}$。

$GL_n(F)$ 是以 $F$ 为数域的 $n\times n$ 的行列式非零矩阵与乘法运算构成的群。

书上给了两个结论，但证明在之后的部分：

1. 如果 $F$ 是数域且 $|F|<\infty$，那么 $|F|=p^m$ 其中 $p$ 是质数，$m$ 是整数
2. 如果 $|F|=q<\infty$，那么 $|GL_n(F)|=(q^n-1)(q^n-q)(q^n-q^2)\cdots (q^n-q^{n-1})$

1.5 四元数群（quaternion group）

$Q_8=\{1, -1, i, -i, j, -j, k, -k\}$，乘法定义为

• $1\cdot a=a\cdot 1=a, \forall a\in Q_8$
• $(-1)\cdot (-1)=1, (-1)\cdot a=a\cdot (-1)=-a, \forall a\in Q_8$
• $i\cdot i=j\cdot j=k\cdot k=-1$
• $i\cdot j=k, j\cdot i=-k$
• $j\cdot k=i, k\cdot j=-i$
• $k\cdot i=j, i\cdot k=-j$

1.6 同态（homomorphism）与同构（isomorphism）

设 $(G, \star)$, $(H, \diamond)$ 是群，映射 $\varphi: G\to H$ 满足 $\varphi(x\star y)=\varphi(x)\diamond\varphi(y), \forall x, y\in G$，称之为一个同态。

一个同态 $\varphi$ 如果还满足了双射，那么称为一个同构，记作 $G\cong H$。

一种用 presentation 来检验 $G, H$ 是否是同态（同构）的方法：如果把 G 的 generator 替换成 H 的元素，并保持了 G 的 relation，那么就有一个 $G\to H$ 的同态了。如果替换出来的 H 元素能生成 H，那么是满射，额外的，如果 $G, H$ 大小相等，那就是同构。

1.7 群作用（group actions）

群 $G$ 作用在集合 $A$ 上是指一个从 $G\times A$ 到 $A$ 的映射（写作 $g\cdot a$），满足：

1. $g_1\cdot (g_2\cdot a)=(g_1g_2)\cdot a, \forall g_1, g_2\in G, a\in A$
2. $1\cdot a=a, \forall a\in A$

对于固定的 $g\in G$，定义 $\sigma_g: A\to A$ 为 $\sigma_g(a)=g\cdot a$，这是个排列（因为可以逆元 $\sigma_{g^{-1}}$）。并且，从 $G$ 到 $S_A$ 的映射 $g\to \sigma_g$ 是一个同态，这个同态称为作用的排列表示。

可以发现作用对应到一个排列表示，一个排列表示也能对应到一个作用，所以它们之间有双射关系。

这里都是左作用，也可以类似定义右作用。

如果 $ga=a$，那么所有排列都是恒等排列，这种作用是平凡的（trivial action）。

如果不同的 $g$ 对应的排列互不相同（也就是那个同态是单射），那么这种作用叫 faithful。

所有 $\sigma_g$ 是恒等排列的 $g$ 的集合是这个作用的核（kernel）。核是 $G$ 的子群。

等价关系 $\sim$：$a\sim b$ 当且仅当 $a=hb, \exist h\in G$。这个等价类称为 $a$ 的轨道。

拉格朗日定理：设 $H\leq G$，然后 $H$ 作用在 $G$ 上，设 $x\in G$，令 $\mathcal{O}$ 为 $x$ 的轨道，则映射 $H\to \mathcal{O}, h\to hx$ 是双射，从而可以证明 $|H|$ 是 $|G|$ 的约数。

二、子群

2.1 定义

群 $G$ 的子集 $H$，在二元运算和逆元下封闭，那么 $H$ 是 $G$ 的子群，记为 $H\leq G$。

判定子群：

1. $H$ 非空
2. $\forall x, y\in H, xy^{-1}\in H$

特别的，如果 $H$ 有限，那么第二个条件可以简单为仅检查运算封闭性。

2.2 中心化子（centralizer）、正规化子（normalizer）、稳定化子（stabilizer）、核（kernel）

中心化子：设 $A$ 是群 $G$ 的任意非空子集，$C_G(A)=\{g\in G \mid gag^{-1}=a, \forall a\in A\}$，这定义为 $A$ 在群 $G$ 的中心化子（也就是跟 $A$ 里所有元素 $a$ 有交换律的元素）。可以证明中心化子是 $G$ 的子群。

中心：定义 $Z(G)=\{g\in G \mid gx=xg, \forall x\in G\}$，即能与所有 $G$ 中元素满足交换律的集合，注意到 $Z(G)=C_G(G)$，所以 $Z(G)\leq G$。

正规化子：定义 $gAg^{-1}=\{gag^{-1} \mid a \in A\}$，那么正规化子就是 $N_G(A)=\{g\in G \mid gAg^{-1}=A\}$。同样可以证明 $N_G(A)\leq G$，以及 $C_G(A)\leq N_G(A)$。

稳定化子：设群 $G$ 作用在集合 $S$ 上，$s\in S$，则 $s$ 的稳定化子是集合 $G_s=\{g\in G \mid g\cdot s = s\}$。$G_s\leq G$。

事实上，中心化子、正规化子都是稳定化子、核的特例。定义共轭（conjugation）运算为上述形如 $gBg^{-1}$, $gbg^{-1}$ 的运算。设 $G$ 为群，$S=\mathcal{P}(G)$（$G$ 所有子集组成的集合），$G$ 作用在 $S$ 上，使用共轭运算。那么 $N_G(A)$ 就是 $A$ 的稳定化子，从而是 $G$ 的子群。接下来让群 $N_G(A)$ 作用在 $S=A$ 上，同样使用共轭运算，那么 $C_G(A)$ 就是这个作用的核。最后，$Z(G)$ 是 $G$ 作用在 $S=G$ 上，使用共轭运算，这个作用的核。

2.3 循环群

是指能由一个元素 $x$ 生成的群 $H=\{x^n \mid n\in \mathbb{Z}\}$，记作 $H=\langle x\rangle$。显然循环群都是阿贝尔群。

如果 $H=\langle x \rangle$，那么 $|H|=|x|$。（有限情况，证明 $1, x, x^2, \cdots, x^{n-1}$ 是互不相同的，无限情况，证明 $\forall a\neq b \in \mathbb{Z}, x^a\neq x^b$）

设 $G$ 是任意群，$x\in G, m, n\in \mathbb{Z}$，若 $x^n=x^m=1$，则 $x^d=1$ 其中 $d=(m, n)$（使用裴蜀定理可证）。特别的，如果 $x^m=1$ 那么 $|x| \mid m$。

任意两个同阶的循环群都同构。

对任意 $n\in \mathbb{Z}^+$，令 $Z_n$ 表示阶为 $n$ 的循环群。

令 $G=\langle x \rangle$，$a\in \mathbb{Z}-\{0\}$，则

1. 如果 $|x|=\infty$，那么 $|x^a|=\infty$（反证法）
2. 如果 $|x|=n<\infty$，那么 $|x^a|=\frac{n}{(n, a)}$（反复设一些量就可以证明）

设 $H=\langle x \rangle$，那么

1. 如果 $|x|=\infty$，那么 $H=\langle x^a \rangle$ 当且仅当 $a=\pm 1$
2. 如果 $|x|=n<\infty$，那么 $H=\langle x^a \rangle$ 当且仅当 $(a, n)=1$，特别的，能生成 $H$ 的生成元有 $\varphi(n)$ 个。

设 $H=\langle x \rangle$，

1. $H$ 的任意子群都是循环群，若 $K\leq H$，要么 $K=\{1\}$，要么 $K=\langle x^d \rangle$ 其中 $d$ 是最小正整数满足 $x^d\in K$
2. 如果 $|H|=\infty$，那么对于任意非负整数 $a\neq b$，$\langle x^a \rangle\neq \langle x^b \rangle$，另外 $\langle x^m\rangle=\langle x^{|m|} \rangle$
3. 如果 $|H|=n<\infty$，那么对于任意正整数 $a|n$，有唯一阶为 $a$ 的子群 $\langle x^d\rangle, d=\frac{n}{a}$。另外 $\langle x^m\rangle=\langle x^{(n, m)} \rangle$

2.4 由子集生成的子群

子群的交也是子群。设 $A$ 是群 $G$ 的任意子集，定义 $\langle A\rangle = \bigcap_{A\subseteq H, H\leq G}H$，称为由 $A$ 生成的子群。

定义 $\overline{A}=\{a_1^{\epsilon_1}a_2^{\epsilon_2}\cdots a_n^{\epsilon_n} \mid n\in \mathbb{Z}, n\geq 0, a_i\in A, \epsilon_i=\pm 1\}$，那么 $\overline{A}=\langle A\rangle$。

当然，这里 $\overline{A}$ 的定义也可以把相邻相同 $a_i$ 合并起来。如果 $G$ 是阿贝尔群，那么可以把所有相同的 $a_i$ 合并起来，如果在此基础上每个 $a_i$ 有一个有限的阶 $d_i$，可以知道 $|\langle A \rangle|\leq d_1d_2\cdots d_k$。

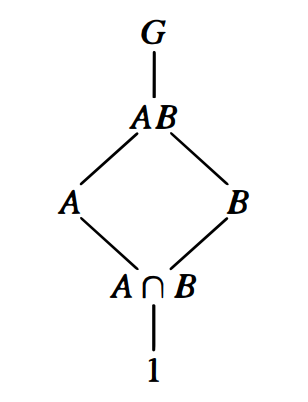
2.5 子群的图状结构

可以把子群写成一个 DAG，最上面是群 $G$，最下面是只有单位元的群，阶数大的群靠上，然后两个子群之间如果有包含关系、中间没有包含其他子群，则连边。

三、商群（quotient group）与同态

3.1 定义

对于一个映射与像集里的一个元素，定义这个元素的 fiber 为所有映射到这元素的原像组成的集合。

设 $\varphi: G\to H$ 是同态，那么 $\varphi$ 的核是 $\{g\in G \mid \varphi(g)=1\}$，记作 $\ker \varphi$

性质：

1. $\varphi(1_G)=1_H$（$\varphi(1_G)=\varphi(1_G1_G)=\varphi(1_G)\varphi(1_G)$，使用消去律）
2. $\forall g\in G, \varphi(g^{-1})=\varphi(g)^{-1}$
3. $\forall n\in \mathbb{Z}, \varphi(g^n)=\varphi(g)^n$
4. $\ker\varphi\leq G$
5. $\mathrm{im}(\varphi)\leq H$（这是 $G$ 在 $\varphi$ 下的像）

设 $\varphi: G\to H$ 是同态，核是 $K$，商群 $G/K$ 是 $\varphi$ 的所有 fiber 组成的群，$a, b$ 的 fiber 的乘积定义为 $ab$ 的 fiber。

性质：设 $X\in G/K$ 是 $a$ 的 fiber，即 $X=\varphi^{-1}(a)$，那么

1. $\forall u\in X, X=\{uk \mid k\in K\}$（先证 $uK\subseteq X$，再证反过来）
2. $\forall u\in X, X=\{ku \mid k\in K\}$

设 $N\leq G$，对任意 $g\in G$，定义 $gN=\{gn \mid n\in N\}$ 为一个 $G$ 的左陪集（left coset），同样定义右陪集。任何陪集里的元素称为这个陪集的代表元（representative）。注意到 $N$ 在 $G$ 的作用，一个轨道其实就是一个右陪集。

设 $G$ 是群，$K$ 是一个 $G$ 到其他群的同态的核，那么 $K$ 的左陪集集合构成群，运算是 $uK\circ vK=(uv)K$。并且这是良定义的。右陪集同理。

设 $G$ 是群，$N$ 是任意子群，那么 $N$ 的所有左陪集可以把 $G$ 分割（任意两个不同左陪集没有交集、可以组成整个 $G$）。并且，$uN=vN$ 当且仅当 $v^{-1}u\in N$ 当且仅当 $u, v$ 是同一个陪集的代表元。

设 $G$ 是群，$N$ 是子群

1. 在 $N$ 的左陪集上定义的运算 $uN\cdot vN=(uv)N$ 是良定义的当且仅当 $\forall g\in G, n\in N, gng^{-1}\in N$
2. 如果是良定义的，那么这些左陪集构成一个群，单位元是 $1N$，逆元是 $(gN)^{-1}=g^{-1}N$

元素 $gng^{-1}$ 是 $n\in N$ 通过 $g$ 的共轭，$gNg^{-1}=\{gng^{-1}\mid n\in N\}$ 是 $N$ 通过 $g$ 的共轭。元素 $g$ 正规化 $N$ 是指 $gNg^{-1}=N$。一个子群 $N$ 是正规子群当且仅当 $G$ 的所有元素都正规化 $N$，此时记作 $N\unlhd G$

综上所述，以下等价：

1. $N\unlhd G$
2. $N_G(N)=G$
3. $\forall g\in G, gN=Ng$
4. 定义在 $N$ 的左陪集上的上述运算构成群
5. $\forall g\in G, gNg^{-1}\subseteq N$

判断正规子群比较麻烦，如果知道 $G$ 或者 $N$ 的生成元都可以简化运算。

$N$ 是 $G$ 的正规子群当且仅当 $N$ 是某个同态的核。（如果是核，那么左陪集和右陪集相同，$gN=Ng$，就正规；如果正规，构造同态 $\pi: G\to G/N$, $\forall g\in G, \pi(g)=gN$，这个同态称为自然同态）

3.2 拉格朗日定理

设 $G$ 是有限群，$H$ 是 $G$ 的子群，则 $|H| \mid |G|$，$H$ 的左陪集数量是 $\frac{|G|}{|H|}$

$H$ 的左陪集数量称为 $H$ 在 $G$ 里的 index，记作 $|G:H|$

设 $G$ 是有限群，$x\in G$，$x$ 的阶是 $G$ 的阶的约数，并且 $x^{|G|}=1$

如果 $G$ 是阶为质数 $p$ 的有限群，那么 $G$ 是循环群，$G\cong Z_p$

柯西定理：设 $G$ 是有限群，质数 $p$ 整除 $|G|$，那么 $G$ 存在阶为 $p$ 的元素。

一种证明见下图，另一种证明不在这一章。

Sylow 定理：设 $G$ 是阶为 $p^{\alpha}m$ 的有限群，其中 $p$ 是质数，不整除 $m$，那么 $G$ 有阶为 $p^{\alpha}$ 的子群。

证明不在这一章。

设 $H, K$ 是一个群的子群，定义 $HK=\{hk \mid h\in H, k\in K\}$

如果 $H, K$ 都是有限群则 $|HK|=\frac{|H||K|}{|H\cap K|}$。证明就是要说明 $K$ 的在 $H$ 内的不同左陪集数量，跟 $H\cap K$ 的在 $H$ 内的不同左陪集数量相同。

如果 $H, K$ 都是子群，那么 $HK$ 是子群当且仅当 $HK=KH$

如果 $H, K$ 是 $G$ 的子群，$H\leq N_G(K)$，那么 $HK$ 是 $G$ 的子群。特别的，如果 $K\unlhd G$ 那么 $\forall H\leq G, HK\leq G$

如果 $A$ 是 $N_G(K)$（$C_G(K)$）的子集，那么说 $A$ 正规化（中心化）$K$

3.3 同构定理

第一同构定理：设 $\varphi: G\to H$ 是同态，那么 $\ker \varphi \unlhd G$ 且 $G/\ker \varphi \cong \varphi(G)$

推论：$\varphi$ 是单射当且仅当 $\ker\varphi=1$，$|G : \ker\varphi|=|\varphi(G)|$

第二同构定理：设 $G$ 是群，$A, B$ 是子群，$A\leq N_G(B)$，那么 $AB$ 是 $G$ 的子群，$B\unlhd AB$，$A\cap B\unlhd A$，$AB/B\cong A/A\cap B$

也称为钻石同构定理，原因如下图

第三同构定理：$G$ 是群，$H, K$ 是正规子群，$H\leq K$，那么 $K/H\unlhd G/H$ 且 $(G/H)/(K/H)\cong G/K$

第四同构定理：$G$ 是群，$N\unlhd G$，那么在包含 $N$ 的子群 $A$ 与 $G/N$ 的子群 $\overline{A}=A/N$ 有双射关系。对于任意 $A, B\leq G, N\leq A, N\leq B$：

1. $A\leq B$ 当且仅当 $\overline{A}\leq \overline{B}$
2. 如果 $A\leq B$ 那么 $|B:A|=|\overline{B}:\overline{A}|$
3. $\overline{\langle A, B \rangle}=\langle \overline{A}, \overline{B} \rangle$
4. $\overline{A\cap B}=\overline{A}\cap \overline{B}$
5. $A\unlhd G$ 当且仅当 $\overline{A}\unlhd \overline{G}$

3.4 合成列

一个群 $G$，如果只有 $1$ 和 $G$ 两个正规子群，那么它叫做单群（simple group）

在群 $G$ 中，一个子群序列 $1=N_0\leq N_1 \leq N_2 \leq \cdots \leq N_{k-1} \leq N_k=G$ 是合成列（composition series），当且仅当 $N_i\unlhd N_{i+1}$，$N_{i+1}/N_i$ 是单群。每一个 $N_{i+1}/N_i$ 是 $G$ 的合成因子（composition factor）

Jordan-Holder 定理：设 $G\neq 1$ 是有限群，那么 $G$ 存在合成列，且合成列唯一。唯一是指如果 $1=N_0\leq N_1\leq \cdots \leq N_r=G$，$1=M_0\leq M_1\leq \cdots \leq M_s=G$，那么 $r=s$，且存在 $\{1, 2, \cdots, r\}$ 排列 $\pi$ 满足 $M_{\pi(i)}/M_{\pi(i)-1}\cong N_i/N_{i-1}$

【The Holder Program 还没看】

3.5 对换与交错群

在置换里，一个长度为 2 的环是一个对换（transposition）

设 $x_1, \cdots, x_n$ 是独立变量且 $\Delta=\prod_{1\leq i<j \leq n} (x_i - x_j)$。对于排列 $\sigma$，定义 $\sigma(\Delta)=\prod_{1\leq i<j \leq n} (x_{\sigma(i)}-x_{\sigma(j)})$，当 $\sigma(\Delta)=+\Delta$ 时排列为偶排列，$\epsilon(\sigma)=1$，当 $\sigma(\Delta)=-\Delta$ 时排列为奇排列，$\epsilon(\sigma)=-1$。这个 $\epsilon$ 是 $S_n$ 到 $\{\pm 1\}$（运算为乘法）的同态。

长度为 $n$ 的交错群（alternating group），记作 $A_n$，是 $\epsilon$ 的核（所有偶排列）

四、群作用

4.1 群作用与排列表示

群 $G$ 作用在集合 $A$ 上，核是指作用所有集合元素都到自己的群内元素，稳定化子是指作用这个集合元素到自己的群内元素，作用是 faithful 是指核只有一个。

$\varphi: G\to S_A, \varphi(g)=\sigma_g$，是一个同态，意味着群作用的核是 $G$ 的正规子群。

对于任意群 $G$ 和集合 $A$，$G$ 在 $A$ 上的作用与 $G$ 到 $S_A$ 的同态是双射关系。

等价关系 $\sim$：$a\sim b$ 当且仅当 $a=gb, \exist g\in G$。这个等价类称为 $a$ 的轨道。$a$ 的轨道大小等于 $a$ 的稳定化子的 index $|G:G_a|$（证明考虑构造映射 $b=ga\to gG_a$，这是双射）

如果作用只有一个轨道，那么这个作用是 transitive 的。

用群作用的方法可以证明一个排列 $\sigma$ 有唯一环分解，使用对称群的循环子群 $\langle \sigma \rangle$ 在 $\{1, 2, \cdots, n\}$ 的作用的轨道来证明。

4.2 通过左乘作用到自身的群作用、Cayley 定理

这种群作用的定义如标题。

设 $G$ 是群，$H\leq G$，$A$ 是 $H$ 的左陪集集合，$G$ 通过左乘作用在 $A$ 上，设 $\pi_H$ 是对应排列表示，那么

1. 这个作用 transitive
2. $1H\in A$ 的稳定化子是子群 $H$
3. 作用的核（也是 $\pi_H$ 的核）是 $\bigcap_{x\in G} xHx^{-1}$，且这个核 $\ker \pi_H$ 是 $G$ 的最大的被 $H$ 包含的正规子群

Cayley 定理：任何群都同构于某个对称群的子群，如果群 $G$ 的阶为 $n$，那么 $G$ 同构于 $S_n$ 的一个子群。（证明：在上个定理里令 $H=1$，得到一个从 $G$ 到 $S_G$ 的同态）

设 $G$ 是阶为 $n$ 的有限群，$p$ 是最小的整除 $|G|$ 的质数，那么任何 index 为 $p$ 的子群都是正规子群。（任取 index 为 $p$ 的子群 $H$，考虑 $G$ 左乘作用在 $H$ 的左陪集集合的排列表示 $\pi_H$，$K=\ker \pi_H$，通过 $G/K$ 同构于 $S_p$ 的子群证明 $H=K$）

4.3 通过共轭作用到自身的群作用

定义如标题 $g\cdot a=gag^{-1}$。两个 $G$ 中元素 $a, b$ 称为共轭的当且仅当 $\exist g\in G, b=gag^{-1}$。这种群作用的轨道称为共轭类。

同样可以扩展作用的集合，$G$ 可以通过共轭作用到 $\mathcal{P}(G)$ 上（$G$ 的所有子集构成的集合），$g\cdot S=gSg^{-1}$。同样可以定义两个子集的共轭关系。

通过前述结论可知，对于群 $G$ 的子集 $S$，其稳定化子是 $G_S=N_G(S)$，则与 $S$ 共轭的子集数量 等于 $|G:N_G(S)|$。特别的，与元素 $s$ 共轭的元素数量就是 $|G:C_G(s)|$

类方程（the class equation）：设 $G$ 是有限群，$g_1, \cdots, g_r$ 是 $G$ 的所有不被中心 $Z(G)$ 包含的共轭类的代表元，那么 $|G|=|Z(G)|+\sum_{i=1}^r|G:C_G(g_i)|$

设 $p$ 是质数，$P$ 是阶为 $p^\alpha$ 的群，那么 $Z(P)\neq 1$。由类方程可以直接得到。

推论：如果 $|P|=p^2$，那么 $P$ 是阿贝尔群，并且 $P$ 同构于 $Z_{p^2}$ 或 $Z_p\times Z_p$

对称群 $S_n$ 里的共轭：设 $\sigma, \tau\in S_n$，$\sigma$ 的环分解是 $(a_1~a_2~\cdots~a_{k_1})~(b_1~b_2~\cdots~b_{k_2})~\cdots$，那么 $\tau\sigma\tau^{-1}$ 的环分解是 $(\tau(a_1)~\tau(a_2)~\cdots~\tau(a_{k_1}))~(\tau(b_1)~\tau(b_2)~\cdots~\tau(b_{k_2}))~\cdots$

设 $\sigma\in S_n$ 的环长为 $n_1\leq n_2\leq \cdots\leq n_r$（包括长度为 $1$ 的环），定义 $n_1, n_2, \cdots, n_r$ 为 $\sigma$ 的 cycle type；对于 $n\in \mathbb{Z}^+$，$n$ 是 partition 是任何和为 $n$ 的不降正整数序列。

两个排列共轭当且仅当它们的 cycle type 一样。

使用共轭可以证明一些东西。首先观察到如果 $H\unlhd G$，那么对于任何 $G$ 的共轭类 $K$ 都有要么 $K\subseteq H$ 要么 $K\cap H=\varnothing$。然后通过一堆有点复杂的讨论可以证明出 $A_5$ 是单群。

4.4 自同构

设 $G$ 是个群，一个从 $G$ 到自身的同构叫做自同构（automorphism），$G$ 的所有自同构组成的集合记作 $Aut(G)$（事实上，在映射复合运算下，这是个群，可以看作 $S_G$ 的子群）

如果 $H\unlhd G$，那么 $G$ 的每个元素以共轭运算作用到 $H$ 上都是一个自同构（$h\to ghg^{-1}$）。这个作用的排列表示是一个到 $Aut(H)$ 的同态，核是 $C_G(H)$，$G/C_G(H)$ 同构于 $Aut(H)$ 的一个子群。

设 $K\leq G, g\in G$，那么 $K\cong gKg^{-1}$，共轭元素和共轭子群有同样的阶。

设 $K\leq G$，商群 $N_G(H)/C_G(H)$ 同构于 $Aut(H)$ 的一个子群。特别的，$G/Z(G)$ 同构于 $Aut(G)$ 的一个子群。

设 $G$ 是群，$g\in G$，由 $g$ 的共轭得到的自同构称为内自同构，$G$ 的所有内自同构组成的群是 $Aut(G)$ 的一个子群，记作 $Inn(G)$，$Inn(G)\cong G/Z(G)$

群 $G$ 的子群 $H$ 如果满足 $\forall \sigma\in Aut(G)$, $\sigma(H)=H$，那么 $H$ 称为 $G$ 的特征子群，记作 $H$ char $G$

一些特征子群的性质：

1. 特征子群都是正规子群
2. 如果 $H$ 是一个阶的唯一 $G$ 子群，那么 $H$ char $G$
3. 如果 $K$ char $H$ 且 $H\unlhd G$，那么 $K\unlhd G$

阶为 $n$ 的循环群的自同构群同构于 $(\mathbb{Z}/n\mathbb{Z})^\times$（一个阶为 $\varphi(n)$ 的阿贝尔群）

例子：设 $G$ 是阶为 $pq$ 的群，其中 $p, q$ 是质数，$p\leq q$，$p\not\mid q-1$，则 $G$ 是阿贝尔群

• 若 $Z(G)\neq 1$，则由拉格朗日定理知 $G/Z(G)$ 是循环群，从而可证 $G$ 是阿贝尔群
• 若 $Z(G)=1$，若每个非单位元的阶都是 $p$，那么每个非单位元的中心化子阶都是 $q$（不能再大了），由类方程知 $pq=1+kq$，不可能成立；若元素 $x$ 的阶为 $q$，设 $H=\langle x \rangle$，则由于 $H$ 的 index 为 $p$ 且 $p$ 是 $G$ 的最小质因数，可得 $H$ 是正规子群，再由于 $C_G(H)=H$（不能再大了），可知 $G/H=N_G(H)/C_G(H)$ 是阶为 $p$ 的子群，同构于 $Aut(H)$ 的一个子群，但 $Aut(H)$ 的阶应为 $\varphi(q)=q-1$，与条件矛盾。最终可知 $G$ 是阿贝尔群。

一些性质：

1. 如果 $p$ 是奇质数，$n\in \mathbb{Z}^+$，那么阶为 $p$ 的循环群的自同构群的阶为 $p-1$，阶为 $p^n$ 的循环群的自同构群的阶为 $p^{n-1}(p-1)$
2. $\forall n\geq 3$，阶为 $2^n$ 的循环群的自同构群同构于 $Z_2\times Z_{2^{n-2}}$，这不是循环群但是有 index 为 $2$ 的子群（这里没太懂，有没有好心人教教）
3. 设 $p$ 是质数，$V$ 是阿贝尔群（运算用加法表示），具有性质 $\forall v\in V, pv=0$，如果 $|V|=p^n$，那么 $V$ 是数域 $\mathbb{F}_p$ 下的 $n$ 维向量空间。$V$ 的自同构群就是所有满秩线性变换，满足 $Aut(V)\cong GL(V)\cong GL_n(\mathbb{F}_p)$
4. $\forall n\neq 6$, $Aut(S_n)=Inn(S_n) \cong S_n$。对于 $n=6$ 有 $|Aut(S_6):Inn(S_6)|=2$
5. $Aut(D_8)\cong D_8$, $Aut(Q_8)\cong S_4$

4.5 Sylow 定理

设 $p$ 为质数，阶为 $p^\alpha$（$\alpha\geq 1$）的群称为 $p$ 群，阶满足这个的子群叫 $p$ 子群。若 $G$ 的阶为 $p^\alpha m$，其中 $p\not\mid m$，那么 $G$ 的阶为 $p^\alpha$ 的子群称为 $G$ 的 Sylow $p$ 子群。$G$ 的 Sylow $p$ 子群的集合记作 $Syl_p(G)$，数量记作 $n_p(G)$

Sylow 定理：设 $G$ 是阶为 $p^\alpha m$ 的群，其中 $p$ 是质数，不整除 $m$，则

1. Sylow $p$ 子群存在，即 $Syl_p(G)\neq \varnothing$
2. 若 $P$ 是 $G$ 的 Sylow $p$ 子群，$Q$ 是 $G$ 的任意 $p$ 子群，则存在 $g\in G$ 满足 $Q\leq gPg^{-1}$。特别的，任意两个 Sylow $p$ 子群共轭
3. $G$ 的 Sylow $p$ 子群数量形如 $1+kp$，即 $n_p\equiv 1\pmod p$。对任意 Sylow $p$ 子群 $P$，$n_p$ 是 $N_G(P)$ 在 $G$ 中的 index，因此 $n_p\mid m$

引理：设 $P\in Syl_p(G)$，$Q$ 是 $G$ 的任意 $p$ 子群，那么 $Q\cap N_G(P)=Q\cap P$（证明设 $H=N_G(P)\cap Q$，显然 $P\cap Q\leq H$，$H\leq Q$，所以只要证明 $H\leq P$。通过说明 $PH$ 是 $G$ 的 $p$ 子群，包含了 $P$ 和 $H$，而 $P$ 是阶最大的 $p$ 子群，所以 $PH=P$，$H\leq P$）

证明 Sylow 定理的 1：归纳，然后分 $p\mid |Z(G)|$ 和 $p\not\mid |Z(G)|$ 讨论，前者根据柯西定理取 $Z(G)$ 的一个阶为 $p$ 的子群 $N$ 来获得商群 $G/N$，使用归纳假设，后者根据类方程得知存在 $|C_G(g_i)|=p^\alpha k$，使用归纳假设得到它的 Sylow $p$ 子群（显然也是 $G$ 的）

要证明 2、3，先计算一个东西：设 $P$ 是 $G$ 的任一 Sylow $p$ 子群，令 $\mathcal{S}=\{P_1, P_2, \cdots, P_r\}$ 是 $P$ 的所有共轭。设 $Q$ 是任一 $p$ 子群，$Q$ 可以作用在 $\mathcal{S}$ 上，假设有 $s$ 个轨道 $\mathcal{S}=\mathcal{O}_1\cup \mathcal{O}_2 \cup \cdots \cup \mathcal{O}_s$，注意 $s$ 会因 $Q$ 的选择而变化，但 $r=|\mathcal{O}_1|+\cdots +|\mathcal{O}_s|=|\mathcal{S}|$ 是固定的。假设 $P_i\in \mathcal{O}_i$，显然 $|\mathcal{O}_i|=|Q:N_Q(P_i)|$，根据 $N_Q(P_i)=N_G(P_i)\cap Q$ 和上述引理，可知 $|\mathcal{O}_i|=|Q:P_i\cap Q|$。最后我们通过一个简单的计算得到 $r\equiv 1\pmod p$，取 $Q=P_1$，则 $|\mathcal{O}_1|=1$，而 $p$ 能整除其他 $|\mathcal{O}_i|$。

证明 2：反证，假设 $Q$ 不被 $\mathcal{S}$ 的任何集合包含，那么 $|\mathcal{O}_i|=|Q:Q\cap P_i|>1$，被 $p$ 整除，与 $r$ 的余数矛盾。后面的“特别的”直接让 $Q$ 取 Sylow $p$ 子群即可。

证明 3：前半已可直接看出，后半再注意到 $n_p=|G:N_G(P)|$ 即可。

推论：设 $P$ 是 $G$ 的一个 Sylow $p$ 子群，则以下等价

1. $P$ 是 $G$ 的唯一 Sylow $p$ 子群
2. $P$ 是 $G$ 的正规子群
3. $P$ 是 $G$ 的特征子群
4. 设 $X$ 是 $G$ 的子集满足 $\forall x\in X$，$x$ 的阶是 $p$ 的次幂，则 $\langle X \rangle$ 是 $p$ 子群