普通物理预习笔记

做点记录以免以后遗忘。

一、基础内容

多元微积分相关内容，这里先不写了。

二、运动学

极坐标有时有用。

 

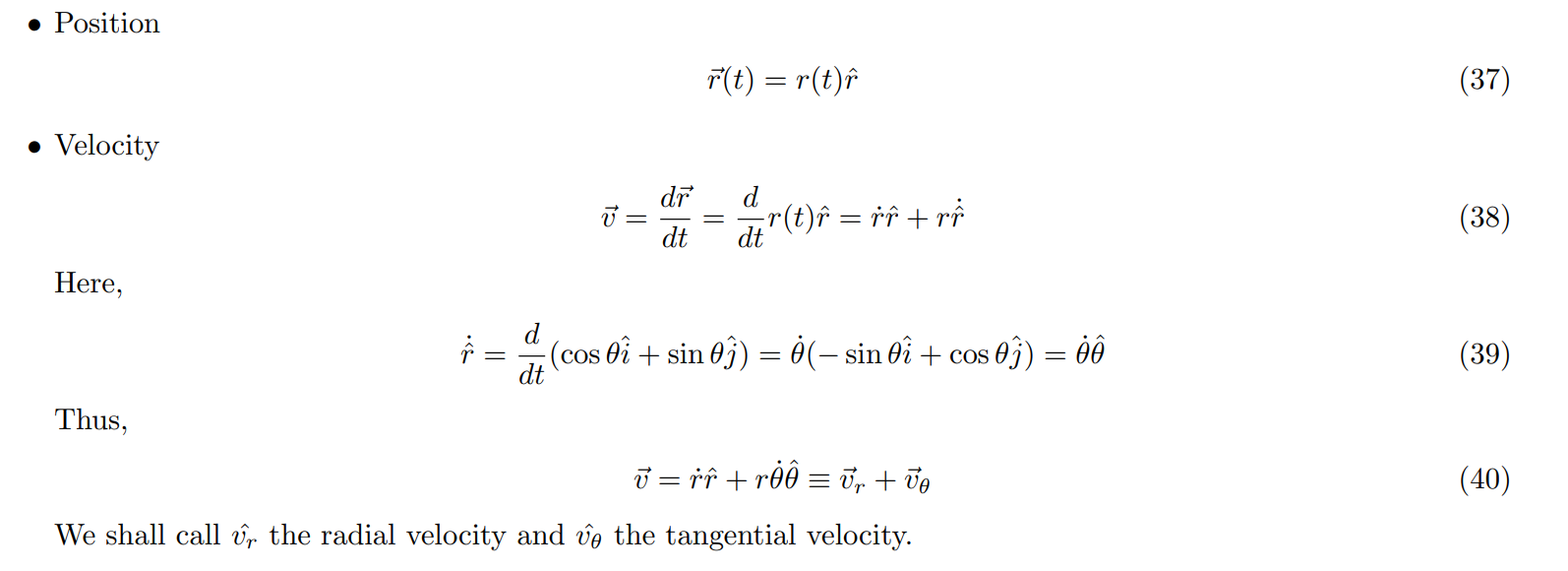
角速度是矢量，角位移不是。使用角速度的时候可以引入一条垂直于平面的 z 轴。

三、牛顿运动定律

首先，牛顿运动定律只能在惯性系下成立，非惯性系下要引入惯性力才行。

$\vec{F}_a=-m\vec{a}_0$，然后 $m\vec{a}'=\vec{F}+\vec{F}_a$

再看一种特殊的非惯性参考系：旋转非惯性参考系（有着角速度 $\omega$）。

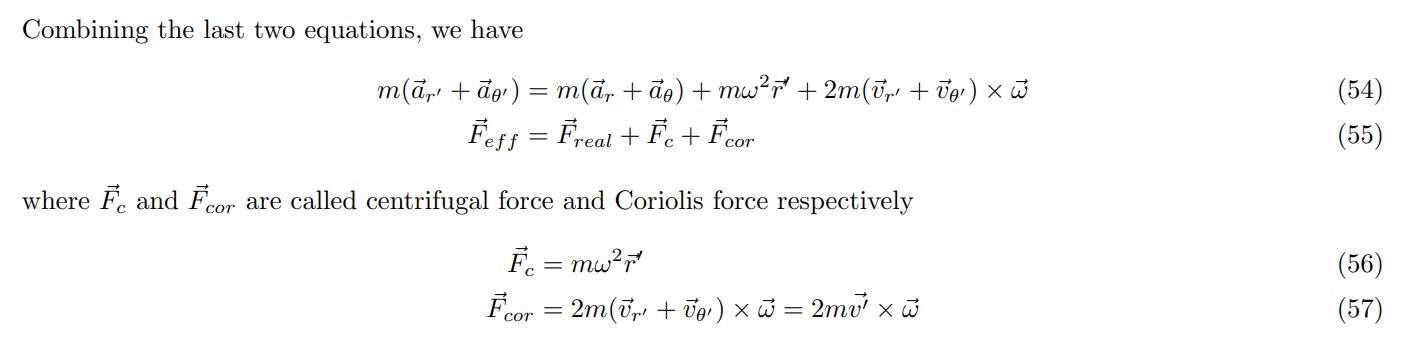
最后能得到的是两个方向的惯性力，前者是离心力，可以用一个匀速圆周运动来理解，后者是科里奥利力，以匀速自转的地球上为参考系，它就是地转偏向力。

四、动量

$$\vec{p}=m\vec{v}$$

根据牛顿第二定律，力是动量对时间的导数。可以把一堆东西看成整体计算动量，如果没有外力那动量守恒。

造火箭：燃料以相对于火箭 $\vec{u}=-u\vec{i}$ 的速度喷出，火箭速度 $v(t)\vec{i}$，火箭质量 $m_r(t)$，在 $t$ 时刻喷出的燃料质量 $dm_f=-dm_r$，外力 $F_{ext}$。利用微元分析的方法，分析时刻 $t$ 和 $t+dt$ 的动量差，从而得到导数，再根据外力来解方程（积个分）。

最后结果：无外力情况下，$v_f-v_i=u\ln\left(\frac{m_{r, i}}{m_{r, f}}\right)$，这解释了为什么要多级火箭；有恒定重力 $\vec{g}$ 的情况，$v_f-v_i=u\ln\left(\frac{m_{r, i}}{m_{r, f}}\right)-gt$，其中 $t$ 是从 $i$ 到 $f$ 的持续时间，这解释了为什么要尽快把燃料烧完。

质心，按质量为权重算位置的带权平均数。质心的速度，也按质量为权重。质心的动量是所有动量的和，也是总质量乘质心的速度。加速度跟速度一样。外力是总质量乘质心加速度。

质心参考系（COM 系），让质心处于原点、速度为零、动量为零。

在二体问题中，可以以一个物体为参考系，让一个物体不动，另一个物体动。由于这很可能是非惯性系，不满足牛顿第二定律，所以引入惯性力，可以解出一个约化质量 $\mu$ 满足 $\frac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2}$。

五、能量和功

能量和功基本是些高中内容。注意在 COM 系和另一个参考系 S 中，假设 COM 系相对于 S 速度为 $\vec{u}$，那么 S 系下的动能是 COM 系的动能加上总质量、速度 $\vec{u}$ 的动能。

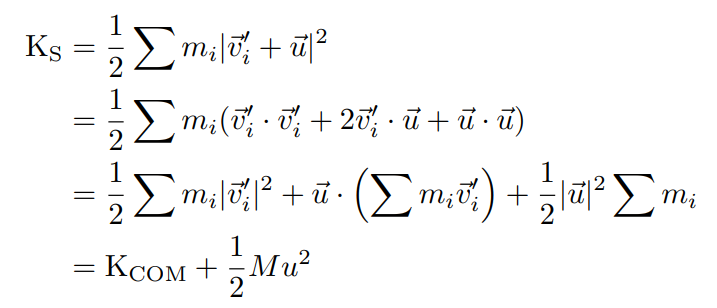
势能，首先从保守力开始（类似于保守场，积分跟路径无关，这里就是功与路径无关），例子有重力、弹力、万有引力，那么势能的变化其实就是保守力做的功的负数。

势能函数，可以看出哪些点受力为 0（导数为 0），然后稳定还是不稳定看二阶导数（正是稳定，负是不稳定）。

引力势能 $U_g(r)=-Gm_Am_B\frac{1}{r}$，可以用于计算逃逸速度。

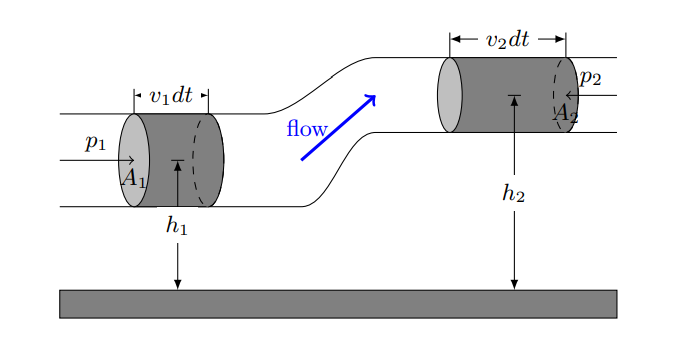
伯努利方程，用于计算理想流体的一些性质：

$$\frac{p}{\rho g}+\frac{v^2}{2g}+h=constant$$

推导方法是机械能守恒，压力做的功 = 机械能变化量

热力学第一定律（能量守恒）。

六、角动量

一个质量为 $m$ 的质点速度为 $\vec{v}$，动量为 $\vec{p}=m\vec{v}$，关于点 $S$ 的角动量为 $\vec{L}_S=\vec{r}_S\times \vec{p}$

力矩就是角动量的导数，可以发现让叉积左边的导之后会导出来速度从而变成 $0$，因此只有叉积右边导的那一项，也就是 $\vec{r}_S\times \vec{F}=\vec{M}_S$，形式上跟动量导数是力很接近。

开普勒第二定律：行星绕太阳运动，行星与太阳的连线在同样长度的时间内扫过的面积相等，可以用角动量守恒来解释。

COM 系下，角动量一样定义为和，力矩显然也是，考虑内部的力都是在两个点之间的方向上，那么内部的力矩是零。如果外部的力矩是零，那么角动量守恒。

一些点组成的系统，关于不同点 $A, B$ 的角动量关系为 $\vec{L}_A=\vec{L}_B+\vec{r}_{A, B}\times \vec{p}_{sys}$，因此如果一个系统的动量为零，那么关于任何点的角动量是一样的。COM 系就是一个例子。

COM 系下，惯性力的力矩为零，角动量有如下关系 $\vec{L}=\vec{L}'+\vec{r}_C\times \vec{p}_C$

七、碰撞

使用两个物体相对速度来描述碰撞。碰撞系数 $e=\frac{v_B}{v_h}$（分子是最终相对速度，分母是初始相对速度）。如果 $e=1$ 则动能不变，是弹性碰撞。如果 $e<1$ 则动能变小，是非弹性碰撞。如果 $e=0$ 则为完全非弹性碰撞（直接贴贴在一起了），动能变化量 $\Delta K=-\frac{1}{2}\mu v_h^2=-\frac{1}{2}\frac{m_1m_2}{m_1+m_2}v_h^2$。如果 $e>1$ 则是超弹性碰撞。

考虑只有 x 轴，弹性碰撞，动量、能量守恒，可以解得

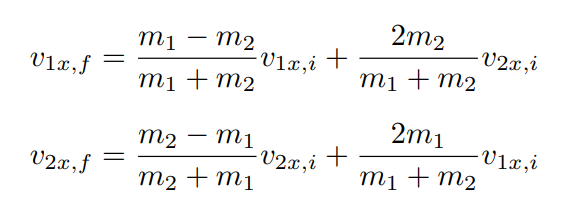
二维情况下，两个质量相等的质点，一开始一个静止，一个运动，然后发生弹性碰撞，碰撞后两者呈直角。

八、刚体

刚体是指在运动中和受力作用后，形状和大小不变，而且内部各点的相对位置不变的物体。

角速度向量，满足交换律，是矢量。

刚体的瞬时运动可以看作是一个位移加上一个旋转。

圆形的轮子在转动、平移时的情况（skidding 外侧滑，slipping 内侧滑）：

转动惯量：描述刚体绕轴转动时惯性的量度，从质点开始理解，质点中 $I=mR^2$，然后其余的本质上就是积分 $\int r^2dm$。

$L=I\omega, M=I\alpha$，描述了角动量与角速度、力矩与角加速度之间的关系。

平行轴定理：设刚体质量为 $m$，绕通过质心转轴的转动惯量为 $I_{cm}$，那么把这个轴平移距离 $d$，则绕新轴的转动惯量为 $I=I_{cm}+md^2$。

刚体同样有角动量守恒定律。

推导得到刚体的动能 $K=\frac{1}{2}I\omega^2$，力在旋转运动做的功就是 $\int Md\theta$

九、机械振动

简谐运动 $x(t)=A\cos(\omega t+\phi_0)$，常用关系式 $F=-m\omega^2x$, $k=m\omega^2$, $\omega=\sqrt{\frac{k}{m}}$, $T=2\pi \sqrt{\frac{m}{k}}=\frac{2\pi}{\omega}$, $f=\frac{1}{T}=\frac{\omega}{2\pi}$

从能量的角度分析，$E=K+U=\frac12 m\dot{q}^2+\frac12 kq^2$，可以知道在做 $\omega=\sqrt{\frac{k}{m}}$ 的简谐运动。

如果可以写成 $E(q, \dot{q})=\frac12 f(q)\cdot \dot{q}^2+V_{eff}(q)$，其中 $V_{eff}(q_0)=0, V'_{eff}(q_0)=0, V''_{eff}(q_0)>0$，可知 $q=q_0$ 是稳定点，在此处做二阶泰勒展开 $E(q, \dot{q})\approx \frac12 f(q)\cdot \dot{q}^2+\frac12 V''_{eff}(q_0)\cdot (q-q_0)^2$，于是简谐运动满足 $\omega=\sqrt{\frac{f(q_0)}{V''_{eff}(q_0)}}$

扭摆（torsion pendulum）：回复力矩是 $\tau=-\kappa\theta$，其中 $\kappa$ 是扭转系数（常量），模仿简谐运动，这个角简谐运动的周期为 $T=2\pi\sqrt{\frac{I}{\kappa}}$

摆：在角度较小的时候看作简谐运动，$T=2\pi\sqrt{\frac{I}{mgh}}$

简谐运动的组合

相同方向、相同频率：$x_1=A_1\sin \omega t$, $x_2=A_2\sin(\omega t+\phi)$, $x=A_1\sin \omega t+A_2\sin(\omega t+\phi)=A\sin(\omega t+\theta)$ 其中 $\tan\theta=\frac{A_2\sin\phi}{A_1+A_2\cos\phi}$, $A=\sqrt{A_1^2+A_2^2+2A_1A_2\cos\phi}$，可以用圆周运动理解

相同方向、不同频率、同样振幅：和差化积

垂直方向、相同频率：$x=A\cos \omega_x t$, $y=B\cos (\omega_y t+\phi)$，其中 $\omega_x=\omega_y=\omega$，对 $y$ 使用和角公式拆开，与 $x$ 进行消去，最后得到 $\frac{x^2}{A^2}+\frac{y^2}{B^2}-\frac{2xy\cos\phi}{AB}=\sin^2\phi$，相位差 $\phi$ 为 $0$ 时是条斜率为 $B/A$ 的直线，为 $\pi/2$ 时是椭圆。

垂直方向、不同频率：根据 $\omega_x/\omega_y$ 的比值有不同的曲线，如果比值是有理数那么是封闭曲线。

阻尼振动有三种情况：欠阻尼、过阻尼、临界阻尼，是根据二阶微分方程的判别式得到的分类。

受迫振动和共振